题目链接：所有路径

题目：

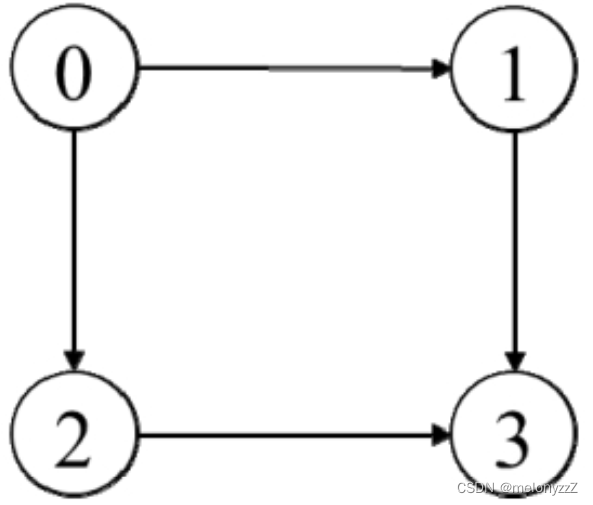
一个有向无环图由 n 个节点（标号从 0 到 n - 1，n >= 2）组成，请找出从节点 0 到节点 n - 1 的所有路径。图用一个数组 graph 表示，数组的 graph[i] 包含所有从节点 i 能直接到达的节点。例如，输入数组 graph 为 [[1, 2], [3], [3], []]，则输出两条从节点 0 到节点 3 的路径，分别为 0->1->3 和 0->2->3，如下图所示。

分析：

由于题目要求列出所有从节点 0 到节点 n - 1 的所有路径，因此采用深度优先搜索。

深度优先搜索通常用递归实现。从节点 0 出发开始搜索。每当搜索到节点 i 时，先将该节点添加到路径中去。如果该节点正好是节点 n - 1，那么就找到了一条从节点 0 到节点 n - 1 的路径。如果不是，则从 graph[i] 找到每个相邻的节点并用同样的方法进行搜索。当从节点 i 出发能够抵达的所有节点都搜索完毕之后，将回到前一个节点搜索其他与之相邻的节点。在回到前一个节点之前，需要将节点 i 从路径中删除。

代码实现：

class Solution {
public:
    vector<vector<int>> allPathsSourceTarget(vector<vector<int>>& graph) {
        vector<vector<int>> result;
        vector<int> path;
        dfs(graph, 0, result, path);
        return result;
    }
private:
    void dfs(vector<vector<int>>& graph, int i, vector<vector<int>>& result, vector<int>& path) {
        path.push_back(i);
        if (i == graph.size() - 1)
        {
            result.push_back(path);
        }
        else
        {
            for (int j : graph[i])
            {
                dfs(graph, j, result, path);
            }
        }
        path.pop_back();
    }
};

上述代码中的 path 记录当前路径中的所有节点，result 记录所有已经找到的路径。

上述代码中没有判断一个节点是否已经访问过。在做图搜索的时候通常需要判断一个节点是否已经访问过，这样可以避免反复访问环中的节点。由于这个题目已经明确图是一个有向无环图，因此没有必要担心重复访问环中的节点。

上述代码和实现回溯法的代码很相像，这是因为回溯法从本质上来说就是深度优先搜索。