一、题目名称

LeetCode 129. 求根节点到叶节点数字之和

二、题目要求

给你一个二叉树的根节点 root ，树中每个节点都存放有一个 0 到 9 之间的数字。
每条从根节点到叶节点的路径都代表一个数字：

例如，从根节点到叶节点的路径 1 -> 2 -> 3 表示数字 123 。
计算从根节点到叶节点生成的所有数字之和。

叶节点是指没有子节点的节点。

三、相应举例

示例 1：

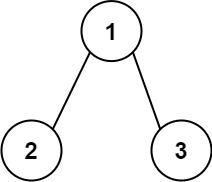
输入：root = [1,2,3]
输出：25
解释：
从根到叶子节点路径 1->2 代表数字 12
从根到叶子节点路径 1->3 代表数字 13
因此，数字总和 = 12 + 13 = 25
示例 2：

输入：root = [4,9,0,5,1]
输出：1026
解释：
从根到叶子节点路径 4->9->5 代表数字 495
从根到叶子节点路径 4->9->1 代表数字 491
从根到叶子节点路径 4->0 代表数字 40
因此，数字总和 = 495 + 491 + 40 = 1026

四、限制要求

树中节点的数目在范围 [1, 1000] 内
0 <= Node.val <= 9
树的深度不超过 10

五、解决办法

深度优先搜索

从根节点开始，遍历每个节点，如果遇到叶子节点，则将叶子节点对应的数字加到数字之和。如果当前节点不是叶子节点，则计算其子节点对应的数字，然后对子节点递归遍历。

计算某一路径之和时，需将当前节点的值乘以10再加子节点对应的值，即10*1+2，可得这条路径上这两个节点之和，以此类推，采用递归方法，即可分别求出左子树和右子树路径之和，然后相加可得总路径之和。

六、代码实现

class Solution {
    public int sumNumbers(TreeNode root) {
        return dfs(root, 0);
    }

    public int dfs(TreeNode root, int prevSum) {
        if (root == null) {
            return 0;
        }
        int sum = prevSum * 10 + root.val;
        if (root.left == null && root.right == null) {
            return sum;
        } else {
            return dfs(root.left, sum) + dfs(root.right, sum);
        }
    }
}