本专栏主要记录力扣的刷题记录,备战蓝桥杯,供复盘和优化算法使用,也希望给大家带来帮助,博主是算法小白,希望各位大佬不要见笑,今天要分享的是——《459.重复的字符串、461. 汉明距离、476. 数字的补数》。
459.重复的字符串
题目描述
给定一个非空的字符串 s ,检查是否可以通过由它的一个子串重复多次构成。
示例 1:
输入: s = "abab" 输出: true 解释: 可由子串 "ab" 重复两次构成。
示例 2:
输入: s = "aba" 输出: false
示例 3:
输入: s = "abcabcabcabc" 输出: true 解释: 可由子串 "abc" 重复四次构成。 (或子串 "abcabc" 重复两次构成。)
解题思路
首先判断字符串长度是不是1,是的话直接返回False,否则用set获取字符串中的单一元素,在s中去数,如果数出来的结果一样,那么说明可以由重复的字符串构成。
解题过程
def repeatedSubstringPattern(s):
if len(s) == 1:
return False
s_set = list(set(s))
target_list = []
for i in s_set:
target_list.append(s.count(i))
if len(set(target_list)) == 1:
return True
else:
return False
忽略了字符串的位置,虽然ab的数量一样,但是位置不一样也不能重复构成字符串。可以尝试用列表元素第一次出现的位置与第二次出现的位置进行切割列表。
def repeatedSubstringPattern(s):
if len(s) == 1:
return False
elif len(set(s)) == 1:
return True
s_set = list(set(s))
for i in range(0,len(s_set)):
list_a = ['a', 'b', 'c', 'a']
first_index = s.index(s_set[i])
try:
sed_indx = s.index(s_set[i], first_index + 1)
except ValueError:
return False
else:
step = sed_indx - first_index #0改成i
print("第二次出现的索引",sed_indx)
print("第一次出现的索引",first_index)
print("步长",step)
begin = s.find(s_set[i])
# print("begin",begin)
while begin+step <= len(s)-1:
if s[begin] == s[begin+step]:
begin += step
else:
return False
return True
忽略了组合中间还包括第一个元素的情况,头痛!用列表切割判断吧!
def repeatedSubstringPattern(s):
if len(s) == 1:
return False
elif len(set(s)) == 1:
return True
s_set = list(set(s))
for i in range(2,int(len(s)/2)+1):
target_str = "".join(s[:i])
s_list= [j for j in s.split(target_str) if j != ""]
if s_list == []:
return True
return False
终于通过了!看看其他大佬的解答,直接震惊我!
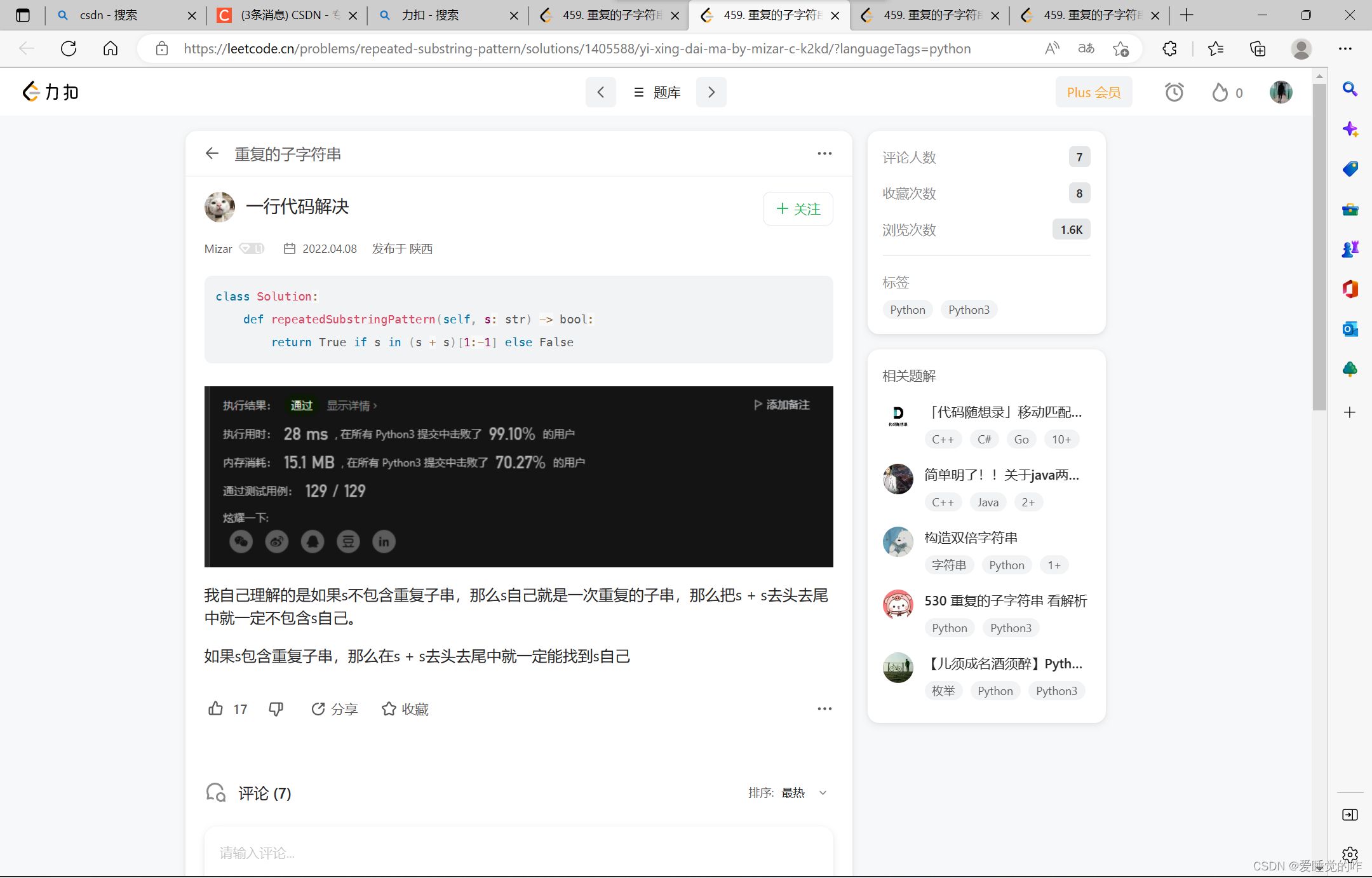
class Solution:
def repeatedSubstringPattern(self, s: str) -> bool:
return True if s in (s + s)[1:-1] else False
如果s不包含重复子串,那么s自己就是一次重复的子串,那么把s + s去头去尾中就一定不包含s自己。
如果s包含重复子串,那么在s + s去头去尾中就一定能找到s自己,这样的做法真的很巧妙!记住了!
461. 汉明距离
题目描述
两个整数之间的 汉明距离 指的是这两个数字对应二进制位不同的位置的数目。
给你两个整数 x 和 y ,计算并返回它们之间的汉明距离。
示例 1:
输入:x = 1, y = 4 输出:2 解释: 1 (0 0 0 1) 4 (0 1 0 0) ↑ ↑ 上面的箭头指出了对应二进制位不同的位置。
示例 2:
输入:x = 3, y = 1 输出:1
解题思路
首先要将传入的整数转化为二进制,可以用bin函数,主要要进行切片,然后将两个二进制数字补齐,短的数字要在前面加0补齐,最后判断各位是否相等,不相等的话count需要进行+1,最后返回count的值。
解题代码
def hammingDistance(x: int, y: int):
x_bin = bin(x)[2:]
y_bin = bin(y)[2:]
max_length = max(len(x_bin),len(y_bin))
min_length = min(len(x_bin),len(y_bin))
if len(x_bin)>len(y_bin):
y_list = [i for i in y_bin]
for i in range(max_length-min_length):
y_list.insert(0,"0")
y_bin = "".join(y_list)
elif len(x_bin)==len(y_bin):
pass
else:
x_list = [i for i in x_bin]
for i in range(max_length-min_length):
x_list.insert(0,"0")
x_bin = "".join(x_list)
count = 0
for i in range(0,len(x_bin)):
if x_bin[i] != y_bin[i]:
count +=1
return count
476. 数字的补数
题目描述
对整数的二进制表示取反(0 变 1 ,1 变 0 )后,再转换为十进制表示,可以得到这个整数的补数。
例如,整数 5 的二进制表示是 "101" ,取反后得到 "010" ,再转回十进制表示得到补数 2 。
给你一个整数 num ,输出它的补数。
示例 1:
输入:num = 5 输出:2 解释:5 的二进制表示为 101(没有前导零位),其补数为 010。所以你需要输出 2 。
示例 2:
输入:num = 1 输出:0 解释:1 的二进制表示为 1(没有前导零位),其补数为 0。所以你需要输出 0 。
解题思路
将整数用bin函数转化为2进制的数,遍历得到的字符串,判断其中的每一个数,得到它的补数,最后用int转化为整数就可以了,返回得到的整数。
解题代码
def findComplement(num: int):
# 转化为2进制
num_bin = bin(num)[2:]
fin_num = ""
for i in num_bin:
if i =="0":
fin_num += "1"
else:
fin_num += "0"
result_num = int(fin_num,2)
return result_num