本题是动态规划的问题,我也在此阐述我对动态规划的理解,如有不准确、缺失、错误,敬请斧正。
题目描述:
给定一个非负整数 numRows,生成「杨辉三角」的前 numRows 行。
在「杨辉三角」中,每个数是它左上方和右上方的数的和。
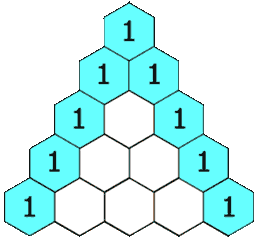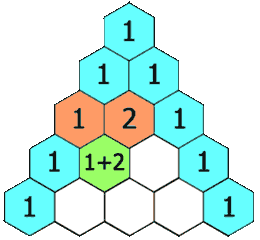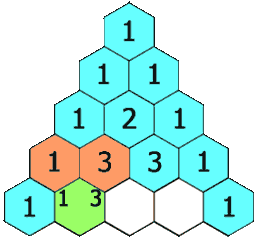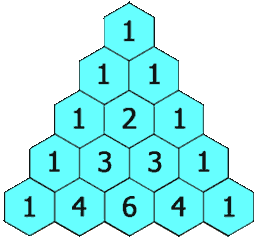
示例 1:
输入: numRows = 5 输出: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]
示例 2:
输入: numRows = 1 输出: [[1]]
提示:
1 <= numRows <= 30
解题准备:
1.了解杨辉三角:杨辉三角不是传统意义上的某种结构,而是一种具有规律的特殊结构,其满足:第一,对于每一行,第一个和最后一个数据都为1===第二,对于每一行,除开第一个和最后一个数据,其它数据等于前一行前一列+前一行同列。【边界值除外,比如第一行】(如果把它看成一个L型的直角三角形则更好理解)
2.理顺题目要求:生成numRows的杨辉三角。所以首要目的是了解杨辉三角。
解题难点1分析:
难点1:存储问题
其实很容易知道,杨辉三角的第i行数据,取决于第i-1行数据,我们首要考虑的,是如何存储第i-1行数据。
有人说,这也难?第一行用个List<Integer> list,然后list.add(1),同理第i-1行,list.add(i-1【的结构】)顺手的事。
不过,list存储没有问题,却消除了第i行和第i-1行之间的列关系(行关系也删除了),而且既不知道i-1行,第i行的数据从何而来?如果再深入,不知道i-2行,第i-1行从何而来?
所以得思考:
如何保持第i行和第i-1的行、列关系?
其实杨辉三角完全可以看成一个numRows*numRows的矩阵。
对于第i行,后面numRos-i的数据都为0,前i个数据为真实数据。【这里的i,从1开始,不是计算机里从0开始】
如果用矩阵存储,那么第1行数据,有matrix【1】【1】=1
第2行,matrix【2】【1】=1;matrix【2】【2】=1;
重点是,第3行及之后,matrix【3】【1】=1;matrix【3】【2】=2;matrix【3】【3】=1;===可以发现,matrix【3】【2】恰好等于matrix【2】【1】+matrix【2】【2】,即解题准备的问题。
因此,使用矩阵(也就是二维数据,即可很好地存储第i行和i-1行的行、列关系)
节约空间:
不过,矩阵的存储,明显要浪费掉接近一半的空间。
已知,杨辉三角,对于第i行,其元素个数=第i-1行的个数+1,有此规律,可以创建更为精简的动态增加的数组,毕竟Java的数组允许事先不new。
难点2:理解问题
有人会有疑问:我知道杨辉三角的规律,可是写起来还是非常困惑。
既然第i行和第i-1行有关系,可是事先只知道第一行?(也许有第二行)
因此,杨辉三角理论上可以用递归的方式解答,不过代码比较难写,因为要输入一个含有i个数据的数组,返回i+1个数据的数组,结束条件为:如果i==1,返回【1】。
有是有,但是写起来相当麻烦和抽象。
不过动态规划的思想解决了该问题,动态规划:把大问题分解成小问题,记录这些小问题的解,最终形成整体答案。
既然只知道第一行和第二行,那么第三行算出来后,记录下来(存储在矩阵里),计算第四行时,再使用不就行了?
我们有第一行的解,就能算出第二行,有第i-1行的解,就能算出第i行。
此时,我们已经有了最小问题的解,把过程数据记录下来,就能算出答案。
代码:
class Solution {
public List<List<Integer>> generate(int numRows) {
List<List<Integer>> result = new ArrayList<>();
Integer data[][] = new Integer[numRows][];
data[0]=new Integer[1];
data[0][0]=1; // 第一行,最小问题的解
// 要求生成numRows行杨辉,从1开始是因为第一行已经生成
for(int i=1; i<numRows; i++){
data[i]=new Integer[i+1];
data[i][0]=1; // 前后一定是1
data[i][i]=1;
// 从1开始,因为0已经赋值,到达i-1,因为i也被赋值
for(int j=1; j<i; j++){
data[i][j]=data[i-1][j-1]+data[i-1][j];
}
}
// asList表示把数组转变为list
for(Integer[] rows:data){
result.add(Arrays.asList(rows));
}
return result;
}
}动态规划的补充:
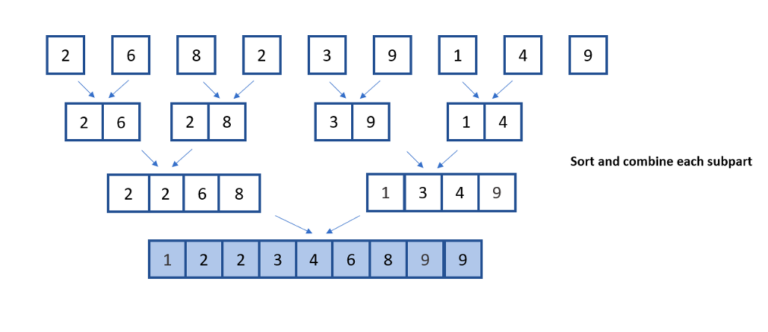
动态规划和分治法有相同之处,都是分解子问题,只是分治法覆盖全面且相互独立,动态规划覆盖全面但有重叠。
动态规划的核心,是拿到状态转移方程,状态转移方程是指,如何从一个子问题,得到问题的解,是一个递归式子。
比如本题,本题想构造numRows行杨辉三角,其难点不是将数据存入list,而是知道如何构造,需要哪些数据(比如i行与i-1行的关系)
如何构造,已知每一行,第1个和最后一个都是1,那么难点就在于中间的数据。中间数据的求解,就涉及状态转移方程。
本题的状态转移方程,就是data【i】【j】=data【i-1】【j-1】+data【i-1】【j】
以上内容即我想分享的关于力扣热题13的一些知识。
我是蚊子码农,如有补充,欢迎在评论区留言。个人也是初学者,知识体系可能没有那么完善,希望各位多多指正,谢谢大家。