目录
1 ECDSA 是什么?
2 理解基础知识
3 为什么使用 ECDSA?
4 基础数学和二进制
5 哈希
6 ECDSA 方程
7 点加法
8 点乘法
9 陷阱门函数!
⚠️ 原文:Understanding How ECDSA Protects Your Data.
⚠️ 写在前面:本文属于搬运博客,自己留着学习。同时,经过几天的折磨后,我对椭圆曲线已经有点基础了,因此删除了一些我认为无关紧要的原文。
1 ECDSA 是什么?
ECDSA 代表 “椭圆曲线数字签名算法”,它用于对数据(例如文件)进行签名,以便让您验证其真实性,同时不损害其安全性。ECDSA 签名与真实签名之间的区别在于,伪造 ECDSA 签名是不可能的。
您不应该将 ECDSA 与 AES(高级加密标准)混淆,后者是用来加密数据的。ECDSA不加密或阻止他人查看或访问您的数据,但它保护的是确保数据未被篡改。
😽 加密是用来加密数据以防泄漏的,签名是用来验证数据是否被篡改的。在第 3 节会再次进行说明。
ECDSA 这一短语中的两个词值得注意,那就是 “曲线” 和 “算法”,因此 ECDSA 本质上都是关于数学的。这些数学知识相当复杂,所以尽管我会尝试使其易于理解,您可能仍然需要一些数学知识才能真正理解它。
2 理解基础知识
原理很简单,假设你有一个数学方程,并在图上画出它的曲线,然后你在曲线上选择一个随机点作为起点。接着你生成一个 随机数,这就是你的 私钥,你用这个 随机数和 “起点” 进行一些神秘的数学运算,你在曲线上得到第二个点,那就是你的 公钥。
可以看出,公钥是由私钥决定的。
当你想要签名一个文件时,你会使用这个私钥和文件的哈希(表示文件的独特数字)进行一个神秘的方程,这将为你生成签名。签名本身分为两部分,称为 R 和 S 。
为了验证签名是否正确,你只需要公钥和签名的一部分(S),将其放入另一个神秘的方程中。如果这个数学方程给了你 R,那么签名是有效的。
我们没有办法知道别人的私钥,也没有办法使用公钥创建签名。
3 为什么使用 ECDSA?
ECDSA 的应用:假设有一个 APP 不希望其数据被用户篡改或修改,比如一个只允许你加载官方地图的游戏,或者一个只允许你安装官方应用程序的手机。
在这些情况下,文件(游戏地图、数据)将使用 ECDSA 签名进行签名,公钥将与 APP /设备捆绑在一起,通过验证签名来确保数据没有被修改,而私钥则被锁在某个安全的地方。
由于你可以使用公钥验证签名,但无法使用它创建/伪造新签名,因此可以将公钥与 APP /设备一起分发而无需担心。这与 AES 加密系统形成对比,后者允许你加密数据,但你需要密钥来解密,这样的 APP 需要捆绑密钥,这就失去了目的。
4 基础数学和二进制
ECDSA 只使用 整数,不使用浮点数。
此外,数字的范围受签名中使用的 位数 的限制。正如你所知,计算机使用 “位” 来表示数据。每次你增加一位,可以表示的最大数字就会翻倍。通常 ECDSA 会使用 160 位总数,所以它能一个非常大的数字,有 49 位数字。
位数越多,可以表示的数字就越大,这意味着更高的安全性,因为很难 “猜测” 到方程中使用的关键数字。
另一个你需要知道的数学结构是 模数,它可以简单地被描述为整数除法的结果。例如,x mod 10 意味着 x 除以 10 的余数。
5 哈希
哈希是一个你应用于数据每个字节的数学方程,它会给你一个独特于你数据的数字。例如,所有字节值的总和可能被认为是一个非常简单的哈希函数。所以如果文件(消息)中的任何东西发生变化,哈希也会完全不同。
在 SHA1 哈希算法 的情况下,结果总是 20 字节(160 位)。它非常有用,可以验证文件是否被修改或损坏,你为任何大小的文件获得 20 字节的哈希,你可以轻松地重新计算这个哈希以确保它匹配。ECDSA 签名的是实际的哈希,所以如果数据发生变化,哈希发生变化,签名就不再有效。
签名是由私钥和文件的哈希值生成的,因此可以说签名是在对文件的哈希值进行签名。
假设有一个简单的哈希函数,它计算对所有数据求和并在结果上使用模数 10 。
文本文件是一系列字节,把文件中的每个字节加起来,然后对结果进行10的模运算,我们最终会得到一个 0 到 9 之间的数字作为最终的哈希值。对于相同的数据,我们总是得到相同的哈希,如果你改变了文件中的一个字节,结果可能就不同了。
改变文件内容后,得到相同哈希的机会是十之一。
事实上,SHA1 算法比我们简单的 “模数10” 哈希函数复杂得多,它会给出一个非常大的数字并且有一个特点,即如果文件中的单个数据位被修改,它会大大改变。
SHA1 算法的结果有 160 位,即是一个有 49 位数字的十进制数。
这使得 SHA1 成为一个非常难以预测、非常安全的哈希算法,发生 “碰撞”(即两个不同文件具有相同的哈希值)的几率非常低,几乎不可能通过伪造数据来得到特定的哈希值。
6 ECDSA 方程
ECDSA 是如何工作的呢?椭圆曲线密码学基于如下形式的方程:
首先你注意到的是有一个模运算。模运算是一个素数(p),它确保所有的值都在 160 位范围内,并允许使用 “模平方根” 和 “模乘法逆元” 数学,这使得计算变得更加容易。
暂时还没学 “模平方根” 和 “模乘法逆元”,应该就是实现小数、负数模运算的方法 😇
由于我们的模数是 p,这意味着上述 y^2 的可能值仅在 0 到 p-1 之间,即我们一共只有 p 个可能值。此外,由于 ECDSA 只处理整数,并且只有一些数字是 “完全平方数”,即是两个整数的平方值,因此假设曲线上满足条件的点有 N 个,那么有 N < p,其中 N 是 0 到 p-1 之间完全平方数的数量。
由于 ECDSA 只处理整数,因此要求 y^2 开方后的结果必须是整数,不能带根号。又因为 y^2 开方后会得到两个结果,即一正一负且绝对值相等的数,因此原文说是 “两个” 整数。针对 “满足条件的点”,假设其坐标为 (x, y),那么 y^2 应该是一个完全平方数且其值落在 0 到 p-1 之间。
由于椭圆曲线是关于 x 轴对称的,即每个 x 对应有两个 y,因此有 N/2 个可能的 x 坐标是有效的。由上述分析可知,ECDSA 中的椭圆曲线上只有有限数量的点,这都是因为 “整数计算” 和 “模数”。
总结一下:ECDSA 方程给了我们一条包含有限个(N 个)有效点的曲线。这是因为 y 的取值受到模数(p)的限制,即 y^2 需要是一个完全平方数。又因为该曲线关于 x 轴对称,所以总共有 N/2 个可能的、有效的 x 坐标。别忘了 N < p!
7 点加法
别问我为什么要这样定义!
“点加法” 被定义为:将一个点 P 加到另一个点 Q 上,将得到一个点 S 。
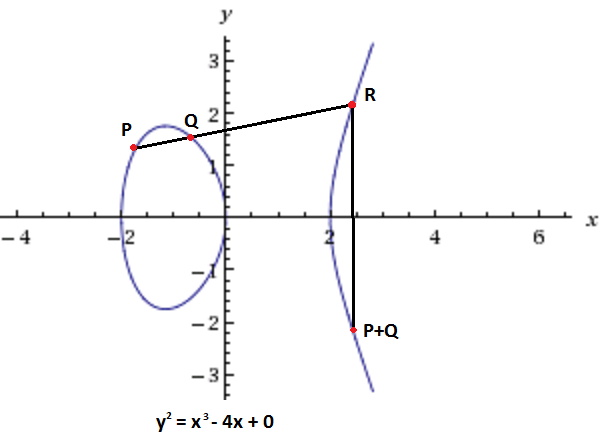
当你从 P 画一条线到 Q 时,它会与曲线在第三个点 R 相交,S 是 R 的负值。
S 点就是图中 P+Q 那个点,只是没有标出来。如果你做 P+P,那么 R 点将是通过点 P 的切线与曲线相交的点。
8 点乘法
P+P+P 可以写成 (P+P)+P,即 P+P+P 是 P+P 的结果点与点 P 的加法,如下图所示。这就定义了 “点乘法”,其中 k*P 是将点 P 加到它自己的 k-1 次和上。

在上图中,你从 P 点作切线,它与曲线相交于第三个点,其对称点是 2P 点。然后,你从 2P 点画线到 P 点,它会与曲线相交于第三个点,其对称点是 3P 点。以此类推,你可以继续进行点乘法。
这就解释了为什么我们每次都要取对称点。因为如果每次都直接取交点,即所谓的 “第三个点”,那么你会发现不管怎么加来加去,得到的点始终在同一条直线上反复横跳,甚至始终都是那两个点(即 P 和 2P 的位置)。
9 陷阱门函数!
“点乘法” 的一个特点是:假设你有一个点 R=k*P,并且你知道 R 和 P 的值,你将无法找出 k 的值。这是由于没有 “点减法” 或 “点除法”,因此你不能轻松地解出 k=R/P 。
或者说,你进行数百万次 “点加法” 后到达曲线上的一个点,但反过来你是很难知道是 “如何” 到达那里的。你不能反转这个操作,也不能找到与点 P 相乘得到结果点 R 的 k 值。
这种即使知道原始点和目标点也无法找到乘数的特性,是 ECDSA 算法安全性的整个基础,这个原则被称为 “陷阱门函数”。
陷阱门函数的进一步介绍可以参考:密码学 | 椭圆曲线 ECC 密码学入门(一)