一、向量化技术在进行神经网络计算时的优势
向量化是一种优化技术,通过使用数组操作代替for循环,可以大大提高代码的性能和效率。在深度学习中尤其明显,可以提高计算效率、简化代码、优化内存使用。
二、如何确保计算时维度是正确的?
(1)先回顾一下神经网络的计算
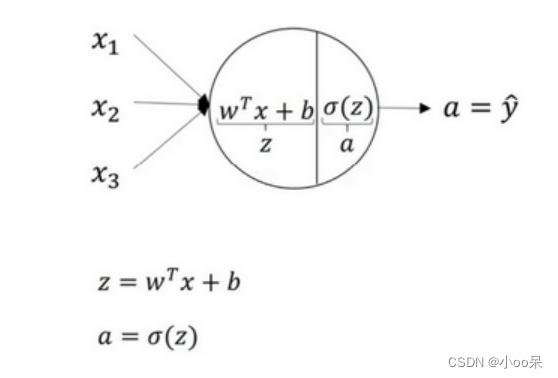
用简单的逻辑回归来举例,用圆圈表示神经网络的计算单元,逻辑回归的计算有两个步骤:
- 首先你按步骤计算出
- 然后通过激活函数g计算出a
一个神经网络只是这样子重复做了好多次计算。
以一个两层的神经网络为例:
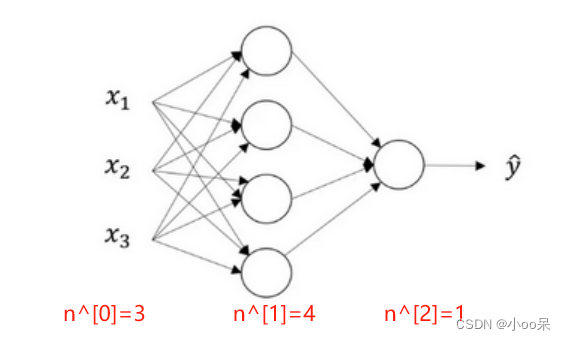
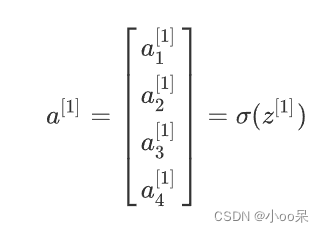
它的第一层计算公式如下:

(2)权重矩阵的维度
对于权重矩阵的维度而言:
- 行维度是神经网络第
层节点的个数
;
- 列维度是前一层
节点的个数
;
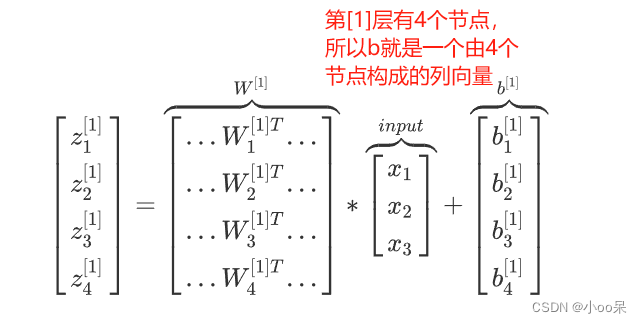
举例说明:对于第一层权重矩阵来说,它的前一层是输出层,所以输出层节点的个数是特征的数量。如下图

(3)输入矩阵的维度
如果输入的是一个样本,那么还不能叫做输入矩阵,还只是输入列向量
如果输入的是训练集(个样本),此时就能称为输入矩阵。

对于输入矩阵也写作
而言:
- 行维度是特征的数量;
- 列维度是样本的数量;
(4)各层输出矩阵的维度
如果只有一个样本,那么各层的输出也只是一个列向量
如果有个样本参与训练,那么此时就能成为输出矩阵
- 行的维度是第
层节点的个数
;
- 列的维度是训练样本的个数
;
(5)偏置列向量的维度
偏置是一个列向量,它在参与计算的时候会通过python的广播机制,变成一个矩阵。
对于第层偏置列向量
而言,它的维度是