排序1：深入了解数据结构第四弹——排序（1）——插入排序和希尔排序-CSDN博客

排序2：深入理解数据结构第五弹——排序（2）——快速排序-CSDN博客

前言：

在前面，我们已经学习了插入排序、堆排序、快速排序等一系列排序，今天我们来讲解一下另一个很高效的排序方法——归并排序

目录

一、归并排序的思想

二、归并排序的递归实现

---

一、归并排序的思想

归并排序是一种经典的排序算法，它采用了分治法的思想。分治法的核心是“分而治之”，即将一个复杂的问题分解成两个或多个相同或相似的子问题，将这些子问题逐个解决，最后将子问题的解合并以解决原问题。

归并排序的基本思想如下：

1. 分解（Divide）：

   • 将待排序的数组从中间分成两半，递归地对这两半分别进行归并排序。
   • 一直分解，直到每个子数组只包含一个元素，因为一个元素的数组自然是有序的。

2. 解决（Conquer）：

   • 当分解到最小子问题时，即每个子数组只有一个元素时，开始解决这些小问题。
   • 解决的方式是合并（Merge）两个有序的子数组，从而得到一个更大的有序数组。

3. 合并（Merge）：

   • 合并过程是归并排序的关键步骤。它将两个有序的子数组合并成一个有序的数组。
   • 通常使用两个指针分别指向两个子数组的起始位置，然后比较两个指针所指向的元素，将较小的元素放入结果数组中，并移动该指针。
   • 重复这个过程，直到一个子数组被完全合并到结果数组中，然后将另一个子数组的剩余元素直接复制到结果数组中。

归并排序的操作如下：

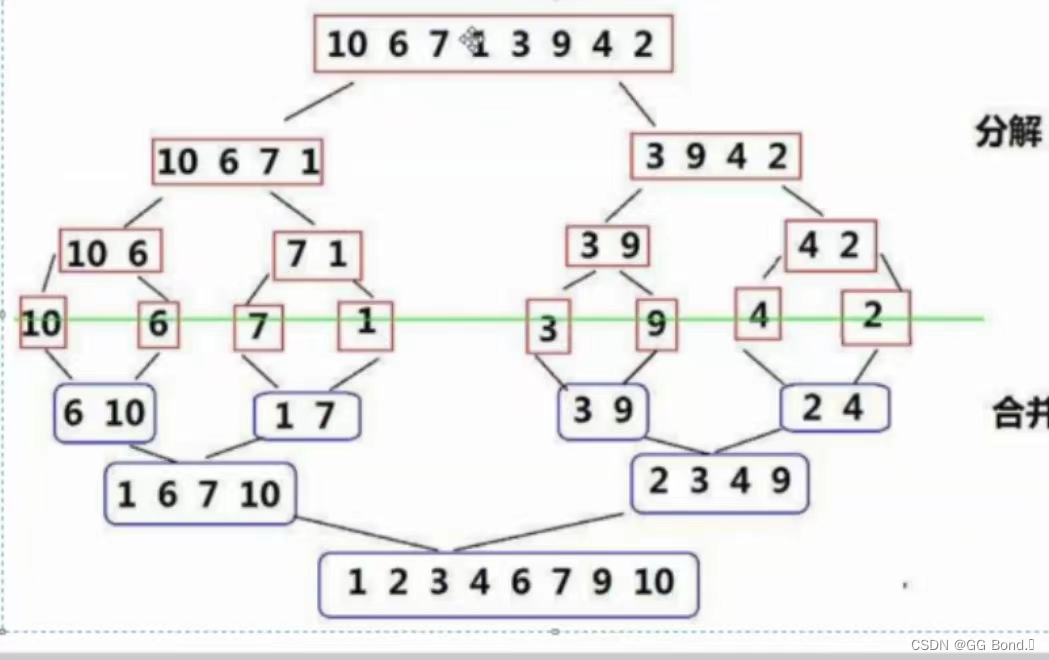
归并操作其实就是将一组数据通过递归等不断划分成两个部分，直到划分到一个元素之后，再对这两部分排序排进一个数组内，相当于把划分的过程再反过来走了一遍，只是走回去的过程中会把数组一步一步的有序化

二、归并排序的递归实现

递归的实现其实是很有意思的，在上面我们已经讲了递归的思想，其实就是不断的重复划分然后排序的过程，所以我们就可以设计一个递归来实现这种，同时，由于每一步都要进行分区划分，所以我们可以封装一个划分函数（_MergeSort函数）在前，重复这个过程

void MergeSort(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);

	_MergeSort(a, 0, n - 1,tmp);

	free(tmp);
}

1、因为我们在划分结束后，需要将各个小的部分再排序成一个有序的大部分，所以我们创建一个tmp的指针指向一个与原数组一样大小的空间，然后每一次排序放进这个空间，最后再把这个空间中的数据复制回原数组

2、其中_MergeSort函数内参数分别为原数组指针，首元素位置，尾元素位置，tmp指针

//归并排序
void _MergeSort(int* a, int begin,int end,int* tmp)
{
	if (begin == end)
		return;

	//小区间优化
	if (end - begin + 1 < 10)
	{
		InsertSort(a + begin, begin - end + 1);
	}

	int mid = (begin + end) / 2;
	_MergeSort(a, begin, mid, tmp);
	_MergeSort(a, mid + 1, end, tmp);
	
	int begin1 = begin, end1 = mid;
	int begin2 = mid + 1, end2 = end;
	int i = begin;
	while (begin1 <= end1 && begin2 <= end2)
	{
		if (a[begin1] < a[begin2])
		{
			tmp[i++] = a[begin1];
			begin1++;
		}
		else
			tmp[i++] = a[begin2++];
	}
	while (begin1 <= end1)
	{
		tmp[i++] = a[begin1++];
	}
	while (begin2 <= end2)
	{
		tmp[i++] = a[begin2++];
	}
	memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1));
}