1.直接插入排序
直接插入排序是一种简单的插入排序,它的基本思想是:
把待排序的数据按其关键码值的大小逐个插入到一个已经排好序的有序序列中,直到所有的数据都插入完位置,就得到了一个新的有序序列。
我们可以看到他的前提是要有一个有序序列,然后插入一个数据到这个有序序列中使其仍然有序,怎么去找一个有序序列呢?我们可以认为,只有一个数据的时候他就是有序的。就比如下面的一个数组:

他用直接排序的思路是怎么排的呢?
首先我们要将第一个数据 8 看成一个有序序列,这时 [0 ,0] 这个区间就是有序的,这时候我们在将第二个数据 5 插入到有序序列中,我们要保证 [0,1] 还是一个有序序列,我们先假设新插入的数据就在最后,这时候他要和前面的数据进行大小比较,5<8 ,所以 5 和 8 要调换位置,这时候5 就到了有序序列的头部,前面已经没有要比较的数据了,这时候 5 就插入完成了 。而新序列 [0 ,1] 这个区间 又是一个新的有序序列。
 这时候再插入 [0,1] 后面的 0 插入到有序序列中, 0首先与8比较,然后0和8调换位置,然后0再与5相比较,0再与5调换位置
这时候再插入 [0,1] 后面的 0 插入到有序序列中, 0首先与8比较,然后0和8调换位置,然后0再与5相比较,0再与5调换位置

这时候 [0,2]这个区间又是一个有序序列了,这时候我们就能写出直接插入排序的单趟排序的代码了。 首先数组中有一个有序区间是 [0 ,end] , 然后再把 a [end+1]插入到有序序列中。
//[0,end]有序,将a[end+1]插入
while (end>=0 && a[end+1] < a[end])
{
Swap(&a[end], &a[end + 1]);
end--;
}单趟排序整完了,我们就只要控制 end 就完成整个排序了,而有序序列最开始就只有一个数据,也就是[0,0]这个区间,假如数据个数为n的话,最后一趟排序就是最后一个数据插入到 [0,n-2] 这个有序序列中,所以 end 的最大值就是n-2。再用一层循环来控制end就完成直接插入排序了。
//交换函数
void Swap(int* px, int* py)
{
int tmp = *px;
*px = *py;
*py = tmp;
}
//直接插入排序
void _Insert(int* a,int n)
{
assert(a);
int i = 0;
for (i = 0; i <= n - 2; i++)
{
int end = i;
//[0,end]有序,将a[end+1]插入
while (end >= 0 && a[end + 1] < a[end])
{
Swap(&a[end], &a[end + 1]);
end--;
}
}
}
直接插入排序有什么特点呢?
首先就是直接插入排序对于本来就有序或者接近有序的数据会很有优势,这时候就相当于遍历了一遍数组,基本没有交换,效率很高。
但是直接插入排序对于逆序的数据会很吃力,以为每次插入一个新数据,都要从最后的位置逐个替换到数组首位,时间复杂度为O(N^2)
2.希尔排序
希尔排序是对直接插入排序的一种优化。因为直接插入排序对于逆序的数据排序的时间复杂度很高,所以希尔排序的逻辑是先进行预排序,是数据接近有序,然后再进行直接排序。
希尔排序的第一个步骤就是预排序,把间隔为 gap 的数据分为一组,进行插入排序。

那上面的数组来举例,假设 gap=3 时,把数组中间隔为gap的数据分为一组,然后对他们进行直接插入排序。比如上面的 0 ,1 ,4 ,10是一组,首先 0 看成一个有序序列,把1插入进去,然后再把 4 插入进去 ,最后再把10 插入进去。预排序的逻辑就是这样,跟直接插入排序差不多,直接插入排序的gap相对于1,这里只是将间隔为gap的数据看成一组。
这时候要怎么来控制 end 呢,[0,end]有序,end的最小值就是0,把a[end+gap]插入到有序序列中,那么我们的 end 的最大值就是n-1-gap,每次交换完之后end更新为前一个数据的位置end-gap,那么单趟排序的实现就是下面这样的:
while (end>=0&&a[end + gap] < a[end])
{
Swap(&a[end], &a[end + gap]);
end -= gap;
}
我们可测试一下上面的数据当gap为3时单趟排序的结果对不对。
我们画图可以得出的结果是:

每一组间隔为gap的数据都是有序的
//希尔排序
void ShellSort(int* a, int n)
{
assert(a);
int gap = 3;
int i = 0;
for (i = 0; i <= n - 1 - gap; i++)
{
int end = i;
//[0,end]有序,插入a[end+gap]
while (end >= 0 && a[end + gap] < a[end])
{
Swap(&a[end], &a[end + gap]);
end -= gap;
}
}
}

单趟排序搞定之后剩下的就很简单了,希尔排序除了预排序的思想,其次的就是 gap 的控制了,为什么要有 gap 为间隔来预排序? 试想,当原数组的数据是接近逆序的时候,他的大的数据在前面,而小的数据在后面,如果采用直接排序的话就需要一个位置一个位置交换,十分的耗时,当我们用预排序的话,他不是一次只移动一个位置,而是一次移动gap个位置,这样一来能让小的数据更快地来到数组的前面,大的数据也能更快的调换到后面,使得原本逆序的数组变得更接近有序,更有利于插入排序。同时,希尔排序一般是用于排序数据量很大的时候,这时候也能让更大的数据更快的到后面,小的数据更快的到前面,这样优化了直接插入排序。
但是gap该如何确定呢?当数据量大的时候gap相应地就要大,而当数据量小的时候gap相应地就要小,所以gap是与数据个数n有关的。前面我们说过当gap为 1 的时候,希尔排序就是直接插入排序。
思考一个问题,希尔排序只能进行一次预排序吗? 我们可以用多次预排序来使得原数组接近有序,但是每一次的gap都要改变,而最后一趟预排序的 gap 一定要为 1 ,确保最后一趟是直接插入排序。我们可以用数据量 N / 2 来初始化第一趟预排序的gap,然后每一趟预排序的gap都是上一趟的 gap/2 ,这样就能确保最后一趟的gap为1,也可以用 N/3+1来表示第一趟预排序gap,每次的gap是上一次的gap/3+1,这样也能确保gap最后一次为1。多次排序的目的就是为了使得数据更接近有序,两趟相邻预排序的gap不能太过接近,这样的话预排序次数过多,时间复杂度过高,而两趟相邻预排序的gap也不能差距过大,差距太大的话预排序的程度不够,无法使数据接近有序,到最后gap为1时的时间消耗大。 上面我们举例的两种就是目前程序员常用的两种gap的值的定义。
这样一来,我们只要控制好gap就能完成希尔排序了,我们知道最后一趟直接排序的gap为1,如何控制循环跳出条件呢?我们可以在循环内部预排序完了之后用一个判断和break来跳出循环if(gap==1) braek,也可以在循环条件中判断 gap>1 进入循环,然后再预排序之间修改gap,这种情况要把gap初始化为n。
//希尔排序
void ShellSort(int* a, int n)
{
assert(a);
int gap =n;
while (gap > 1)
{
gap= gap / 3 + 1;
int i = 0;
for (i = 0; i <= n - 1 - gap; i++)
{
int end = i;
//[0,end]有序,插入a[end+gap]
while (end >= 0 && a[end + gap] < a[end])
{
Swap(&a[end], &a[end + gap]);
end -= gap;
}
}
}
}
我们可以来测试一下直接插入排序和希尔排序的效率,看一下希尔排序是否比直接插入排序快。
void test()
{
int a[] = { 0, 5, 8, 1, 3, 2, 4, 6, 7, 10, 9 };
int b[] = { 0, 5, 8, 1, 3, 2, 4, 6, 7, 10, 9 };
int n = sizeof(a) / sizeof(a[0]);
int begin1 = clock();
_InsertSort(a, n);
int end1 = clock();
printf("_InsertSort:%d\n",end1-begin1);
int begin2 = clock();
ShellSort(b, n);
int end2 = clock();
printf("ShellSort:%d\n",end2-begin2);
}clock是一个系统时钟,他能返回程序执行到这行代码的时间,单位是毫秒,当我们用 end-begin就能表示出一个算法所耗的时间。
当数据量很小的时候,因为计算机处理速度很快,几乎就是一瞬间就完成了,看不出差距。

当吧两个数组都换成逆序的数组时,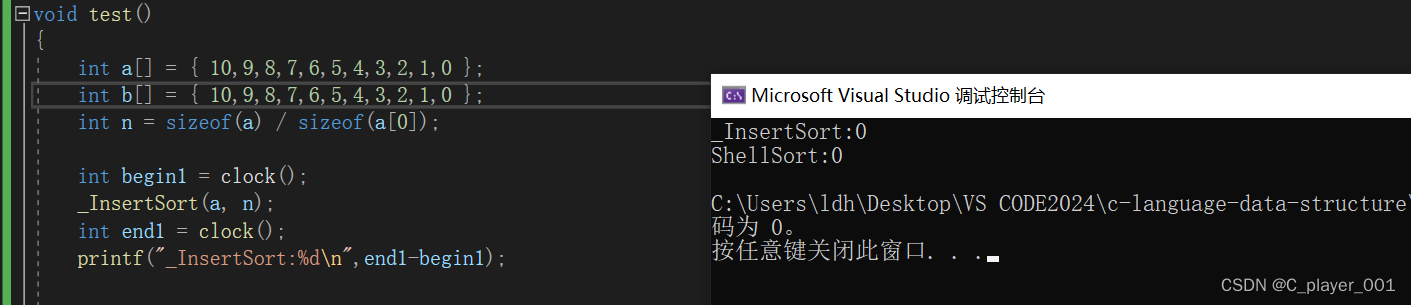
还是看不出差距。
当我们用一万个随机数据排序的时候。
int N = 10000;
int* a1 = (int*)malloc(sizeof(int) * N);
assert(a1);
int* a2 = (int*)malloc(sizeof(int) * N);
assert(a2);
srand((unsigned int)time(NULL));
for (int i = 0; i < N; i++)
{
int data = rand();
a1[i] = data;
a2[i] = data;
}
int begin1 = clock();
_InsertSort(a1, N);
int end1 = clock();
printf("_InsertSort:%d\n",end1-begin1);
int begin2 = clock();
ShellSort(a2, N);
int end2 = clock();
printf("ShellSort:%d\n",end2-begin2);
free(a1);
free(a2);
这时候他们的差距就体现出来了,几乎就不在一个量级了。
如果排序一百万了数据呢?(OS:跑了半天没跑出来),换成十万个数据试一下

十万个数据的时候插入排序的时间就很长了。我们还可以加入之前实现的堆排序来对比一下,堆排序这是之前我们所学习的效率最快的排序算法了。
//向下调整 大堆
void AdjustDown(int* a, int begin, int end)
{
int parent = begin;
while (parent<end)
{
int maxchild = 2 * parent + 1;
if (maxchild > end)
break;
if (maxchild + 1 <= end)
{
if (a[maxchild] < a[maxchild + 1])
{
maxchild += 1;
}
}
if (a[maxchild] > a[parent])
{
Swap(&a[maxchild], &a[parent]);
parent = maxchild;
}
else
{
break;
}
}
}
//删除堆顶元素
void HeapPop(int* a, int size)
{
assert(a);
Swap(&a[0], &a[size - 1]);
size--;
AdjustDown(a,0, size-1);
}
//建堆
void CreatHeap(int* a, int size)
{
assert(a);
int end = (size - 1 - 1) / 2;
while (end>=0)
{
AdjustDown(a, end, size-1);
end--;
}
}
//堆排序
void HeapSort(int* a, int size)
{
assert(a);
CreatHeap(a, size);
while (size)
{
HeapPop(a, size);
size--;
}
}
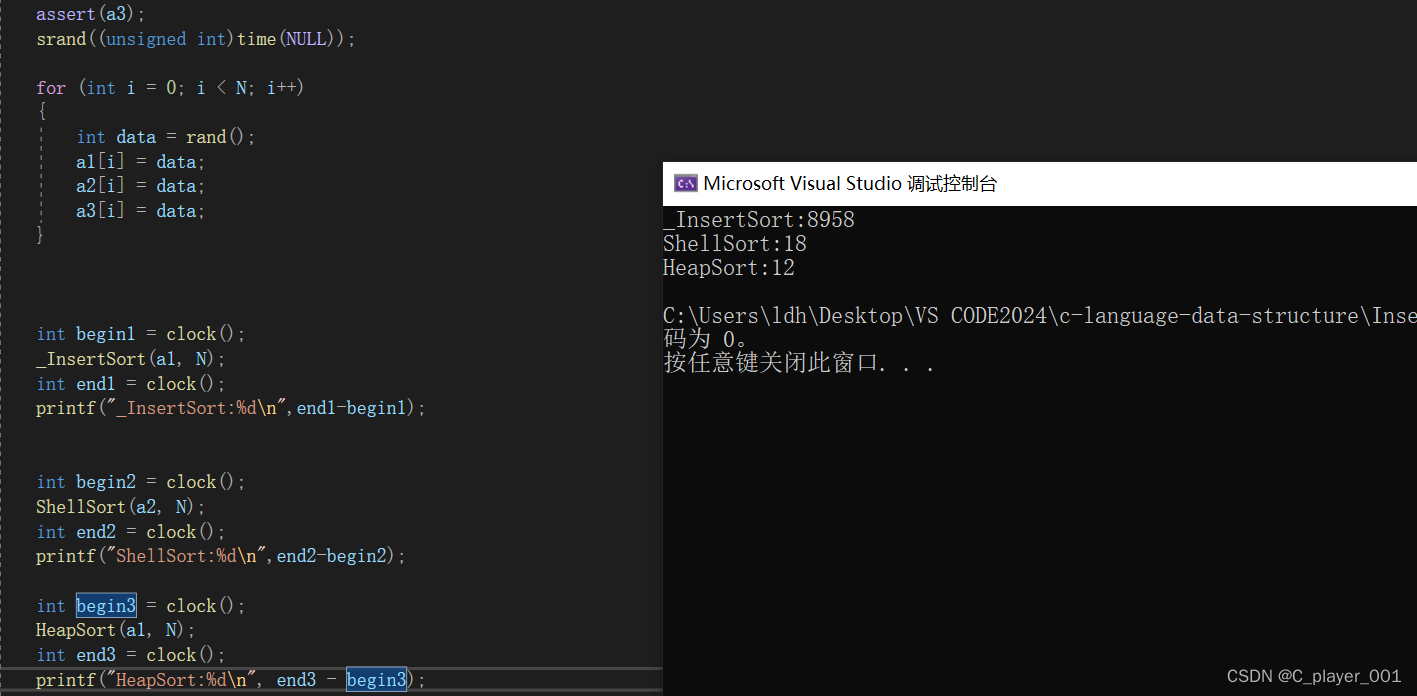
我们可以发现,在数据量为100000时,希尔排序已经几乎和堆排序一个等级了,
然后我们测试一百万个随机数排序时堆排序和希尔排序的效率

数据量为一千万时
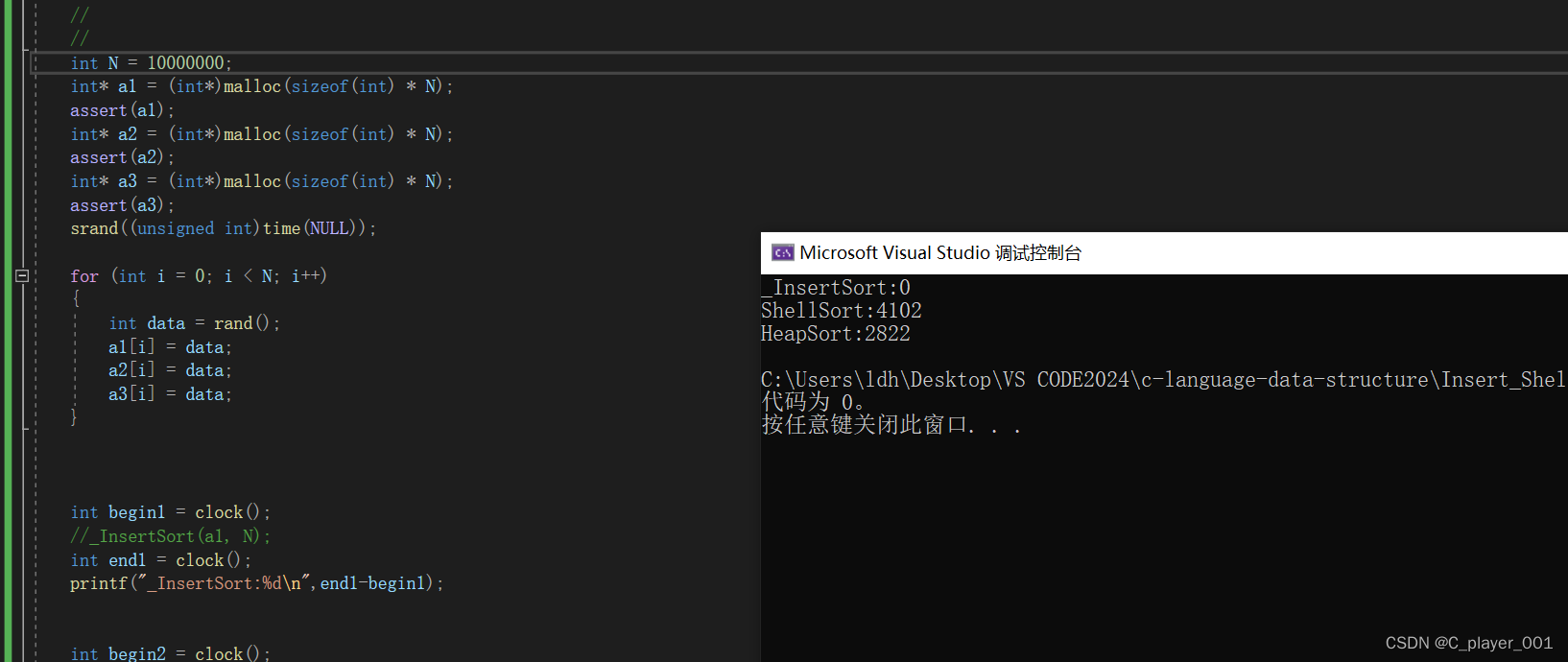
虽然希尔排序还是比不上堆排序,但是相对于直接插入排序他已经提升的十分大了。
希尔排序的时间复杂度是不好算的,因为每一次预排序都会对下一次预排序产生影响,而现在大多数人认可的希尔排序的时间复杂度就是 O(N^1.3),效率略差于NlogN。
这里我们为什么直接创建数组而是要malloc数组呢?因为正常创建的数组是存储在栈区的,而栈区的空间不是很大,只有几兆的大小,而堆区通常有一两个G,所以大数据存在堆区,而栈区有可能存不下。