内容来源：量子前哨（ID：Qforepost）

编辑丨浪味仙  排版丨 沛贤

深度好文：3000字丨15分钟阅读

趋利避害，是所有生物遵循的自然法则，人类也不例外。

举个例子，假如你是某生鲜平台的配送员，载着满满一电瓶车货物，要将其配送至片区内多个住户。

在多劳多得的规则下，要想多赚点配送费，你就不得不合理规划配送路径，尽量少走回头路，以最快速度完成配送，最终返回站点。

如果是你，会怎样规划路线？

都说世界是数学的，生活中诸如此类的困扰，都可以归为一类，叫做组合优化问题：在有限个可能解的集合中，找出最优解。

如何顺应人类趋利避害的天性，做出利益最大化的抉择？还得是魔法打败魔法。

现在可以请出今天的主角最大割问题 (Max-Cut Problem)：一种能够帮我们合理规划复杂组合关系的数学问题。

01

何为最大割问题？

对绝大多数不熟悉数学或编程的读者来说，一看「最大割」这仨字，必然断定它是个既枯燥又难懂的学术名词。

事实上，它蛮有趣、也并不难懂。

在解释概念之前，各位不妨先听个故事，名字叫做《该死，美猴王那纷纷扰扰的花果山》。

话说，花果山上有只石猴，獐鹿为友，猕猿为亲，携众猴入驻花果山后，被拥立为美猴王。

可美猴王也有烦恼：正所谓猴性顽劣，目之所及，众猴抢盆夺碗，占灶争床，眼瞅花果山恐再无宁时，真真是头疼。

于是，美猴王体内趋利避害的远古基因开始觉醒：怎样才能让花果山最大程度地保持和平？

不如取消原有大杂居，试试分区管理？可碍于辖区内面积有限，只有两座山头可分，又该怎么分呢？

美猴王开始了一场思想实验。

情况 1：假设有 2 只见面就掐架的猴，外加两座猴山；

这种情况下，总共有 4 种分区方案。

那么，在这 4 种方案中，哪种最能维持整体和平呢？

我们将这 2 只猴看作一组关系，通过辅助线（实线代表小猴之间见面就掐的矛盾）来观察。 

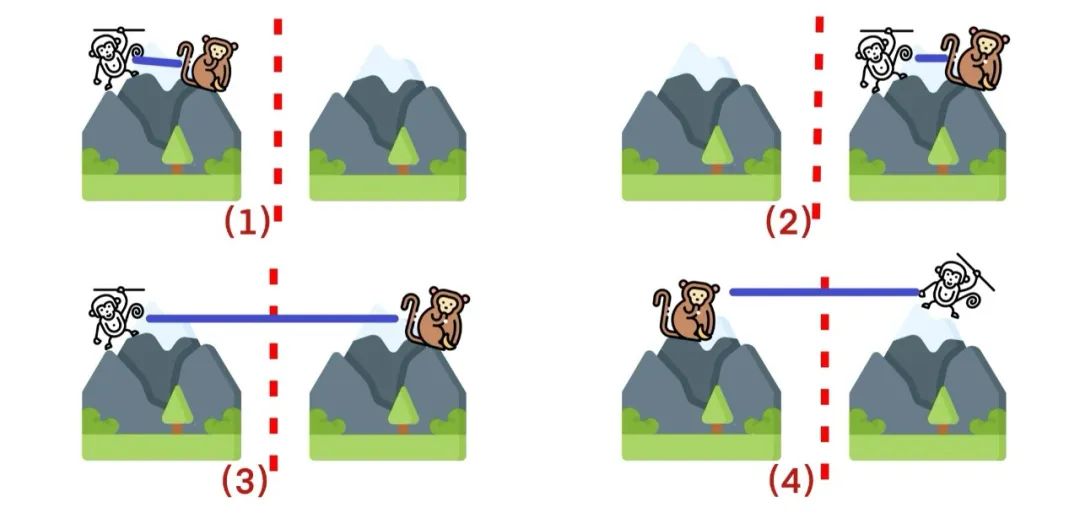
可以看到，切割这组猴的关系线时，图 1 和 2 没有线被切断，图 3 和 4 切断线的数量为 1。

这意味着，此种情况下，切断 1 条关系线的方案，可以维持花果山和平。

情况 2：假设有 4 只彼此都不服的猴，外加两座猴山；

这种情况下，总共有 16 种分区方案。(出于篇幅考虑，下面仅展示 4 种。)

在这些方案中，哪种最能维持花果山和平呢？我们依然将 4 只猴看作一组关系，通过辅助线来观察。

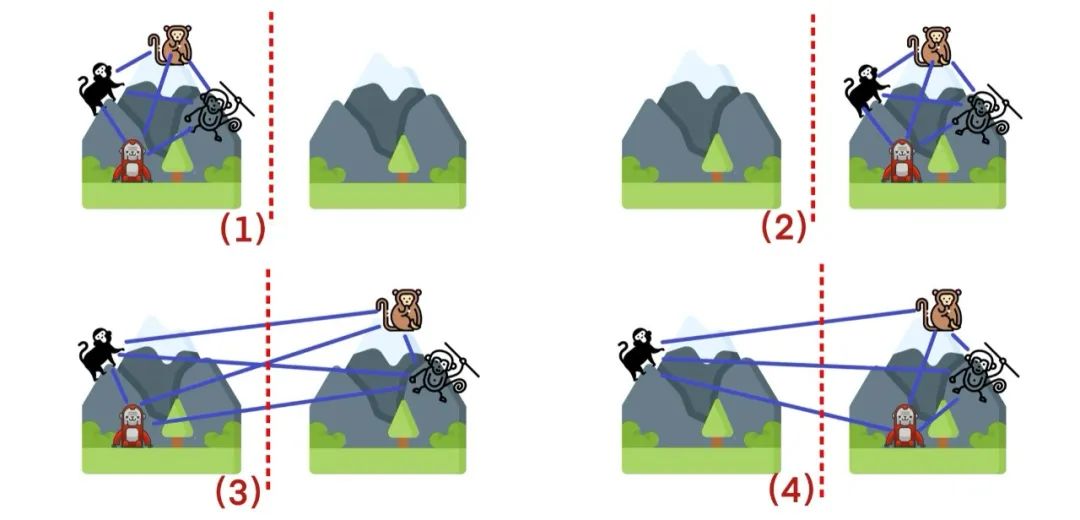
可以看到，在切割这组包含 4 只猴的关系线时，图 3 被切断的线最多，数量为 4。

也就是说，在此种情况下，切断 4 条关系线的方案，最能维持花果山和平。

情况 3：假设有 5 只猴 (有些猴之间有矛盾，有些猴之间没有，仍用连线表示)，外加两座猴山；

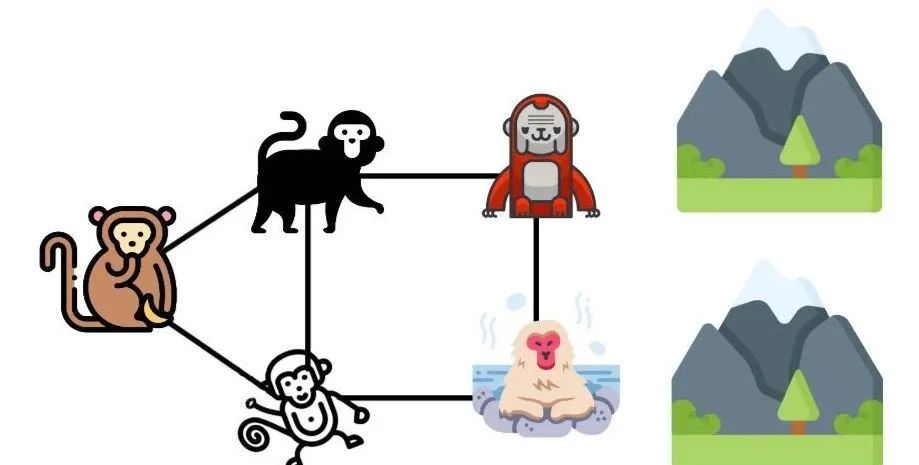
这种情况下，怎样将这 5 只猴合理分开呢？感兴趣的读者可以找张纸画一画。

根据前两种假设我们可知，最能维持花果山和平的方案，被切断的关系线数量一定最多。

放在此种假设中，最优方案切断的数量线为 5 条 (尽管右侧山上其中两只猴也有矛盾，但这种分割法已经是最优解了)。 

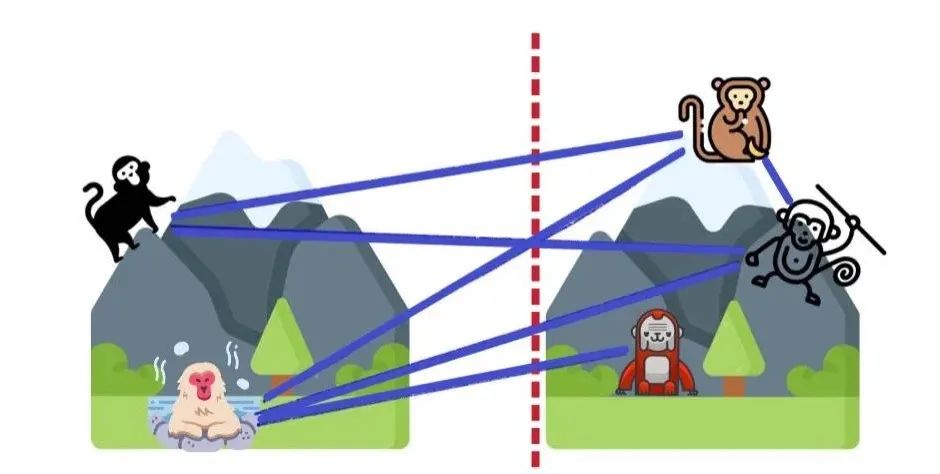
换成平面切割视图，则是这样：

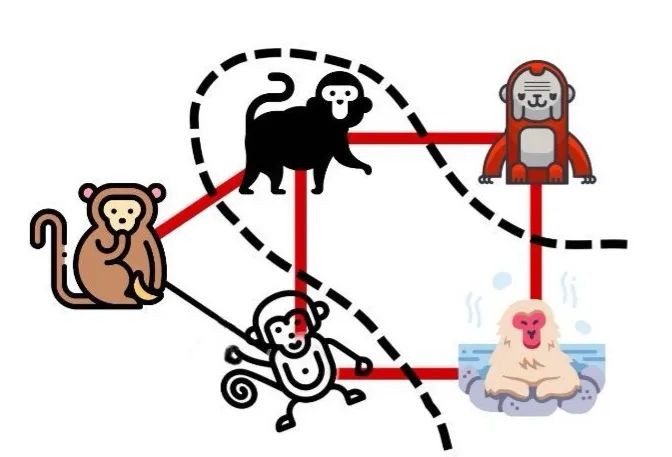
OK，故事听到这里，恭喜，你已经会求解最大割问题了。

所谓最大割 Max-Cut 问题，就是求一种分割方法：给定一张无向图，将所有顶点分割成两群，使得同时被切断的边数量最大。

故事中，猴子对应图中的顶点，俩猴之间的矛盾则对应边。

但你有没有留意到，在前面的假设中，我们默认猴子间的矛盾值都相同，倘若不同呢？比如猴甲与猴乙之间有杀父之仇夺妻之恨，见面肯定以死相拼；但猴甲和猴丁只是因为昨天分桃时猴丁插了个队，见面顶多会呸一声。

实际生活中，在矛盾值有高有低的情况下，我们还需要优先把一言不合便要掐个你死我活的隔开。

当每条边都有一个权重系数时，分割目标函数的思路就会发生变化，从使被切断的边数量最大，变为使切割边的总权重之和最大。这种情况较刚才的假设更为复杂，我们称其为加权最大割问题。

到此，最大割问题的描述就讲完了，这种轻松涨知识的感觉是不是还不赖？诶等等，各位先别急着开香槟。

这个世界，远比想象中复杂。

02

最大割问题为何难解？

刚才是谁按下了各位开香槟的手？哦对，是我，但我是有原因的。

不知各位读者有没有留意到，刚才发生在美猴王故事中的几种假设，我们都能靠手工画图完成。

从专业角度来说，我们用的是穷举法。  

穷举法，是指根据题目给定的约束条件，从可能的集合中一一列举出问题答案，再依次判定：令命题成立者，即为解。

一言以蔽之：大力出奇迹。

倘若不是 2、4、5 只猴子，而是 10、50、100、甚至直接捅穿猴子窝成千上万只猴子，我们还能用穷举法计算出结果吗？

不能。

这里存在一个被称为「计算复杂度」的巨大挑战。

在计算机科学中，一个问题的计算复杂度，就是看运行这个算法所需要的资源量，特别是时间 (CPU 占用时间) 和空间 (内存占用时间)。如果问题的计算复杂度比较高，当问题的变量数增大时，需要筛选的备选答案数量（我们称之为“解空间”）就可能以极快的速度增加。

当需要筛选的可能答案数量过于巨大时，哪怕派出当今运行速度最快的计算机也极难完成，因为计算机需要太多时间来验证所有方案的可能性。

这时，局面就会开始失控。

比如旅行商问题：3 句话就能描述清楚，但很小的变量数就能形成一个极其庞大的解空间，从而使得用计算机去穷举的“蛮力解法”耗时变得极长。 

旅行商问题：一个商品推销员要遍访多个城市，期间所有城市不能重复经过，最后回到出发城市。

他该如何规划最短路径？

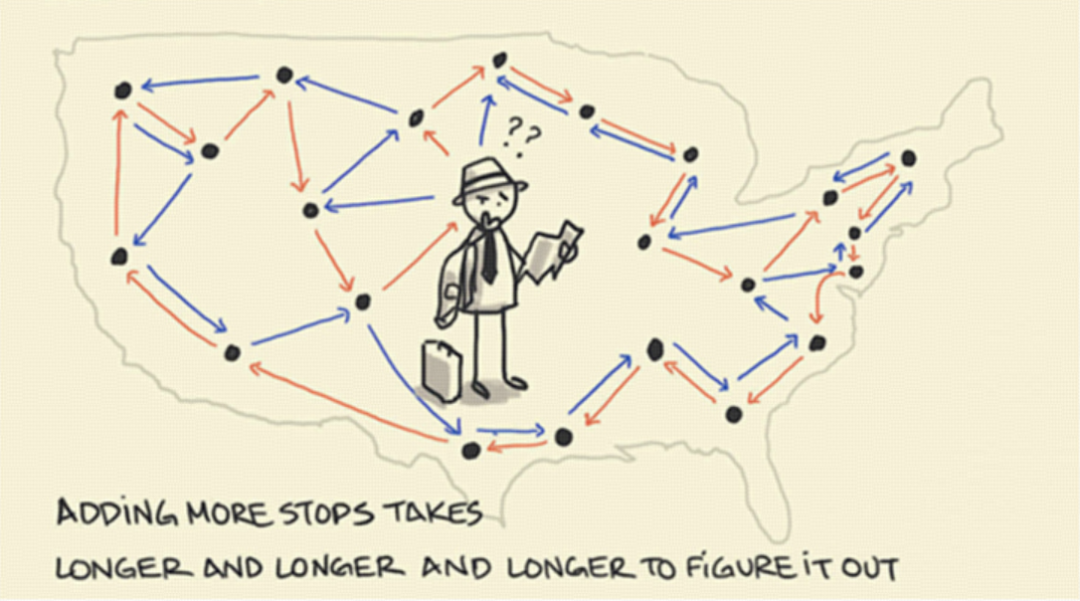
旅行商问题的描述看上去很简单吧？直觉上是不是很好求解？

但是！从数学角度来看，它的挑战在于，随着城市数的增加，求解的计算量会呈“阶乘级”上升。

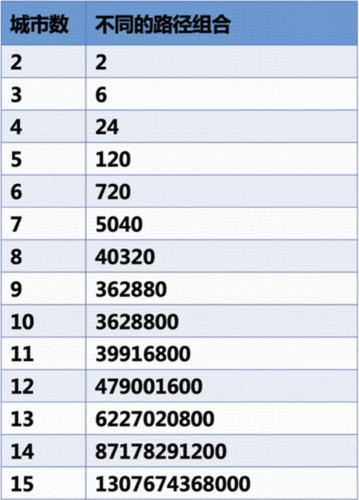
大家能一眼就念出 15 个城市可能存在的路径组合数量吗？

数学上，我们用一个非常形象的词来描述这种现象，叫做「组合爆炸」：变量 (城市数) 只是增加了一点点，解空间的可能性就快速增长成一个极其庞大的规模。

回到花果山的故事中，当猴子数量、矛盾关系数量持续增加时，美猴王所要考虑的分割方案的数量同样会呈阶乘级增长，再也没法用简单的“画图穷举”的方法去求解了。

至此，我们可以对最大割问题做个简单总结：

1) 作为组合优化问题的一种，随着问题规模的增加，可能的解决方案数量会呈阶乘级增长；（采用穷举法，几乎不可能在可接受的时间内找到全局最优解。）

2) 当解决方案数量呈阶乘级增长时，求解组合优化问题的难度，将大大超出经典计算机的能力范围。

03

最大割问题有何现实意义？

你或许会想，尽管明白了什么是最大割问题，但它有什么用呢？现实生活中哪儿有那么多调皮的小猴需要我去调度？

诶，千万别小瞧了它。

德国当代著名作家丹尼尔·凯曼说过：“数学并不会使人脱离现实世界，恰恰相反，数学牵引着现实，让人更加接近现实，让现实更加清晰。”

最大割问题，就是这句话的优雅诠释。

远的不提，咱就拿自动驾驶来说，汽车要想安全地自行驾驶，必须得能感知周围环境，除了要能“认清”车辆行人的行动轨迹，还得能分清路面移动的物体是野猫还是塑料袋，从而精准避障。

但汽车的“眼睛”是摄像头和雷达，这些感官设备带给它的只是一堆一堆的 01 数据，还需要它的大脑去“识别”这些数据所代表的“具体含义”。

以摄像头为例，它所获取的是一帧帧平面二维图片，图片则由一个个不同色值的像素点构成。至于哪些像素点应该被归纳为物体 A，哪些像素点应该被归纳为物体 B，就需要自动驾驶的“大脑”去计算和识别。

要实现这一点，离不开图像分割技术，也就是通过将图像划分成互不相交的区域，实现物体分离，再一一将这些物体识别成不同的对象，进而去判断这些对象会不会动、会怎么动，与汽车自身的运动会不会产生碰撞等，这才能让汽车“看清楚路”。

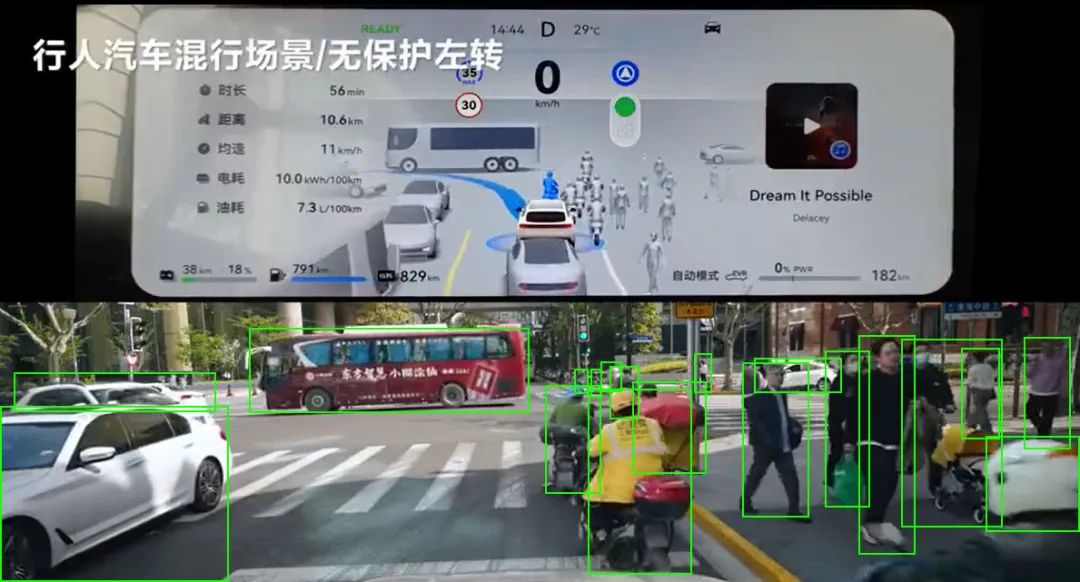
最大割问题可以帮助完成图像分割。

汽车周身摄像头拍摄到的画面，可以将其映射为带权无向图，像素视为图中节点。这样一来，图像分割问题就转化成了图的顶点划分问题，利用最小剪切准则，得到图像的最佳分割，汽车就能“看见”路况，进而科学决策，做到安全驾驶。

而这只是最大割问题应用的冰山一角，事实上，它的应用或变体遍布整个商业领域，是构成我们数字社会非常重要的算法基础。 

1、金融：动态投资组合优化、欺诈检测、信用评估、客户划分；

2、通信：MIMO 波束选择及资源分配；

3、设计：电路板优化设计；

4、能源：主动配电网的路径优化；

5、交通：大规模交通流路径规划；

6、物流：包裹配送优化、物流仓布局；

7、医疗：疾病诊断与医学图像分析；

8、生物制药：小分子对接筛选；

9、工业制造：生产流程优化、整体质量控制流程优化；

10、电子商务：产品推荐、库存管理；

... ...

“世界是数学的。”美国思想家爱默生说：“在它巨大流畅的曲线中没有意外。”

要我说，意外还是有的。

你瞧，在如何发现世界中的数学、如何用好数学等方面，都藏着意外。