目录
力扣1926. 迷宫中离入口最近的出口
解析代码
力扣1926. 迷宫中离入口最近的出口
1926. 迷宫中离入口最近的出口
难度 中等
给你一个 m x n 的迷宫矩阵 maze (下标从 0 开始),矩阵中有空格子(用 '.' 表示)和墙(用 '+' 表示)。同时给你迷宫的入口 entrance ,用 entrance = [entrancerow, entrancecol] 表示你一开始所在格子的行和列。
每一步操作,你可以往 上,下,左 或者 右 移动一个格子。你不能进入墙所在的格子,你也不能离开迷宫。你的目标是找到离 entrance 最近 的出口。出口 的含义是 maze 边界 上的 空格子。entrance 格子 不算 出口。
请你返回从 entrance 到最近出口的最短路径的 步数 ,如果不存在这样的路径,请你返回 -1 。
示例 1:

输入:maze = [["+","+",".","+"],[".",".",".","+"],["+","+","+","."]], entrance = [1,2] 输出:1 解释:总共有 3 个出口,分别位于 (1,0),(0,2) 和 (2,3) 。 一开始,你在入口格子 (1,2) 处。 - 你可以往左移动 2 步到达 (1,0) 。 - 你可以往上移动 1 步到达 (0,2) 。 从入口处没法到达 (2,3) 。 所以,最近的出口是 (0,2) ,距离为 1 步。
示例 2:

输入:maze = [["+","+","+"],[".",".","."],["+","+","+"]], entrance = [1,0] 输出:2 解释:迷宫中只有 1 个出口,在 (1,2) 处。 (1,0) 不算出口,因为它是入口格子。 初始时,你在入口与格子 (1,0) 处。 - 你可以往右移动 2 步到达 (1,2) 处。 所以,最近的出口为 (1,2) ,距离为 2 步。
示例 3:

输入:maze = [[".","+"]], entrance = [0,0] 输出:-1 解释:这个迷宫中没有出口。
提示:
maze.length == mmaze[i].length == n1 <= m, n <= 100maze[i][j]要么是'.',要么是'+'。entrance.length == 20 <= entrancerow < m0 <= entrancecol < nentrance一定是空格子。
class Solution {
public:
int nearestExit(vector<vector<char>>& maze, vector<int>& entrance) {
}
};解析代码
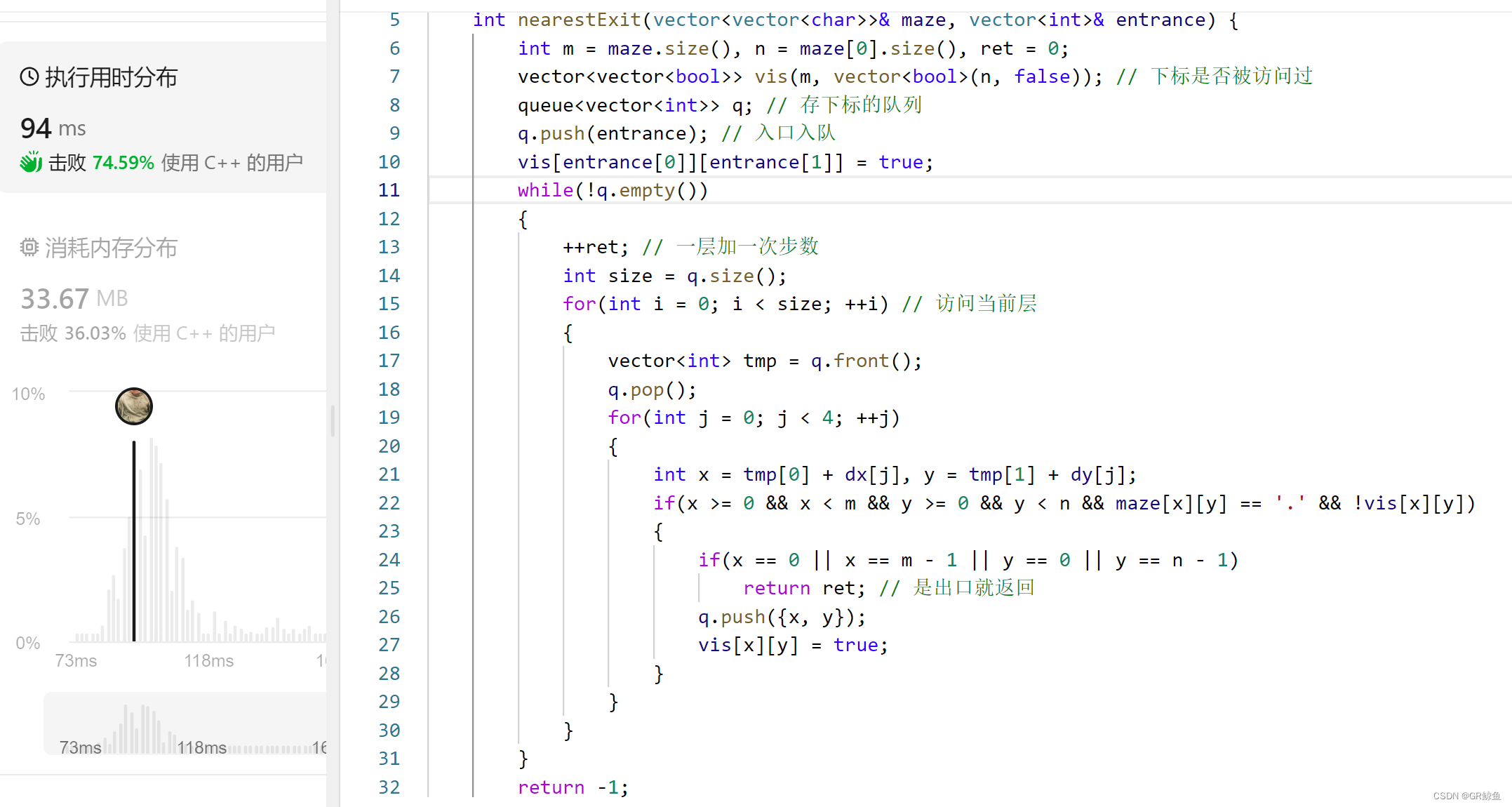
利用层序遍历来解决迷宫问题,是最经典的做法。我们可以从起点开始层序遍历,并且在遍历的过程中记录当前遍历的层数。这样就能在找到出口的时候,得到起点到出口的最短距离。
class Solution {
int dx[4] = {0, 0, -1, 1};
int dy[4] = {1, -1, 0, 0};
public:
int nearestExit(vector<vector<char>>& maze, vector<int>& entrance) {
int m = maze.size(), n = maze[0].size(), ret = 0;
vector<vector<bool>> vis(m, vector<bool>(n, false)); // 下标是否被访问过
queue<vector<int>> q; // 存下标的队列
q.push(entrance); // 入口入队
vis[entrance[0]][entrance[1]] = true;
while(!q.empty())
{
++ret; // 一层加一次步数
int size = q.size();
for(int i = 0; i < size; ++i) // 访问当前层
{
vector<int> tmp = q.front();
q.pop();
for(int j = 0; j < 4; ++j)
{
int x = tmp[0] + dx[j], y = tmp[1] + dy[j];
if(x >= 0 && x < m && y >= 0 && y < n && maze[x][y] == '.' && !vis[x][y])
{
if(x == 0 || x == m - 1 || y == 0 || y == n - 1)
return ret; // 是出口就返回
q.push({x, y});
vis[x][y] = true;
}
}
}
}
return -1;
}
};








![[计算机效率] 时间记录工具:ManicTime](https://img-blog.csdnimg.cn/direct/1a14a747e6014a24a2e023fed6f39357.png)