静电场可能分布于填充了各种媒质的区域。虽然媒质宏观上保持电中性,但其内部的各种微观带电系统不可避免地会与静电场相互作用。
一般而言,媒质可分为三类:导体、介质(绝缘体)和半导体。在静电场中半导体特性与导体类似,因此仅就导体和介质进行分析。
静电场中的导体
导体:内部含有大量的自由电子,自由电子不受原子核束缚。
特点
1、导体内电场强度处处为0
自由电子在外电场作用下,向导体表面运动。于是导体表面一侧为正电荷,一侧为负电荷,表面上的感应电荷形成一个附加电场,与外电场方向相反,最终两场强达到静电平衡。
导体内部不可能有净电荷存在,即导体内部的正负电荷必然相互抵消。
2、导体是等位体,导体表面是等位面。
3、导体表面上的电场强度垂直于导体表面。
电偶极子
电偶极子:指距离很近的一对等量异号的点电荷。
电偶极子在外电场中受力矩作用而旋转,使其电偶极矩转向外电场方向。电偶极矩就是电偶极子在单位外电场下可能受到的最大力矩,故简称电矩。
电偶极子产生的电位
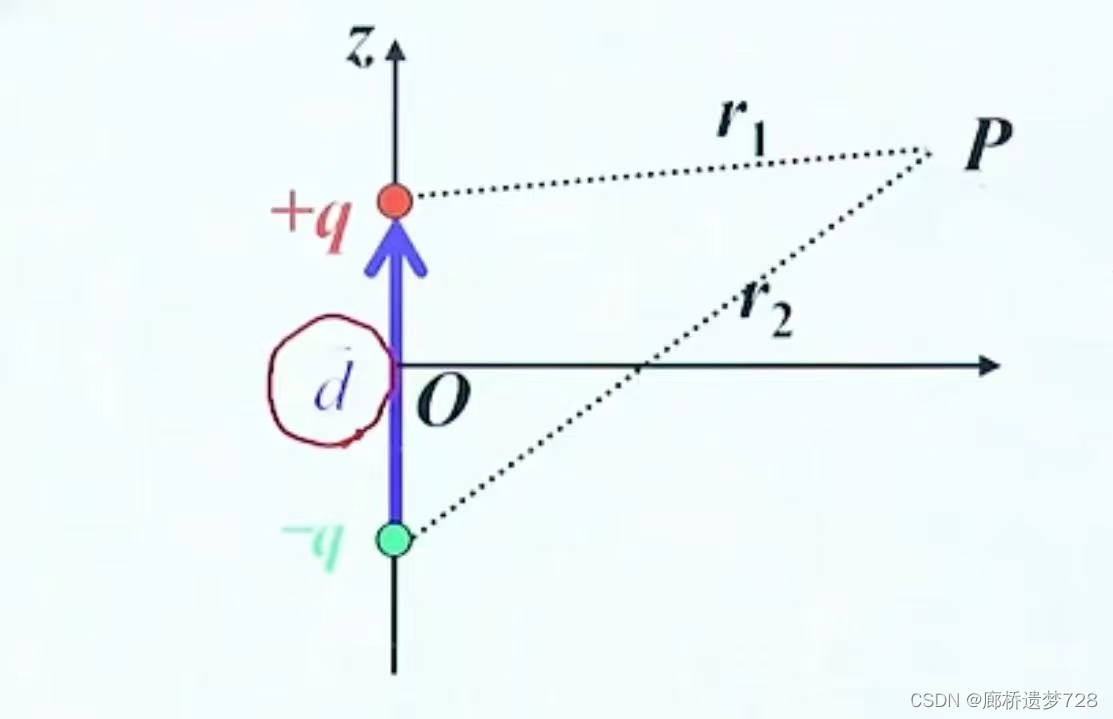
当距离足够远时:
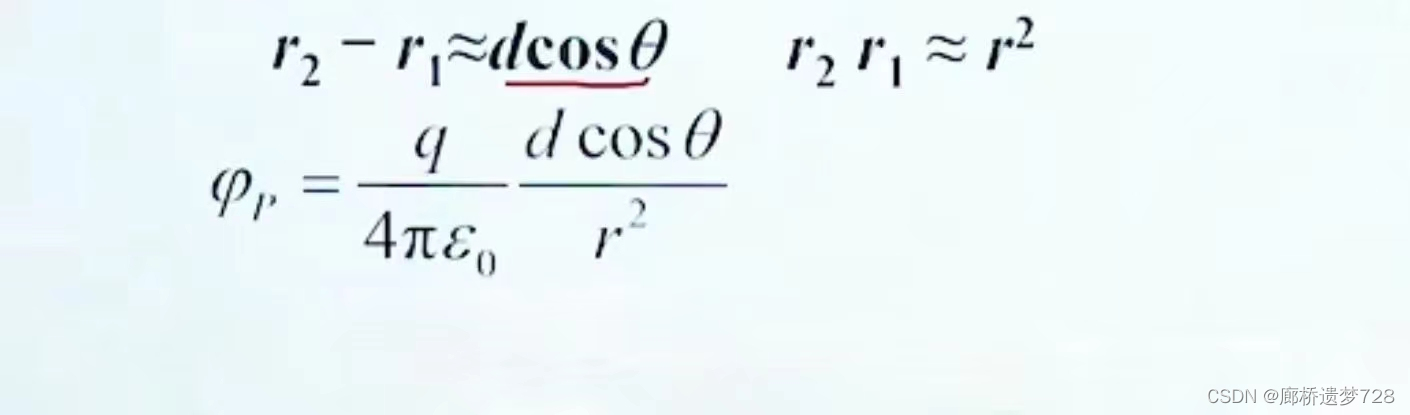
电偶极矩:
则:

静电场中的电介质
电介质:其电荷为束缚电荷(受到原子核束缚很紧密,不能脱离原子核运动,只能做微小运动)。
非极性分子:原子核(正电)和电子云(负电)作用中心一致。即在无外场作用下,无极性分子电介质不显电性。
若添加一个外电场,正电荷作用中心与负电荷作用中心产生偏移(形成电偶极子),此时电介质显电性,此过程称为位移极化。
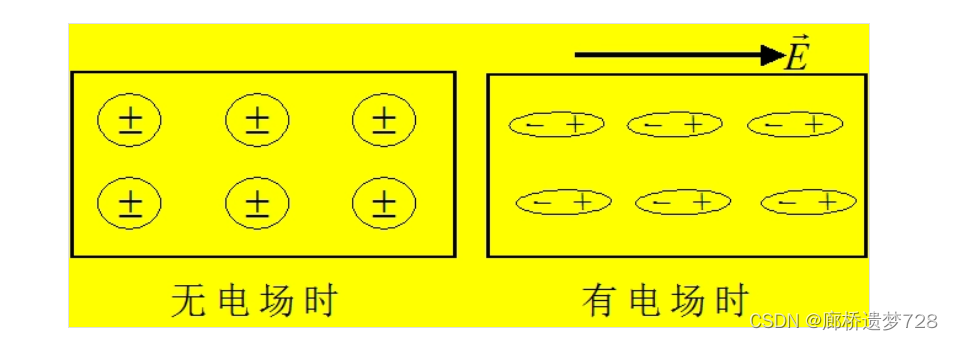
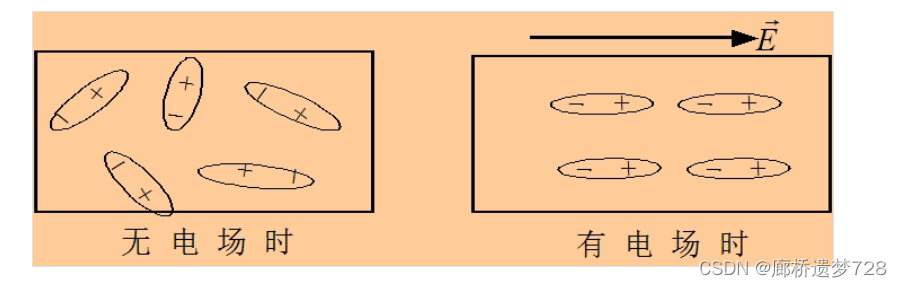
有极性分子:在无外电场作用下,正电荷和负电荷的作用中心就已经不一致了,且由于热运动,它们在空间的取向是任意的。从宏观上看有极性分子电介质不显电性。
在外电场作用下,电偶极子相当于受到转矩,所有电偶极子整齐排列,此时相互作用力不再抵消,宏观上显电性。此过程称为转向极化。
极化强度
不同物质在同一外电场作用下极化程度不同;同一物质在不同外电场作用下极化程度也不同。为了描述极化的程度,引入极化强度。
极化强度:极化介质内部单位体积内所有电偶极子的电偶极矩的矢量和。
显然实质为电偶极矩的体密度。
极化电介质的电位
由电位公式,进行推导:
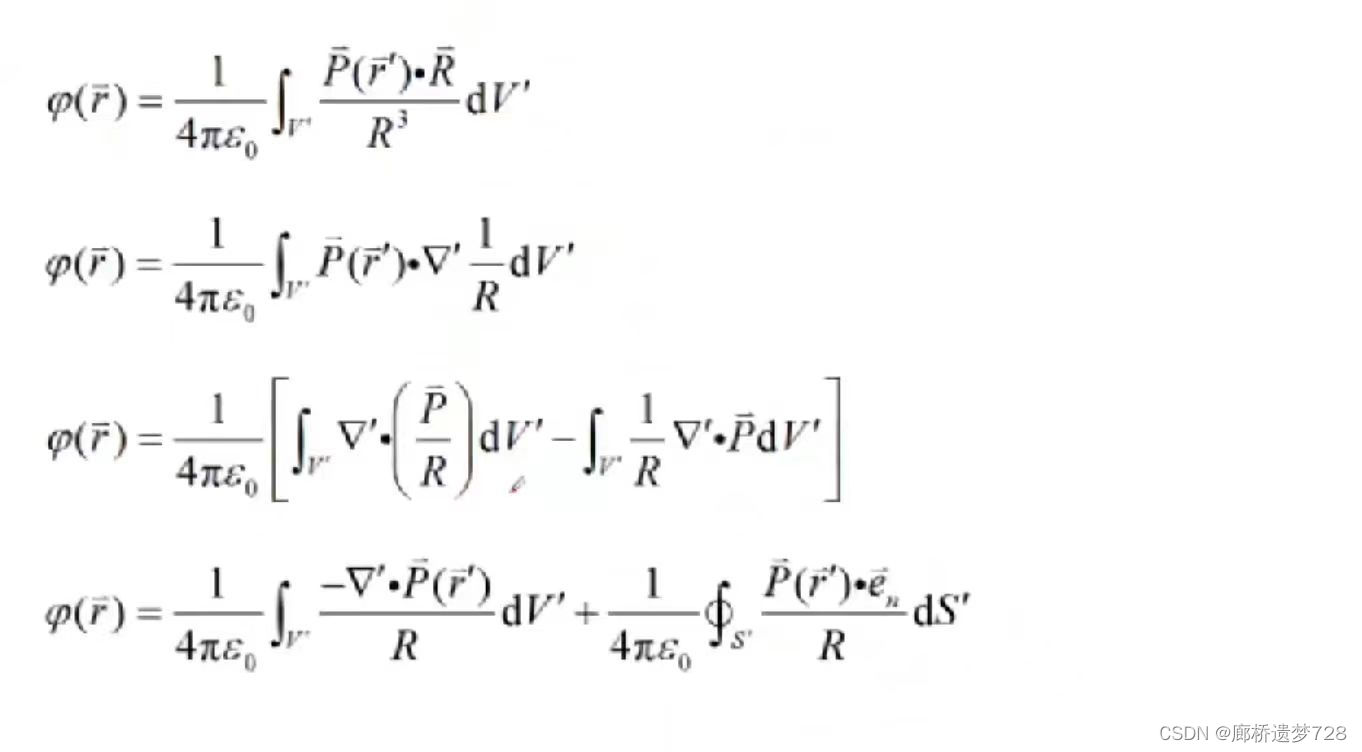
将记作
,为体极化电荷;将
记作
,为面极化电荷。
极化电介质产生的电位,等于面极化电荷与体极化电荷共同在真空中产生的电位。