文章目录

一、AcWing 4261.孤独的照片（简单）
- 1. 实现思路
- 2. 实现代码
二、AcWing 3400.统计次数（简单）
- 1. 实现思路
- 2. 实现代码
三、AcWing 4366. 上课睡觉（简单）
- 1. 实现思路
- 2. 实现代码
四、AcWing 3443. 学分绩点（简单）
- 1. 实现思路
- 2. 实现代码
五、AcWing 4818. 奶牛大学（简单）
- 1. 实现思路
- 2. 实现代码

一、AcWing 4261.孤独的照片（简单）

题目描述

Farmer John 最近购入了 N 头新的奶牛，每头奶牛的品种是更赛牛（Guernsey）或荷斯坦牛（Holstein）之一。
奶牛目前排成一排，Farmer John 想要为每个连续不少于三头奶牛的序列拍摄一张照片。
然而，他不想拍摄这样的照片，其中只有一头牛的品种是更赛牛，或者只有一头牛的品种是荷斯坦牛——他认为这头奇特的牛会感到孤立和不自然。
在为每个连续不少于三头奶牛的序列拍摄了一张照片后，他把所有「孤独的」照片，即其中只有一头更赛牛或荷斯坦奶牛的照片，都扔掉了。
给定奶牛的排列方式，请帮助 Farmer John 求出他会扔掉多少张孤独的照片。
如果两张照片以不同位置的奶牛开始或结束，则认为它们是不同的。

输入格式

输入的第一行包含 N。
输入的第二行包含一个长为 N 的字符串。如果队伍中的第 i 头奶牛是更赛牛，则字符串的第 i 个字符为 G。否则，第 i 头奶牛是荷斯坦牛，该字符为 H。

输出格式

输出 Farmer John 会扔掉的孤独的照片数量。

数据范围

3 ≤ N ≤ 5×1e5

输入样例

5
GHGHG

输出样例

3

样例解释

这个例子中的每一个长为 3 的子串均恰好包含一头更赛牛或荷斯坦牛——所以这些子串表示孤独的照片，并会被 Farmer John 扔掉。
所有更长的子串（GHGH、HGHG 和 GHGHG）都可以被接受。

具体实现

1. 实现思路

由于数据范围是 50 万，因此，我们需要使用 long long，数据范围要控制在 O(nlogn) 或者 O(n)。
要枚举的字符串当中，某个字母只能出现一次。因此，我们可以枚举只出现一次的字母是哪个，这里以字母 G 为例，枚举包含字母 G 且只包含一个 G 且字符串长度大于等于 3。
为了方便，我们可以统计出 G 左边和右边各有多少个 H，这里假设 G 左边有 L 个 H，右边有 R 个 H，便有如下几种情况。
（1）左右两边至少各包含一个 H ，则需要丢弃的照片数为 L*R。
（2）左边没有 H，右边至少包含两个 H，则需求丢弃的照片数为 R-1。
（3）右边没有 H，左边至少包含两个 H，则需求丢弃的照片数为 L-1。
将如上三种情况相加，便可以得到总共需要丢弃的照片数。

2. 实现代码

#include <bits/stdc++.h>
using namespace std;

typedef long long LL;

const int N = 500010;

int n;
char str[N];
//L[N]表示左边有多少个跟当前位置不同的字母
//R[N]表示右边有多少个跟当前位置不同的字母
int L[N], R[N];

int main()
{
    cin >> n;
    cin >> str;
    
    //左边
    for (int i = 0, h = 0, g = 0; i < n; i ++ )
    {
    	if (str[i] == 'G')
		{
			L[i] = h;
			h = 0;
			g ++;
		}
        else
		{
			L[i] = g;
			g = 0;
			h ++;
		}
	}
	
    //右边
    for (int i = n - 1, h = 0, g = 0; i >= 0; i -- )
    {
    	if (str[i] == 'G')
		{
			R[i] = h;
			h = 0;
			g ++;
		}
        else
		{
			R[i] = g;
			g = 0;
			h ++;
		}
	}        

    LL res = 0;
    
    for (int i = 0; i < n; i ++ )
    {
    	res += (LL)L[i] * R[i] + max(L[i] - 1, 0) + max(R[i] - 1, 0);
	}        

    cout << res;
    system("pause");
    return 0;
}

二、AcWing 3400.统计次数（简单）

题目描述

给定两个正整数 n 和 k，求从 1 到 n 这 n 个正整数的十进制表示中 k 出现的次数。

输入格式

共一行，包含两个整数 n 和 k。

输出格式

输出一个整数，表示答案。

数据范围

1 ≤ n ≤ 1e6
1 ≤ k ≤ 9

输入样例

12 1

输出样例

5

样例解释

从 1 到 12 这些整数中包含 1 的数字有 1,10,11,12，一共出现了 5 次 1。

具体实现

1. 实现思路

该题的数据范围比较小，因此，我们可以使用暴力枚举进行解决。
我们可以从 1 遍历到 n，分别统计每个数中 k 出现的次数。
怎么统计一个数 x 中 k 出现的次数呢？我们可以不断取 x 的末尾，判断它是否为 k，再把 x 除以 10（舍弃末位）。
这样一直把函数结果累加到答案上，最后输出答案即可。

2. 实现代码

#include <bits/stdc++.h>
using namespace std;

int main()
{
    int n, k;
    cin >> n >> k;

    int res = 0;
    for (int i = 1; i <= n; i ++ )
    {
        for (int j = i; j; j /= 10)
        {
            if (j % 10 == k)
            {
                res ++ ;
            }
        }
    }
    
    cout << res << endl;
    system("pause");
    return 0;
}

三、AcWing 4366. 上课睡觉（简单）

题目描述

有 N 堆石子，每堆的石子数量分别为 a₁,a₂,…,a_N。
你可以对石子堆进行合并操作，将两个相邻的石子堆合并为一个石子堆，例如，如果 a=[1,2,3,4,5]，合并第 2,3 堆石子，则石子堆集合变为 a=[1,5,4,5]。
我们希望通过尽可能少的操作，使得石子堆集合中的每堆石子的数量都相同。
请你输出所需的最少操作次数。
本题一定有解，因为可以将所有石子堆合并为一堆。

输入格式

第一行包含整数 T，表示共有 T 组测试数据。
每组数据第一行包含整数 N。
第二行包含 N 个整数 a₁,a₂,…,a_N。

输出格式

每组数据输出一行结果。

数据范围

1 ≤ T ≤ 10
1 ≤ N ≤ 1e5
0 ≤ a_i ≤ 1e6
从 i=1 到 i=n 的 a_i 之和 ≤ 1e6
每个输入所有 N 之和不超过 1e5

输入样例

3
6
1 2 3 1 1 1
3
2 2 3
5
0 0 0 0 0

输出样例

3
2
0

样例解释

第一组数据，只需要用 3 个操作来完成：

1 2 3 1 1 1
-> 3 3 1 1 1
-> 3 3 2 1
-> 3 3 3

第二组数据，只需要用 2 个操作来完成：

2 2 3
-> 2 5
-> 7

第三组数据，我们什么都不需要做。

具体实现

1. 实现思路

假设每堆石子有 cnt 个，一共有 sum 个石子。
如果我们想让每堆石子的数量相同，那么，sum 除以 cnt 一定是可以整除的。然后，我们在所有可以取到的 cnt 里面，找一个操作数量最少的即可。
假设我们初始有 n 堆石子，最后，每一堆有 cnt 个石子，那么会有 sum / cnt 堆石子，每操作一次会减少一堆，因此，我们一共有 n - sum / cnt 次操作。
我们需要操作次数越少越好，但是，最初有多少堆石子和总共有多少个石子是定好的。所以，我们只能让每堆石子的数量 cnt 越小越好。然后，分别判断这个 cnt 是否成立即可。
关于判断 cnt 是否成立，也就是我们判断最后能否将每堆的数量变成 cnt，由于只能合并相邻两堆。所以，问题就转变为，能否将整个序列分成若干段，使得每一段中的石子总数是 cnt。
对此，我们从前向后考虑，逐步枚举。当我们第一段的石子数量小于 cnt 时，就说明还需要加入新的一堆石子，直到第一段的石子数量变成大于等于 cnt 为止。
第一种情况：当我们的第一段石子数量大于 cnt 时，说明无解。因为，不加入下一堆石子数量小于 cnt，加入下一堆石子数量大于 cnt，说明第一段石子的数量是无法等于 cnt 的。
第二种情况：当我们的第一段石子数量等于 cnt 时，如果下一堆石子数量是 0 的话，那是否加入则无所谓；如果下一堆石子数量不是 0 的话，则千万不能加入。

2. 实现代码

#include <bits/stdc++.h>

using namespace std;

const int N = 100010;

int n;
//w[N]表示每堆石子的数量
int w[N];

bool check(int cnt)
{
    //s表示这一段石子的数量
    for (int i = 0, s = 0; i < n; i ++ )
    {
        s += w[i];

        //如果s大于cnt，就直接返回false，开始枚举下一个
        //如果s等于cnt，就将其置为0，最后返回true，表明可以实现。
        if (s > cnt) 
		{
			return false;
		}
        if (s == cnt)
		{
			s = 0;
		}
    }
    return true;
}

int main()
{
    int T;
    cin >> T;
    
    while (T -- )
    {
        cin >> n;
        int sum = 0;
        
        for (int i = 0; i < n; i ++ )
        {
            cin >> w[i];
            sum += w[i];
        }

        for (int i = n; i; i -- )
		{
			if (sum % i == 0 && check(sum / i))
            {
                cout << n - i << endl;
                break;
            }
		}            
    }
    
    system("pause");
    return 0;
}

四、AcWing 3443. 学分绩点（简单）

题目描述

北京大学对本科生的成绩施行平均学分绩点制（GPA）。
既将学生的实际考分根据不同的学科的不同学分按一定的公式进行计算。
公式如下：

实际成绩	绩点
90——100	4.0
85——89	3.7
82——84	3.3
78——81	3.0
75——77	2.7
72——74	2.3
68——71	2.0
64——67	1.5
60——63	1.0
60以下	0

一门课程的学分绩点 = 该课绩点 × 该课学分
总评绩点 = 所有学科学分绩点之和 / 所有课程学分之和
现要求你编写程序求出某人 A 的总评绩点（GPA）。

输入格式

第一行，总的课程数 n；
第二行，相应课程的学分（两个学分间用空格隔开）；
第三行，对应课程的实际得分；
此处输入的所有数字均为整数。

输出格式

输出有一行，总评绩点，精确到小数点后 2 位小数。

数据范围

1 ≤ n ≤ 10
学分取值范围 [1,10]
课程得分范围 [0,100]

输入样例

5
4 3 4 2 3
91 88 72 69 56

输出样例

2.52

具体实现

1. 实现思路

该题可以通过暴力方法直接完成，通过 if 判断语句，得出课程的实际得分所对应的绩点，再将其与该课程的学分相乘得到学分绩点，最后累加，再除以总学分之和即可，这要注意要保留两位小数。
在 C++ 代码当中，保留小数需要使用头文件 #include <iomanip>，输出语句使用如下前缀 cout << fixed << setprecision(2) ，括号中表示保留小数的位数。
在本题中，为了简便，我们使用两个数组，分别用来存成绩的区间下界和该区间对应的学分，便于我们后面的直接判断。

2. 实现代码

#include <bits/stdc++.h>

using namespace std;

const int N = 20;

int key[10] = {0, 60, 64, 68, 72, 75, 78, 82, 85, 90};
double value[10] = {0, 1.0, 1.5, 2.0, 2.3, 2.7, 3.0, 3.3, 3.7, 4.0};

//a[N]表示相应课程的学分
//b[N]对应课程的实际得分 
int a[N], b[N];

double get(int x)
{
    for (int i = 9; i >= 0; i -- )
    {
    	if (x >= key[i])
        {
        	return value[i];
		}
	}            
    return 0;
}

int main()
{
    int n;
    cin >> n;

    for (int i = 0; i < n; i ++ )
	{
		cin >> a[i];
	}
	
    for (int i = 0; i < n; i ++ )
	{
		cin >> b[i];
	}

    double sum = 0, cnt = 0;
    
    for (int i = 0; i < n; i ++ )
    {
        sum += get(b[i]) * a[i];
        cnt += a[i];
    }

    cout << fixed << setprecision(2) << sum / cnt;
    system("pause");
    return 0;
}

五、AcWing 4818. 奶牛大学（简单）

题目描述

Farmer John 计划为奶牛们新开办一所大学！
有 N 头奶牛可能会入学。
每头奶牛最多愿意支付 c_i 的学费。
Farmer John 可以设定所有奶牛入学需要支付的学费。
如果这笔学费大于一头奶牛愿意支付的最高金额，那么这头奶牛就不会入学。
Farmer John 想赚尽可能多的钱，从而可以给他的讲师提供一笔可观的工资。
请求出他能赚到的钱的数量，以及此时应当收取多少学费。

输入格式

输入的第一行包含 N。
第二行包含 N 个整数 c₁,c₂,…,c_N，其中 c_i 是奶牛 i 愿意支付的最高学费金额。

输出格式

输出 Farmer John 可以赚到的最大金额以及最优情况下他应该收取的学费。如果有多个解，输出收取学费最小的解。
注意这个问题涉及到的整数可能需要使用 64 位整数型（例如，Java 中的 “long”，C/C++ 中的 “long long”）。

数据范围

1 ≤ N ≤ 1e5
1 ≤ c_i ≤ 1e6

输入样例

4
1 6 4 6

输出样例

12 4

样例解释

如果 Farmer John 收费 4，那么 3 头奶牛将会入学，从而使他赚取 3×4=12 的金额。

具体实现

1. 实现思路

由于我们设定的学费不同，愿意交学费的奶牛数量也不同，要综合比较选取赚到的最大金额以及最优情况下应该收取的学费。如果有多个解，输出收取学费最小的解。
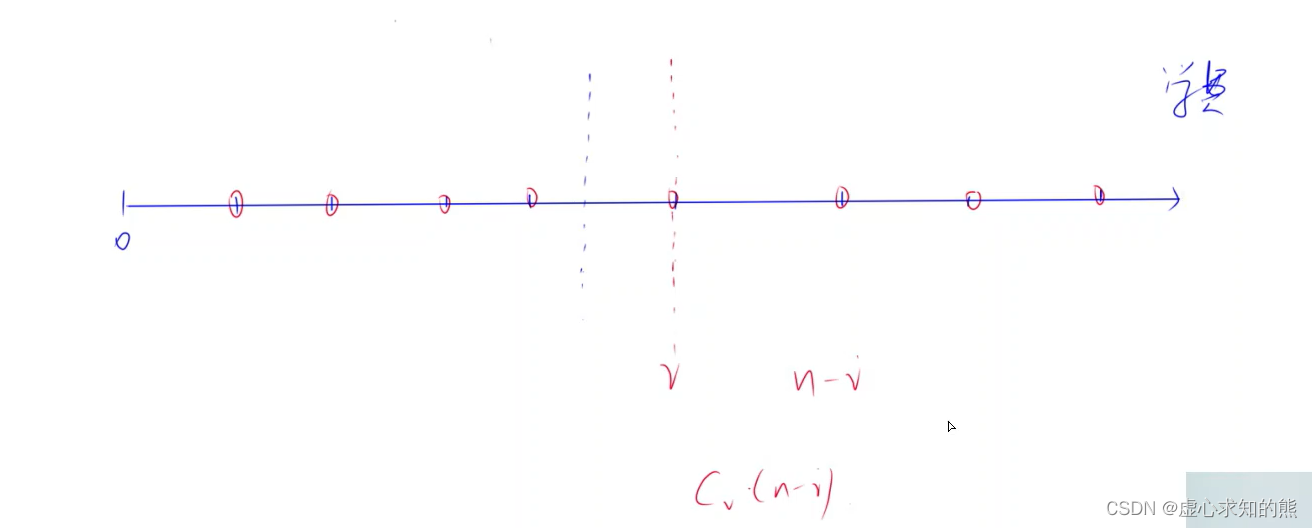
为了方便，我们可以先将愿意支付学费的奶牛从小到大排序。
那么，取在一个区间里的学费数量与取在该区间右端点，收取的总体金额是相同的。
因此，我们枚举每一个点，该点所收取的总体金额就是该点表示的学费乘以右边点的个数。
最后，在其中选取一个总体金额最大的值，如果有总体金额相同的，则选取学费小的（也就是靠左边的点）。

在这里插入图片描述

2. 实现代码

#include <bits/stdc++.h>
using namespace std;

typedef long long LL;

const int N = 100010;

int n;
int w[N];

int main()
{
    cin >> n;
    for (int i = 0; i < n; i ++ )
	{
		cin >> w[i];
	}
    
    //将所有牛愿意交的学费按从小到大排序
    sort(w, w + n);

    //将总金额和入学费用初始化为0
    LL rtot = 0, rfee = 0;
    for (int i = 0; i < n; i ++ )
    {
        //该点的总金额
        LL tot = (LL)w[i] * (n - i);

        //如果有两个总金额相同的，我们要输出收学费少的。
        //因此，可以直接略去。
        //因为，学费是按从小到大排列，在左边的学费自然比在右边的学费少。
        if (tot > rtot)
        {
            rtot = tot;
            rfee = w[i];
        }
    }

    cout << rtot << " " << rfee << endl;
	system("pause"); 
	return 0;
}