题目
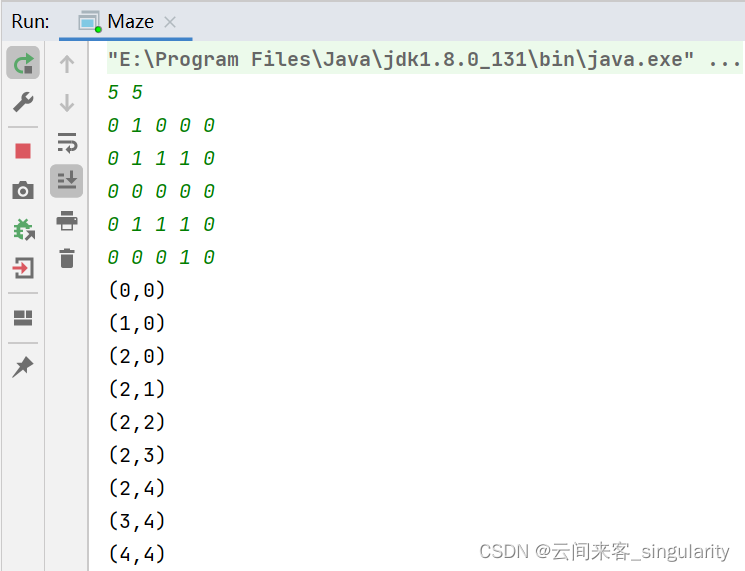
定义一个二维数组 N*M,如 5 × 5 数组如下所示:
int maze[5][5] = {
0, 1, 0, 0, 0,
0, 1, 1, 1, 0,
0, 0, 0, 0, 0,
0, 1, 1, 1, 0,
0, 0, 0, 1, 0,
};
它表示一个迷宫,其中的1表示墙壁,0表示可以走的路,只能横着走或竖着走,不能斜着走,要求编程序找出从左上角到右下角的路线。入口点为[0,0],第一格是可以走的路。
数据范围:2 <= n, m <= 10, 输入的内容只包含0 <= val <= 1。
输入描述:
输入两个整数,分别表示二维数组的行数,列数。再输入相应的数组,其中的1表示墙壁,0表示可以走的路。数据保证有唯一解,不考虑有多解的情况,即迷宫只 有一条通道。
输出描述:
左上角到右下角的最短路径,格式如样例所示。


思路:广度优先遍历矩阵BFS
深度优先遍历(DFS)和广度优先遍历(BFS)
图的遍历是指,从给定图中任意指定的顶点(称为初始点)出发,按照某种搜索方法沿着图的边访问图中的所有顶点,使每个顶点仅被访问一次,这个过程称为图的遍历。遍历过程中得到的顶点序列称为图遍历序列。
图的遍历过程中,根据搜索方法的不同,又可以划分为两种搜索策略:
- 深度优先搜索(DFS,Depth-First-Search)
- 广度优先搜索(BFS,Breadth-First-Search)
实现深度优先遍历的关键在于回溯,实现广度优先遍历的关键在于回放。
1.深度优先遍历(DFS)——栈
主要思路是从图中一个未访问的顶点v开始,沿着一条路一直走到底,然后从这条路尽头的节点回退到上一个节点,再从另一条路开始走到底…,不断递归重复此过程,直到所有的顶点都遍历完成,它的特点是不撞南墙不回头,先走完一条路,再换一条路继续走。类似于树的前,中,后序遍历。
2. 广度优先遍历(BFS)——队列
设初始状态时图中的所有顶点未被访问,首先访问图中某指定的起始顶点v,并将其标记为已访问过,然后由v出发依次访问v的各个未被访问的邻接点v1,v2,…,vk;并将其均标识为已访问过,再分别从v1,v2,…,vk出发依次访问它们未被访问的邻接点,并使“先被访问顶点的邻接点”先于“后被访问顶点的邻接点”被访问。直至图中所有与顶点v路径相通的顶点都被访问到。类似于树的层序遍历。
代价相同的图中,广度优先遍历可以保证遍历到的目标点就是经过最短路径到达的点。为此可以创建一个Point类,属性为横纵坐标和父节点。从(0,0)出发,将经过的坐标点都设为1,避免重复经过而进入死循环。把当前点的上下左右值为0的点都加入队列中,直到遇见出口为止。遇到出口时,pos的father路径就是最短路径的逆路径。此时只需要把逆路径反转一下即可。(利用递归可以后序输出链表的特性,可以省去反转路径的操作)
代码
import java.util.*;
class Point {
int px;
int py;
Point father;
Point(int px, int py, Point father) {
this.px = px;
this.py = py;
this.father = father;
}
Point() {}
}
public class Maze {
public static void print(Point p) {
if(p != null){
print(p.father);
System.out.println("(" + p.px + "," + p.py + ")");
}
}
public static void main(String args[]) {
Scanner sc = new Scanner(System.in);
while(sc.hasNextInt()) {
int row = sc.nextInt();
int col = sc.nextInt();
int [][] grid = new int[row][col];
for(int i = 0; i < row; ++i) {
for(int j = 0; j < col; ++j) {
grid[i][j] = sc.nextInt();
}
}
Queue<Point> que = new LinkedList<>();
que.offer(new Point(0, 0, null));
grid[0][0] = 1;
Point pos = null;
while(true) {
pos = que.poll();
int px = pos.px;
int py = pos.py;
if(px == row - 1 && py == col - 1) {
break;
} else {
if(px + 1 < row && grid[px + 1][py] == 0) {
grid[px + 1][py] = 1;
que.offer(new Point(px + 1, py, pos));
}
if(py - 1 >= 0 && grid[px][py - 1] == 0) {
grid[px][py - 1] = 1;
que.offer(new Point(px, py - 1, pos));
}
if(px - 1 >= 0 && grid[px - 1][py] == 0) {
grid[px - 1][py] = 1;
que.offer(new Point(px - 1 ,py, pos));
}
if(py + 1 < col && grid[px][py + 1] == 0) {
grid[px][py + 1] = 1;
que.offer(new Point(px, py + 1, pos));
}
}
}
print(pos);
}
}
}