引言
本文根据实验楼以及自己查询到的一些资料(文末给出),模拟了一下区块链从诞生到交易的整个过程,也算是弥补了一下之前区块链的一些缺失知识。
哈希加密原理介绍
什么是比特币?
比特币是一种加密货币,也是一种分布式数字货币。它的创建者使用匿名身份被称为"中本聪"。比特币是通过对一组特定的数据进行加密来创建的,这些数据被称为"区块链"。比特币使用密码学技术来确保货币交易的安全性和不可更改性,这意味着比特币交易是不可篡改的。比特币是完全去中心化的,意味着它不受任何政府或金融机构的控制,并且可以在互联网上以匿名方式进行交易。
而这种去中心化,通过加密匿名方式来进行交易中最基本的原理,则是哈希加密,那么下面将介绍几种主要的hash加密方式。
单向散列函数介绍
单向散列函数是一项为数字信息提取「指纹」的技术,而提取出的「指纹」信息称为散列值。

单向散列函数具有以下几个特性:
-
散列值固定
- 值本身是固定的,只要数据信息的内容不发生改变,使用固定的单向散列函数计算出来的散列值就是固定的,每次计算得到的都是这个值而不会发生改变;
- 散列值的长度是固定的,固定的单向散列函数计算出来的散列值长度都是固定的,并且长度与数字信息的长度无关。
-
单向性
我们很容易根据数字信息计算出散列值,却无法通过散列值反算出数字信息。散列算法可以理解为是一种有损压缩算法,我们无法从计算结果还原原始信息,这点与加密算法有着本质的区别。
-
强抗碰撞性
两个不同的数字信息通过单向散列函数得到相同的散列值,这种情况,我们称为散列碰撞。而所谓的强抗碰撞性,则指的是针对某一单向散列函数,我们要找到具备相同散列值的两条不同的数字信息非常的困难。这个特性经常用来衡量一个单向散列函数的安全性。如果说某个单向散列函数的抗碰撞性被攻破,那就说明这个单向散列函数必须被抛弃或者谨慎使用。

-
加盐防碰撞
盐(Salt),在密码学中,是指在散列之前将散列内容(例如:密码)的任意固定位置插入特定的字符串。这个在散列中加入字符串的方式称为“加盐”。其作用是让加盐后的散列结果和没有加盐的结果不相同,在不同的应用情景中,这个处理可以增加额外的安全性。
为了防止攻击会采用加盐的方法,原来的明文会加上一个随机数之后的 Hash 值,Hash 值和盐会保存在两个地方,只要不是同时泄漏就很难被破解
-
雪崩效应
雪崩效应指的是当输入的数字信息发生微小变化时,也会导致通过单向散列函数计算得到的散列值发生巨大的改变(并且是不可区分的)如下图就是SHA-1单向散列函数所展示的雪崩效应:

单向散列函数及其应用
单向散列函数本质上就是一种满足某种需求的算法实现,而在计算机领域里一种需求往往总能有不止一种的实现方案,单向散列函数也具有非常多的实现算法,下面我们就来介绍几种常见的单向散列函数算法:
| 算法 | 比特数 | 字节数 |
|---|---|---|
| MD4 | 128bit | 16byte |
| MD5 | 128bit | 16byte |
| SHA-1 | 160bit | 20byte |
| SHA-224 | 224bit | 28byte |
| SHA-256 | 256bit | 32byte |
| SHA-384 | 384bit | 48byte |
| SHA-512 | 512bit | 64byte |
-
MD4 、MD5
MD4是由Rivest于1990年设计的单向散列函数,能够产生128比特的散列值。不过,随着Dobbertin提出了寻找MD4散列碰撞的方法,现在它已经不安全了。
MD5是由Rivest于1991年设计的单向散列函数,能够产生128比特的散列值。不过MD5的强抗碰撞性已经被攻破,即现在已经能够产生具备相同散列值的两条不同的数据信息了,因此它也已经不再安全。
-
SHA-1 、SHA-2家族
SHA-1是由NIST设计的一种单向散列函数,它能够产生160比特的散列值。SHA-1的强抗碰撞性已经于2005年被攻破,因此也已经不再安全。
SHA-2是由SHA-256、SHA-384和SHA-512组成的单向散列函数系列,它们分别能产生256 比特、384比特和512比特的散列值,这个系列的抗碰撞性尚未被攻破,因此可以安全使用。
-
RIPEMD - 160
RIPEMD-160是于1996年由Hans Dobbertin,Antoon Bosselaers和Bart Preneel设计的一种能够产生160比特的散列值的单向散列函数。RIPEMD-160抗碰撞性尚未被攻破。
hashlib模块使用
在python中,hashlib自python2起,就成为了默认库函数,我们可以直接导入,并查看当前版本所支持的所有单向散列函数:
import hashlib
print(hashlib.algorithms_available)
"""
{'sha3_256', 'sha512', 'dsaEncryption', 'shake_256', 'whirlpool', 'dsaWithSHA', 'blake2s', 'MD5', 'md5', 'blake2b', 'sha', 'DSA-SHA', 'SHA512', 'sha3_512', 'sha1', 'ecdsa-with-SHA1', 'sha3_224', 'SHA', 'SHA384', 'MD4', 'sha256', 'RIPEMD160', 'ripemd160', 'SHA256', 'sha224', 'shake_128', 'DSA', 'sha384', 'SHA1', 'sha3_384', 'md4', 'SHA224'}
"""
选取其中几种散列函数,打印最大长度:
import hashlib
md5 = hashlib.new('md5')
s256 = hashlib.new('sha256')
r160 = hashlib.new('ripemd160')
# 打印 md5 散列值字节长度
print('The length of md5 hash value is {}'.format(md5.digest_size))
# 打印 sha256 散列值字节长度
print('The length of sha256 hash value is {}'.format(s256.digest_size))
# 打印 ripemd160 散列值字节长度
print('The length of ripemd160 hash value is {}'.format(r160.digest_size))
"""
The length of md5 hash value is 16
The length of sha256 hash value is 32
The length of ripemd160 hash value is 20
"""
然后选用sha256对当前字段进行加密,这里有两种加密方式,代码如下:
import hashlib
# 通过构造方法传入的消息的散列值
s256 = hashlib.new('sha256', b"hello world")
ret1 = s256.hexdigest()
# 通过多次 `update` 方法传入消息得到的散列值
s256 = hashlib.new('sha256')
s256.update(b"hello ")
s256.update(b"world")
ret2 = s256.hexdigest()
print("ret1: ",ret1)
print("ret2: ",ret2)
"""
ret1: b94d27b9934d3e08a52e52d7da7dabfac484efe37a5380ee9088f7ace2efcde9
ret2: b94d27b9934d3e08a52e52d7da7dabfac484efe37a5380ee9088f7ace2efcde9
"""
一种是初始化的时候就已经对字段加密,还有就是先初始化加密算法,然后将字段更新进去,因为python不存在字符与字符串的区别,所以不论单引还是双引对结果没有影响,但如果里面有任何一个符号的不同,结果就大不相同,具体就是前面提到的雪崩效应了。
以上不管是哪种加密方式,其共有的方法为:
| 名称 | 描述 |
|---|---|
| update(arg) | 可以重复利用指定了特殊加密算法的Hash对象,对arg进行加密 |
| digest(…) | 以字符形式返回加密内容 |
| hexdigest(…) | 以16进制形式返回加密内容 |
| copy(…) | 与python本身的浅拷贝copy方法一致,克隆Hash对象 |
经过上面简单使用hashlib,我们能直接拿任何一个字符串经过相应的哈希算法得到的加密表示,如果还需要提高安全性,那么就需要加盐放偷窃了,即加盐除了上面提到的防碰撞,更主要的还是保证数据传输安全,这里有个简单版本demo为:
import hashlib
import base64
import uuid
password = 'test_password'
salt = base64.urlsafe_b64encode(uuid.uuid4().bytes)
print "salt: ",salt
t_sha = hashlib.sha512()
t_sha.update(password+salt)
hashed_password = base64.urlsafe_b64encode(t_sha.digest())
print "hashed_password: ",hashed_password
"""
salt: 31yAJyX9TeySiD9AXx4GIg==
hashed_password: Omd5WwvSG2u3NFb0azXIXpzmtSlzhYHxRRkcBw3tSQxTtlDNjI4Nr9q14KfMQZXubXuJOah5PmGxL5L1zeV9aQ==
"""
上面是python2语法的一个验证,来源于十几年前的一个Stack Overflow的帖子:
https://stackoverflow.com/questions/9594125/salt-and-hash-a-password-in-python?noredirect=1&lq=1
选这个的缘由是我百度的大部分帖子都指向了这个链接,而我又不想Google了,况且该帖子确实清晰明了,需要讨论的都涉及到了,比较推荐加深理解。
另外,在python2.7中可以通过 hashlib.pbkdf2_hmac()直接实现哈希加盐:
def hash_encrpt(password):
salt = os.urandom(32) # salt
password = password.strip()
key = hashlib.pbkdf2_hmac(
'sha256', # The hash digest algorithm for HMAC
password.encode('utf-8'), # Convert the password to bytes
salt, # Provide the salt
100000, # It is recommended to use at least 100,000 iterations of SHA-256
dklen=128 # Get a 128 byte key
)
return salt,key
这里我稍微改了改,python3的版本为:
from hashlib import sha256
import random
import string
# 获取由4位随机大小写字母、数字组成的salt值
def create_salt(length = 4):
chars = 'AaBbCcDdEeFfGgHhIiJjKkLlMmNnOoPpQqRrSsTtUuVvWwXxYyZz0123456789'
salt = [random.choice((string.ascii_letters + string.digits)) for i in range(length)]
return ("".join(salt))
# 获取原始密码+salt的sha256值
def create_sha256_value(pwd,salt):
ssha256 = sha256()
ssha256.update((pwd+salt).encode('utf-8'))
return ssha256.hexdigest()
# 随机密码
pwd = input("请输入密码:")
print("密码为:",pwd)
# 随机生成的4位salt
salt = create_salt()
print("salt为:",salt)
# 加密后的密码
sha256_pwd = create_sha256_value(pwd,salt)
print("加盐哈希值为:",sha256_pwd)
"""
请输入密码:321
密码为: 321
salt为: wLbZ
加盐哈希值为: f319d21267f2c1a1a35742ea29f93cae8a53f3e222d8cf1bda38e72e257b9f71
"""
一般如果是做简单web应用或者注册功能等,会将salt与除密码外的其它用户特征信息保存到数据库,然后当下一次登录的时候,取出相应信息经过同样字段的hash值token,与前端保存的做对比。或者在python框架里,django和flask其实都是有secret_key的,虽然我很久没写web了,但还是记得一点jwt原理,基本secret_key很难被盗用,顺带回头复习了一波jwt,emmm(restframework(4):JWT)
当然hashlib只是最简单也是最通用的一种方式,如果需要在更加安全的包进行生产环境,上面分享的Stack Overflow中第二位高赞即使用bcrypt:
def get_hashed_password(plain_text_password):
# Hash a password for the first time
# (Using bcrypt, the salt is saved into the hash itself)
return bcrypt.hashpw(plain_text_password, bcrypt.gensalt())
def check_password(plain_text_password, hashed_password):
# Check hashed password. Using bcrypt, the salt is saved into the hash itself
return bcrypt.checkpw(plain_text_password, hashed_password)
根据我查到的资料上看,还有一种crypt算法,这两者的区别是crypt算法基本不再使用了,之前不带参数的crypt是标准的UNIX密码哈希函数移植到PHP,而bcrypt基于Blowfish算法。后者在内部会使用内存初始化 hash 过程,由于需要内存,虽然在 CPU 上运行很快,但在 GPU 并行运算却不快,这也减缓了攻击者的破解速度。(因为对于攻击者减缓了每次生成新的key的时间)
具体实现过程可参考,这里就不再详述:
密码学系列之:bcrypt加密算法详解
RSA 算法介绍
RSA 加密算法是一种非对称加密算法。在公开密钥加密和电子商业中 RSA 被广泛使用。RSA 是 1977 年由罗纳德 · 李维斯特(Ron Rivest)、阿迪 · 萨莫尔(Adi Shamir)和伦纳德 · 阿德曼(Leonard Adleman)一起提出的。RSA 就是他们三人姓氏开头字母拼在一起组成的。
RSA 算法的可靠性由极大整数因数分解的难度决定。换言之,对一极大整数做因数分解愈困难,RSA 算法愈可靠。假如有人找到一种快速因数分解的算法的话,那么用 RSA 加密的信息的可靠性就肯定会极度下降。但找到这样的算法的可能性是非常小的。如今,只有短的 RSA 密钥才可能被强力方式解破。到 2017 年为止,还没有任何可靠的攻击 RSA 算法的方式。
来源:CTF-wiki
公钥加密
公钥加密是一种防止数据在传输过程中被窃取后能被窃取者轻易读懂信息的技术,这里有四个概念:
- 明文,指的就是原始的需要进行传输的数据信息;
- 密文,指的是明文经过加密处理后的数据形态;
- 密钥,指的是将明文转换为密文或者将密文转换为明文过程中,起到关键作用的一段秘密数据信息;
- 加密/解密算法,加密算法就是将明文转换为密文的算法,解密算法将密文转化为明文的算法。
其中公钥和私钥产生的原理为:
- 随机选择两个不同大质数 p p p 和 q q q,计算 N = p × q N = p \times q N=p×q
- 根据欧拉函数,求得 φ ( N ) = φ ( p ) φ ( q ) = ( p − 1 ) ( q − 1 ) \varphi (N)=\varphi (p)\varphi (q)=(p-1)(q-1) φ(N)=φ(p)φ(q)=(p−1)(q−1)
- 选择一个小于 φ ( N ) \varphi (N) φ(N)的整数 e e e,使 e e e 和 φ ( N ) \varphi (N) φ(N)互质。并求得 e e e 关于 φ ( N ) \varphi (N) φ(N) 的模反元素,命名为 d d d, 有 e d ≡ 1 ( m o d φ ( N ) ) ed\equiv 1 \pmod {\varphi (N)} ed≡1(modφ(N))
- 将 p p p 和 q q q 的记录销毁
此时, ( N , e ) (N,e) (N,e) 是公钥, ( N , d ) (N,d) (N,d) 是私钥。
之后关于加密与解密的数学推导就不再这里引述,感兴趣的可以去看CTF-wiki关于解密正确性的证明过程。
这里根据公钥和私钥的产生过后,那么就有两种加密算法,分别为对称加密与非对称加密。
-
对称加密

根据图片,很好理解,对称加密的 “对称” 就是指加密和解密使用同一个密钥,对称密钥又称为共享密钥(Pre-Shared key,PSK)。由于对称加密只有一个密钥,因此一定要保证密钥的安全,才能保证通信的机密性。 -
非对称加密

非对称加密也叫公钥加密算法。它的 “不对称” 在于它有两个密钥,一个叫 “公钥”,可以交付给任何人(往往通过数字证书的方式交付),另一个叫 “私钥”,必须严格保密,公钥和私钥是 “一对”,称为密钥对(key pair),且具有数学关系。和对称加密的密钥一样,非对称加密的公钥和私钥也是都可以用来加密与解密的。不过,公钥加密后只能用私钥解密,反过来,私钥加密后也只能用公钥解密,所以,非对称加密具有 “单向” 性”。
那么,非对称加密究竟是如何解决了 “密钥交换” 的问题呢?很简单:因为非对称加密具有 “单向性”,所以公钥加密后只能用私钥解密。又因为用于密钥交换的是公钥,私钥由持有者严格保密,所以黑客是拿不到私钥的,拿不到私钥就没法解密。
目前最流行的对称加密算法莫过于 AES(Advanced Encryption Standrad),中文译为 “高级加密标准”,这里不对对称加密进行叙述,主要为非对称加密,也就是标题的RSA算法。
RSA 算法,是一种使用最广泛的公钥加密算法。RSA 是由罗纳德·李维斯特(Ron Rivest)、阿迪·萨莫尔(Adi Shamir)和伦纳德·阿德曼(Leonard Adleman)在 1977 年一起提出的。RSA 就是他们三人姓氏开头字母拼在一起组成的。到目前为止,世界上还没有任何可靠的攻击 RSA 算法的方式。只要其钥匙的长度足够长,用 RSA 加密的信息实际上是不能被破解的。
RSA算法使用
Python 的 rsa 库是一个纯 Python 的 RSA 算法实现库,它支持加密、解密、数字签名、签名验证和密钥对生成。
首先需要安装rsa库,因为它不是python的标准库:
pip3 install rsa
之后我们生成密钥对:
import rsa
(pubkey, privkey) = rsa.newkeys(512)
print(pubkey)
print(privkey)
"""
PublicKey(9223201080301381374328674000891059621815405229062956973708382334740987005604653901545256508919450433111995143735691254174732723714765252437606285950020733, 65537)
PrivateKey(9223201080301381374328674000891059621815405229062956973708382334740987005604653901545256508919450433111995143735691254174732723714765252437606285950020733, 65537, 3501993311903498392034953138504556626474427326853573116464888322896908929084259958028100808527886562109109797075498537216663639460488867541344885645272833, 6513063124157132603921868352876056214111917059675276752538274908589109130267949713, 1416108043862229981660760952974644326569521678485521893757791490574602541)
"""
加密与解密
import rsa
# 1. 生成密钥对
(pubkey, privkey) = rsa.newkeys(512)
# 2. 明文信息
message1 = 'Hello world!'.encode('utf8')
print(message1)
# 3. 加密过程,由明文生成密文
crypto = rsa.encrypt(message1, pubkey)
print(crypto)
# 4. 解密过程,由密文得到明文
message2 = rsa.decrypt(crypto, privkey)
print(message2.decode('utf8'))
"""
b'Hello world!'
b'J\x16M\xa0\x04\xc0\xab#\xcc\xb4\xa0\x08\xf3)\xc4\xe9\xba\xc7\x7fe\xe6"\x05/\x00Hg\xf0\xa7R\xcb*p\x8c"Z"\n^;\xec\x86\xf5G\xa3y\x0ca\x06N/\xd6vA\xde\x87cOB\x8e\x81\\\xb9\xe5'
Hello world!
"""
根据输出结果,我们可以发现RSA完成了解密,而newkeys中的512参数为设定加密字符串的最大可支持加密长度为512位=64字节,也可设置更大,但越长加密越慢,越短越快。
另外,产生的公钥和私钥如果需要做持久化,即下一次不再生成,而是直接使用,那么需要写成文件,并使用RSA已有的api:
import rsa
(pubkey, privkey) = rsa.newkeys(512)
# 将公钥和私钥以pem编码格式保存
pub = pubkey.save_pkcs1()
pri = privkey.save_pkcs1()
# print(pub)
# print("="* 50)
#print(pri)
with open("public.pub", 'w+') as file: # public.pub,保存的文件名,可更改路径,这里保存在当前路径下
file.write(pub.decode("utf-8"))
# 将私钥保存到文件
with open("private.pem", 'w+') as file:
file.write(pri.decode('utf-8'))
# 取出公钥
with open("public.pub", "r") as file_pub:
# 从文件中读出数据
pub_data = file_pub.read()
# 将读出数据通过PublicKey.load_pkcs1()转换为公钥
pubkey = rsa.PublicKey.load_pkcs1(pub_data)
print(pubkey,"...........pubkey")
# 取出私钥
with open("private.pem", "r") as file_pri:
pri_data = file_pri.read()
# 将读出数据通过PrivateKey.load_pkcs1()转换为私钥
prikey = rsa.PrivateKey.load_pkcs1(pri_data)
print(prikey,"............prikey")
"""
PublicKey(11616142837760961663477137635683518156392668707040931592203181892182442947880343513558869734380874801838713765793389223068307986195867309166836567379275239, 65537) ...........pubkey
PrivateKey(11616142837760961663477137635683518156392668707040931592203181892182442947880343513558869734380874801838713765793389223068307986195867309166836567379275239, 65537, 7989344010438002151170056287721967451964532126430413224873863982027306949518681041551384026383775445608769844965155553725533072875424464682453292661472473, 7212438921373633362529379396709743014699633011273915843118686790038049289582827019, 1610570704916087942480896445392560437540143424340925540939237828186799381) ............prikey
"""
数字签名
数字签名(又称公钥数字签名)是只有信息的发送者才能产生的别人无法伪造的一段数字串,这段数字串同时也是对信息的发送者发送信息真实性的一个有效证明。它是一种类似写在纸上的普通的物理签名,但是使用了公钥加密领域的技术来实现的,用于鉴别数字信息的方法。
在现实世界中,我们对某一文件进行签名,代表我们认可某一事实而不能事后反悔或否认。例如我们在借条上签名,代表了我们承认我们借了钱这一事实而无法事后反悔。数字签名存在的意义与之类似,数字签名的作用可以总结如下:
- 防否认,数字信息发布者只要对发布的数字信息做了数字签名,便无法否认自己发布过这一信息;并且除了合法的签名者之外,任何其他人伪造其签名是困难的。
- 身份鉴别,数字信息接收者可以通过接收到的数字签名来鉴别发送者的身份是否正确。经签名的消息不能被篡改。一旦签名的消息被篡改,则任何人都可以发现消息与签名之间的不一致性。
根据以上内容,我们可以总结如下:
- 数字签名是需要数字信息发送者除数字信息本体外额外发送的一段数字信息;
- 信息接收者可以使用数字签名来鉴别发送者的身份及防止发送者否认发送过的信息;
- 数字签名的实现依赖于公钥加密技术。
可能从文字上来看,还是比较抽象,那么直接上图,下图依然是实验楼课件的关于生成签名和验证签名的两个过程:
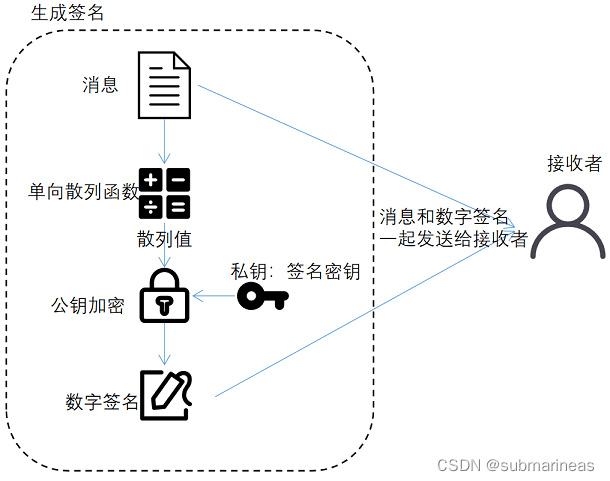
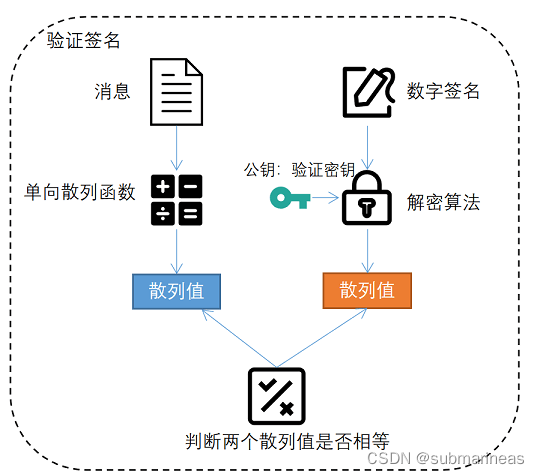
可以看到数字签名是使用签名密钥进行对该散列值进行加密生成密文,这段密文就是所谓的数字签名,但感觉这图还是不如CTF-wiki关于数字签名的图足够清晰:

RSA数字签名认证
python中使用RSA库模拟数字签名实现思路为:
- 使用 newkeys 方法生成签名密钥对:
(verifykey, signkey) = rsa.newkeys(512)
- 使用 compute_hash 方法计算消息散列值:
message = b"I like blockchain."
message_hash = rsa.compute_hash(message, 'SHA-1')
- 使用 sign_hash 生成签名:
signature = rsa.sign_hash(message_hash, signkey, 'SHA-1')
- 使用 verify 方法验证签名:
rsa.verify(message, signature, verifykey)
下面我们通过测试代码,来分别测试以下三种情况:1. 用正确的验证密钥验证数字签名的情况;2. 用正确的验证密钥验证伪装者的数字签名的情况;3. 用篡改过的信息验证数字签名的情况。
- 用正确的验证密钥验证数字签名的情况:
import rsa
# 创建签名公钥对
(verifykey, signkey) = rsa.newkeys(512)
# 计算消息的散列值
message = b"Hello world!"
message_hash = rsa.compute_hash(message, 'SHA-1')
# 生成数字签名
signature = rsa.sign_hash(message_hash, signkey, 'SHA-1')
# 验证正确的签名
ret = rsa.verify(message, signature, verifykey)
print(ret,"........ret")
"""
SHA-1 ........ret
"""
我们看到输出值和我们代码中写得加密算法一致,这就表明签名验证成功。
- 用正确的验证密钥验证伪装者的数字签名的情况:
import rsa
# 创建签名公钥对
(verifykey, signkey) = rsa.newkeys(512)
# 创建伪装者的密钥对
(fake_verifykey, fake_signkey) = rsa.newkeys(512)
# 计算消息的散列值
message = b"Hello world"
message_hash = rsa.compute_hash(message, 'SHA-1')
# 使用伪装者的签名密钥,生成数字签名
fake_signature = rsa.sign_hash(message_hash, fake_signkey, 'SHA-1')
# 使用正确的密钥,验证伪装者的签名
rsa.verify(message, fake_signature, verifykey)
我们可以看到,后台直接抛出异常,证明验证失败:
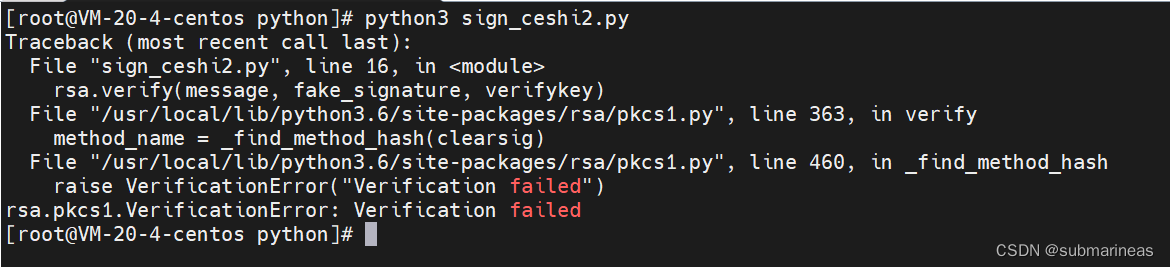
- 用篡改过的信息验证数字签名的情况:
import rsa
# 创建签名公钥对
(verifykey, signkey) = rsa.newkeys(512)
# 计算消息的散列值
message = b"Hello world"
message_hash = rsa.compute_hash(message, 'SHA-1')
# 生成数字签名
signature = rsa.sign_hash(message_hash, signkey, 'SHA-1')
# 接收者接收到的信息被篡改过,验证签名
fake_message = b"Hello World!"
rsa.verify(fake_message, signature, verifykey)
结果同样:
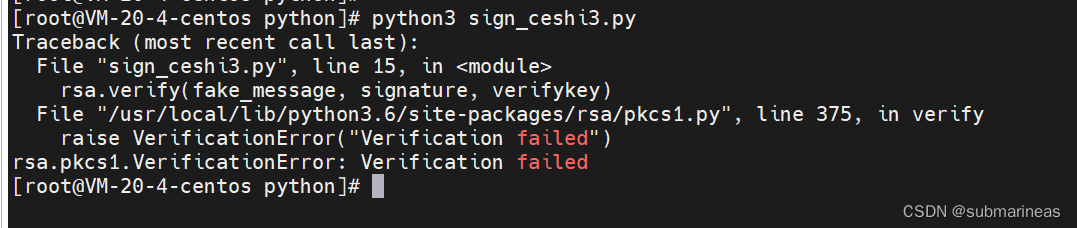
那么至此,就完成了数字签名这个概念的解释和意义,如果对于RSA还想了解得更加深入,可以去看CTF-wiki的针对RSA的2018年的两道考题,看起来是ctf靶场赛题,我之前没咋玩过,只能说以一种LeetCode的心态去看题,如下:
2018 Backdoor Awesome mix1
def PKCS1_pad(data):
asn1 = "3021300906052b0e03021a05000414"
ans = asn1 + data
n = len(ans)
return int(('00' + '01' + 'ff' * (1024 / 8 - n / 2 - 3) + '00' + ans), 16)
程序希望我们给出 n,e 使得程序满足:
h ( m ) e m o d n = p a d ( m ) h(m)^e mod \ n=pad(m) h(m)emod n=pad(m)
这里我们已经知道 h(m),pad(m)。显然如果我们控制 e=1的话,那么:
h ( m ) − p a d ( m ) = k n h(m)-pad(m)=kn h(m)−pad(m)=kn
那么如果我们可以设置 k=1,既可以得到 n。
答案为:
from Crypto.Hash import SHA
from pwn import *
from Util import PKCS1_pad
#context.log_level = 'debug'
def main():
port = 12345
host = "127.0.0.1"
p = remote(host, port)
p.recvuntil('Message -> ')
message = p.recvuntil('\n\nSignature -> ', drop=True)
log.info('message: ' + message)
signature = p.recvuntil('\n', drop=True)
log.info('signature: ' + signature)
h = SHA.new(message)
m = PKCS1_pad(h.hexdigest())
e = 1
n = int(signature, 16) - m
p.sendlineafter('Enter n:', str(n))
p.sendlineafter('Enter e:', str(e))
p.interactive()
main()
程序输出:
➜ 2018-BackdoorCTF-Awesome-mix1 git:(master) python exp.py
[+] Opening connection to 127.0.0.1 on port 12345: Done
[*] message: super important information for admin only
[*] signature: 721af5bd401b5f2aff8e86bf811b827cdb5877ef12202f24fa914a26f235523f80c45fdbf0d3c9fa77278828ddd8ca0551a941bd57c97dd38654692568d1357a49e7a2a284d296508602ead24c91e5aa7f517b9e48422575f0dd373d00f267a206ba164ab104c488268b5f95daf490a048407773d4b1016de8ef508bf1aa678f
[*] Switching to interactive mode
CTF{cryp70_5ur3_15_w13rd}
[*] Got EOF while reading in interactive
搞ctf的可以去靶场下找到2018年当前题的一个环境去验证结果,以及还有同年的另一道RSA题,为2018 Backdoor Awesome mix2,这里我就不再尝试了,那么至此,本篇结束。
参考与推荐
[1]. https://www.lanqiao.cn/courses/3056
[2]. https://stackoverflow.com/questions/9594125/salt-and-hash-a-password-in-python?noredirect=1&lq=1
[3]. 密码学系列之:bcrypt加密算法详解
[4]. CTF Wiki