一、什么是RC吸收?
RC吸收是指在电路设计中,尤其是在开关电源、功率电子设备以及电力电子系统中,使用电阻与电容串联组成的电路结构,用于吸收和衰减电路中由于开关元件(如MOSFET、IGBT等)的快速切换所产生的过电压和过电流现象。
反激变换器在 MOS 关断的瞬间,由变压器漏感 LLK与 MOS 管的输出电容造成的谐振尖峰加在 MOS 管的漏极,如果不加以限制,MOS 管的寿命将会大打折扣。 因此需要采取措施,把这个尖峰吸收掉
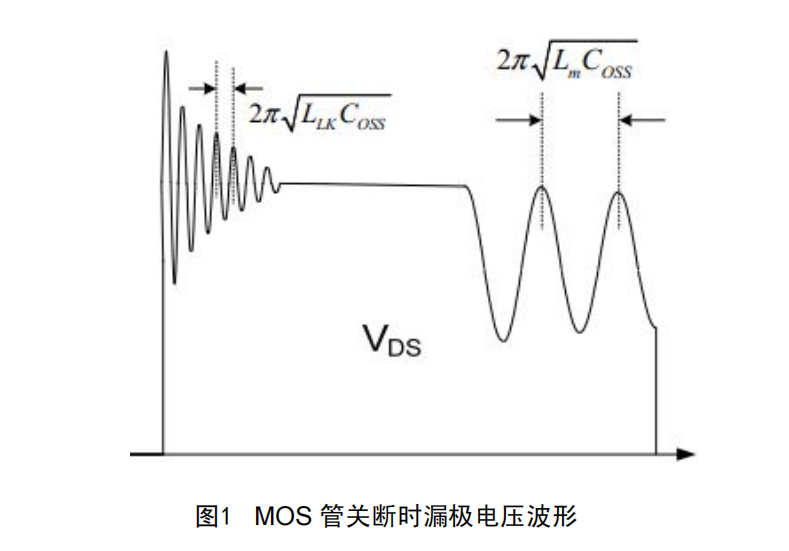
吸收是针对电压尖峰而言,电压尖峰从何而来?电压尖峰的本质是什么?
电压尖峰的本质是一个对结电容的dv/dt充放电过程,而dv/dt是由电感电流的瞬变(di/dt)引起的,所以,降低di/dt或者dv/dt的任何措施都可以降低电压尖峰,这就是吸收。
二、RC吸收的作用是什么?
1、降低尖峰电压。
2、缓冲尖峰电流。
3、降低di/dt和dv/dt,即改善EMI品质。
4、减低开关损耗,即实现某种程度的软开关。
5、提高效率。提高效率是相对而言的,若取值不合理不但不能提高效率,弄不好还可能降低效率。
三、RC吸收的特点
1、双向吸收。一个典型的被吸收电压波形中包括上升沿、上升沿过冲、下降沿这三部分,RC吸收回路在这三各过程中都会产生吸收功率。通常情况下我们只希望对上升沿过冲实施吸收。因此这意味着RC吸收效率不高。
2、不能完全吸收。这并不是说RC吸收不能完全吸收掉上升沿过冲,只是说这样做付出的代价太大。RC吸收最好定一个合适的吸收指标,不要指望它能够把尖峰完全吸收掉。
3、RC吸收是能量的单向转移,就地将吸收的能量转变为热能。尽管如此,这并不能说损耗增加了,在很多情况下,吸收电阻的发热增加了,与电路中另外某个器件的发热减少是相对应的,总效率不一定下降。设计得当的RC吸收,在降低电压尖峰的同时也有可能提高效率。
四、吸收的误区
1、Buck续流二极管反压尖峰超标,就拼命的在二极管两端加RC吸收。 这个方法却是错误的。为什么?因为这个反压尖峰并不是二极管引起的,尽管表现是在这里。这时只要加强MOS管的吸收或者采取其他适当的措施,这个尖峰就会消失或者削弱。
2、副边二极管反压尖峰超标,就在这个二极管上拼命吸收。 这种方法也是错误的,原因很清楚,副边二极管反压尖峰超标都是漏感惹的祸,正确的方法是处理漏感能量。
3、反激MOS反压超标,就在MOS上拼命吸收。这种方法也是错误的。如果是漏感尖峰,或许吸收能够解决问题。如果是反射电压引起的,吸收不但不能能够解决问题的,效率还会低得一塌糊涂,因为你改变了拓扑。
五、吸收的改善
书上网络上都有关于吸收回路的计算方法的介绍,但由于寄生参数的影响,这些公式几乎没有实际意义,实际上大部分的RC参数是靠实验来调整的,但RC的组合理论上有无穷多,怎么来初选这个值是很关键的,下面来介绍一些实用的理论和方法:
1、先不加RC,用容抗比较低的电压探头测出原始的震荡频率(注意用低电容的探头,因为探头的电容会引起震铃频率的改变,使设计结果不准),此震荡是有LC 形成的,LC主要是变压器次级漏感和布线的电感和输出电容,C主要是二极管结电容和变压器次级的杂散电容。

测量二极管D两端原始振荡频率。此设计中为33.3MHz(未加RC吸收前):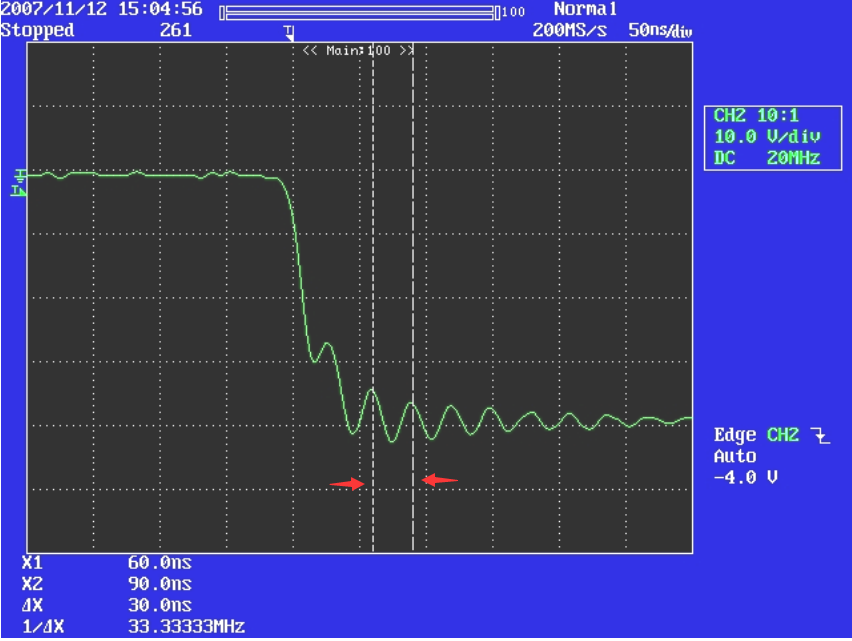
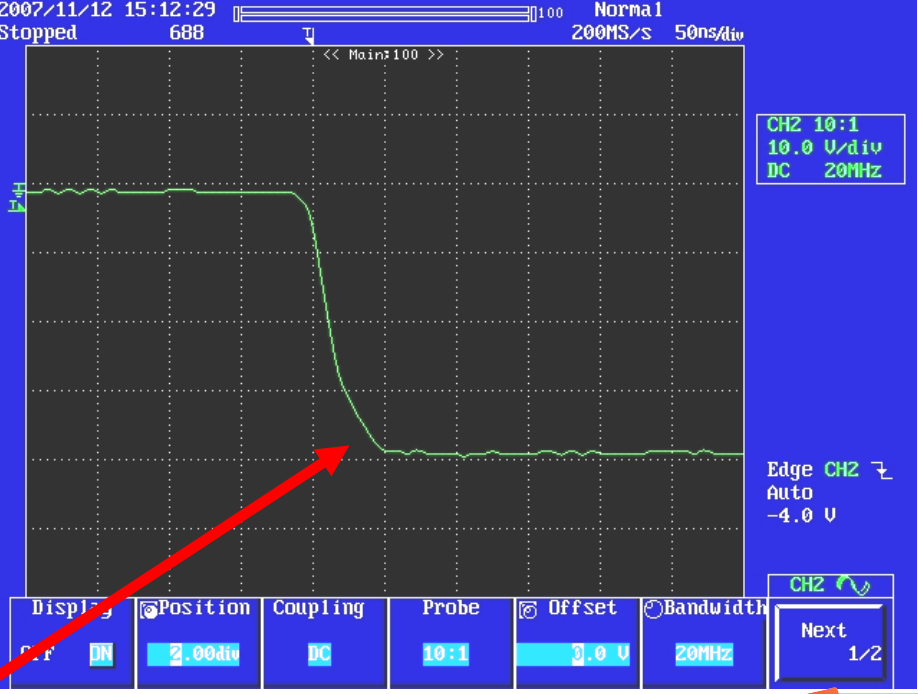
2、测出原始震荡频率后,可以试着在二极管上面加电容(与二极管并联方式),直到震荡频率变为原来的1/2(一半),如图增加的电容为470pF,下图的震荡频率变为16.7MHz(只加了C9后):

则原来震荡的C(杂散电容)为所加电容的1/3(意思是470pF=3*C),震荡的主体由原来的C变为了我们所加的电容C9;

3、知道了吸收电容C9的值就可以算R值了:
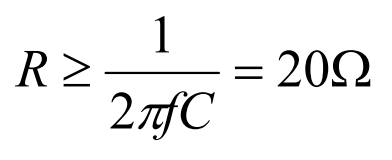
一般把R加到吸收C上时,震荡就可以大大衰减。这时再适当调整C值的大小,直到震荡基本被抑制。
六、吸收电路测试经验总结
1、吸收电容C的影响
1、并非吸收越多损耗越大,适当的吸收有一个效率最高点。
2、吸收电容C的大小与吸收功率(R的损耗)呈正比关系。即:吸收功率基本上由吸收电容决定。
2、吸收电阻R的影响
1、吸收电阻的阻值对吸收效果干系重大,影响明显。
2、吸收电阻的阻值对吸收功率影响不大,即:吸收功率主要由吸收电容决定。
3、当吸收电容确定后,一个适中的吸收电阻才能达到最好的吸收效果。
4、当吸收电容确定后,最好的吸收效果发生在发生最大吸收功率处。换言之,哪个电阻发热最厉害就最合适。
5、当吸收电容确定后,吸收程度对效率的影响可以忽略。