我们以下述代码为例来说明函数调用堆栈的详细过程
#include<iostream>
int sum(int a,int b)
{
int temp=0;
temp=a+b;
return temp;
}
int main()
{
int a=10;
int b=20;
int ret=sum(a,b);
std::cout<<"ret:"<<ret<<std::endl;
return 0;
}接下来,我们逐行分析代码的执行
为局部变量分配空间
首先,当代码执行到main函数后,会为main函数开辟栈帧空间,需要说明的是
- 栈这个数据结构需要两个指针来维护,分别是栈底指针和栈顶指针
- 在x86结构里,负责存放栈底指针的寄存器是ebp,负责存放栈顶指针的寄存器是esp
- 栈空间是向下增长的,故内存地址随着栈帧的开辟会减小
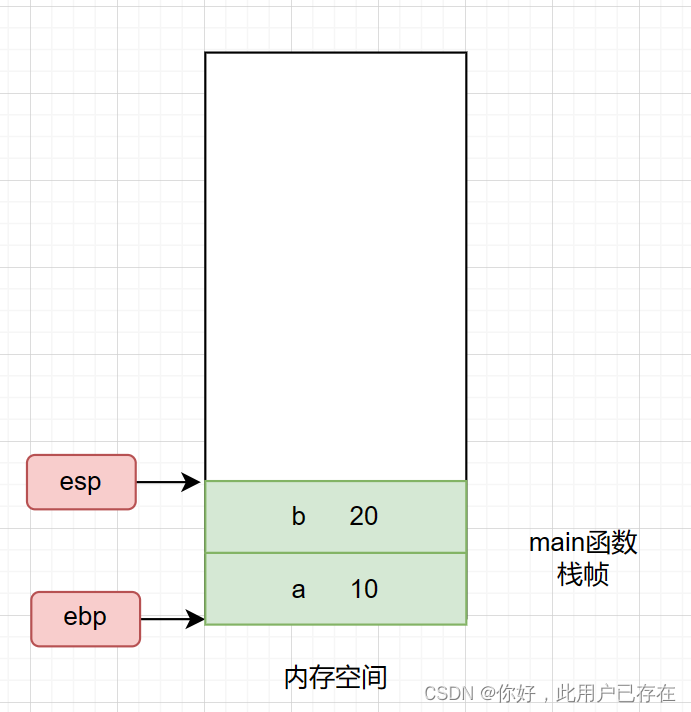
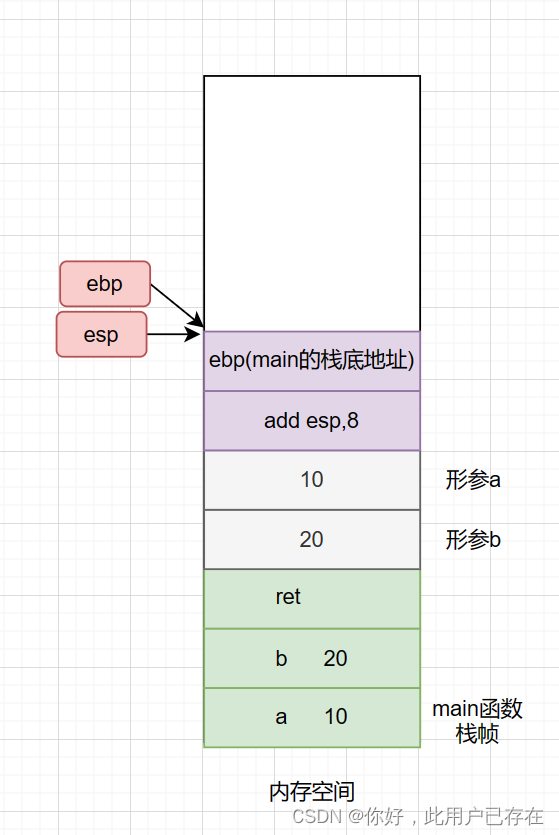
如下所示,刚开始时,系统在内存中为main开辟的栈帧空间
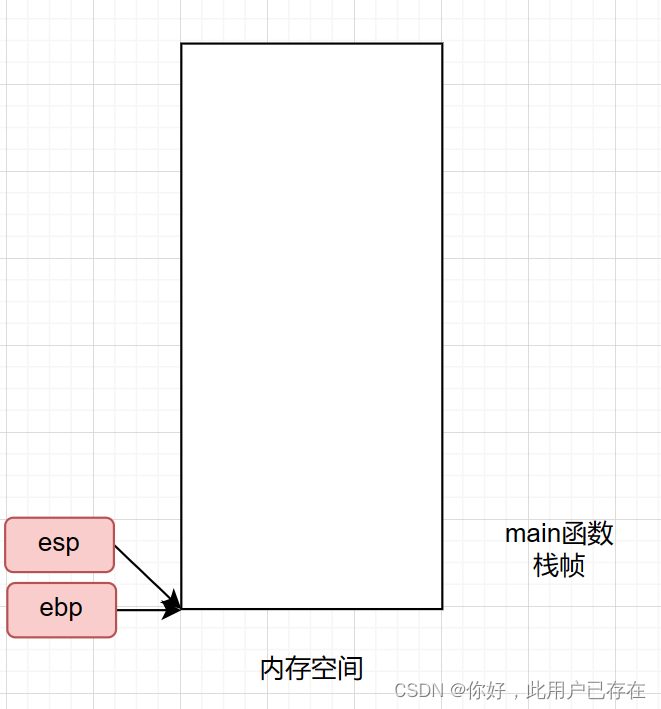
当执行到以下代码时,系统会为变量a和变量b开辟栈帧,同时对其进行初始化
int a=10;
int b=20;汇编指令为
mov dword ptr[ebp-4],0Ah
mov dword ptr[ebp-8],14h其中,int a=10;这段代码对应的汇编指令解释如下
- dword ptr,表示操作一个双字(也就是四个字节)的数据
- [ebp-4],表示以
ebp寄存器为基址,偏移-4个字节的内存地址。因为栈是向下生长的,所以-4表示当前栈帧中的一个局部变量或者其他数据存储位置,通常是相对于栈顶的位置。- 0Ah,十进制数字10的十六进制表示
- mov,移动指令
故这段代码中表示,将值10存储到当前函数栈帧存储位置的前 4 个字节中。
此时,内存空间的栈帧情况如下所示
函数调用
准备工作
接下来,当执行到这段代码时,系统会做以下几件事情
int ret=sum(a,b);
- 为局部变量ret开辟栈帧空间
- 为形参变量a和b开辟栈帧空间
- 调用sum函数
1.为局部变量ret开辟栈帧
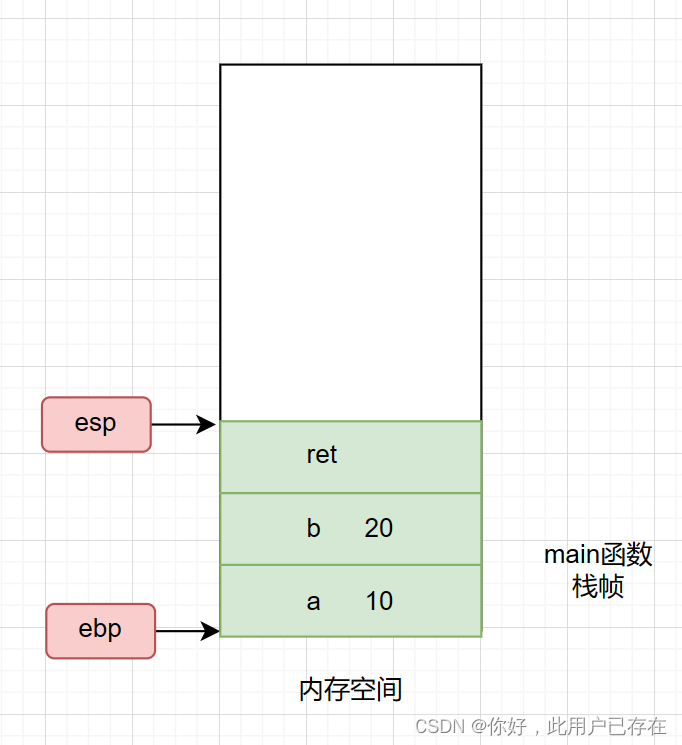
2.为形参变量开辟栈帧
需要说明的是,在为形参变量开辟栈帧空间时,是从右往左进行开辟的,也就是说是先开辟形参b的空间再开辟形参a的空间
压入形参b的汇编指令为
mov eax,dword ptr[ebp-8];从内存中取出变量b(内存地址为ebp-8)的数据,放到寄存器eax中
push eax;将取出的形参b的数据压入栈中同理,压入形参a的汇编指令为
mov eax,dword[ebp-4]
push eax此时内存空间的状态为
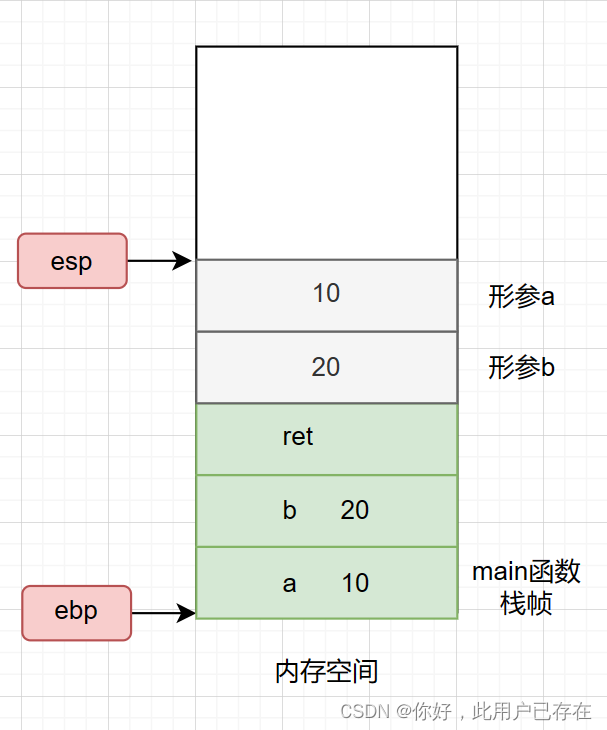
3.调用函数sum
该过程会使用汇编指令call调用函数sum,而在进入函数sum内部之前,call指令会进行一些准备工作
- 保存下一条指令的地址,也就是将下一条指令的地址压入栈中
- 保存函数调用前的上下文环境
(1)首先将下一条指令的地址压入栈中
由于系统为形参变量分配了内存空间,而当函数调用结束后会回收这块内存空间,因此下一条指令就是回收函数形参变量内存空间的指令,如下所示,就是将栈顶指针esp“增加四个字节的偏移”(栈是向下增长的,开辟栈空间是esp减去偏移,回收栈空间时esp增加偏移)
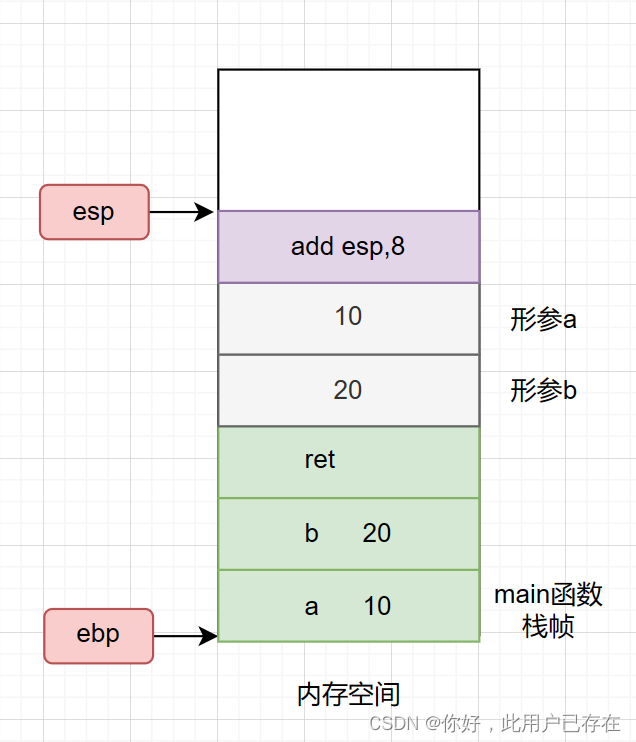
(2)保存上下文环境
在这里所谓的保存上下文环境,就是保存main函数栈帧空间的ebp值(栈的栈底地址)
因为进入sum函数后,会为sum函数开辟单独的栈空间,因此ebp值会被覆盖,而为了要在sum函数调用结束后回到main函数的栈空间,就需要将此时的ebp值进行保存,如下所示
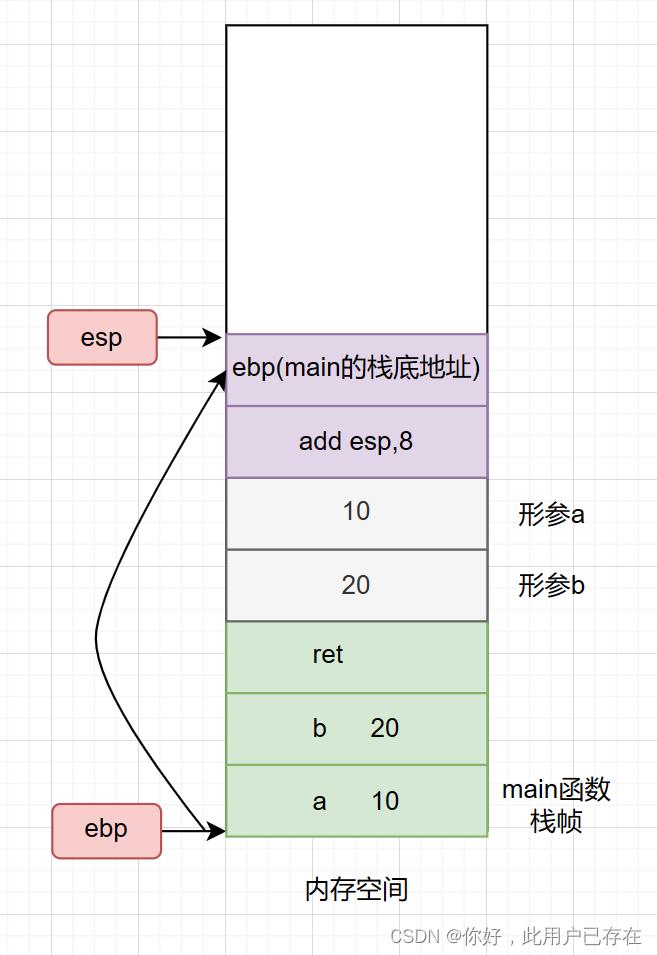
之后,将ebp(栈低地址)移动到esp的位置,并移动esp(栈顶指针)为sum函数开辟栈帧空间,如下所示
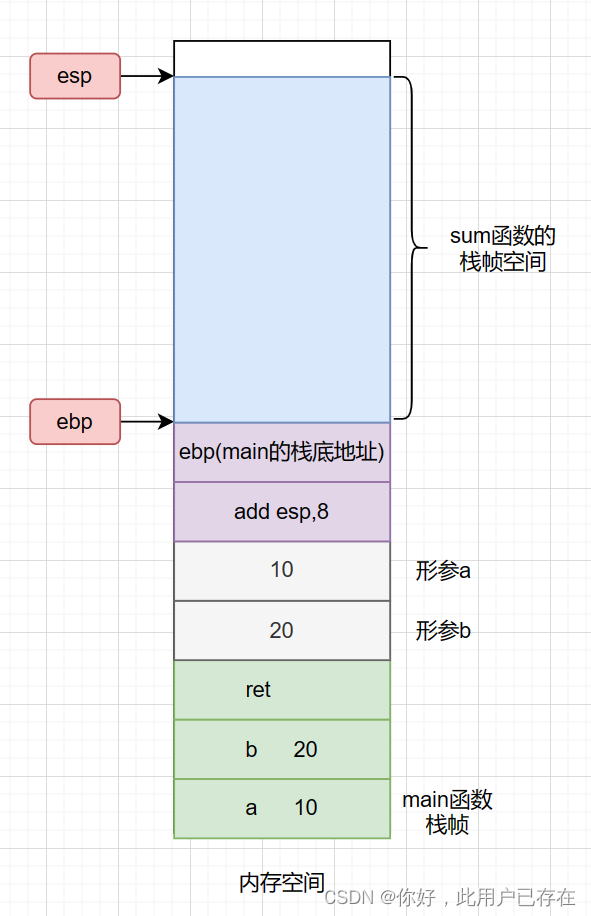
该过程的汇编过程为
push ebp
mov ebp,esp
sub esp,4Ch值得说明的是,该过程也就是sum函数的大括号里左括号 { 的作用
进入函数内部
当系统为sum函数开辟完栈帧空间之后,就已经进入sum函数内部了,接下来就在sum函数这个栈帧空间里执行sum函数的代码
int temp=0;首先,上述这段代码的汇编指令为
mov dword ptr[ebp-4],0如下所示,内存空间的状态为
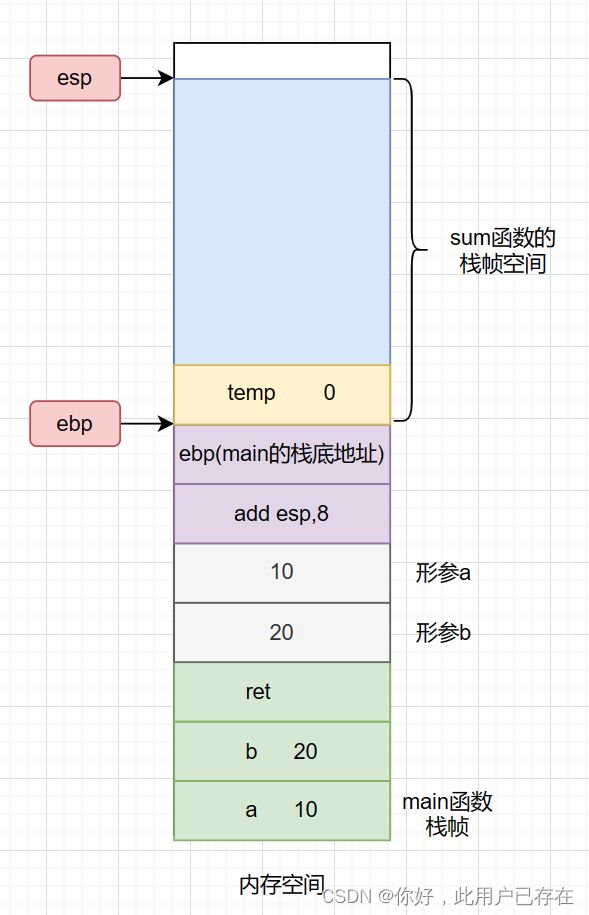
temp=a+b;同理,这段代码的汇编过程为
mov eax,dword ptr[ebp+0Ch];取出形参a的值,放入到寄存器eax中
add eax,dword ptr[ebp+8];取出形参b的值,并与形参a的值(在寄存器eax)相加,并将相加后的结果放到eax中
mov dword ptr[ebp-4],eax;将运算结果赋值为temp此时,内存空间的状态为
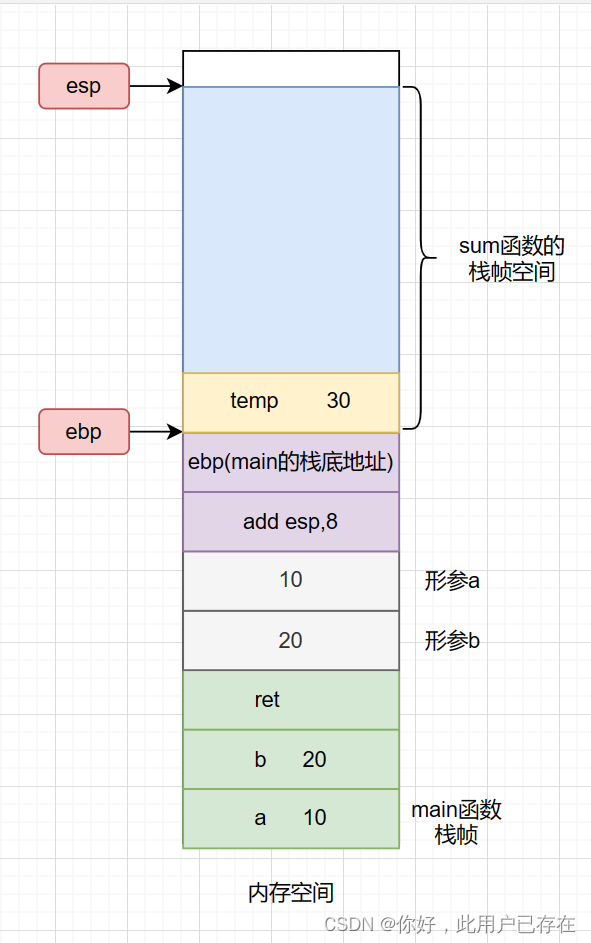
接下来,执行这段代码
return temp;该过程为函数返回,这段代码的汇编结果是将temp的值保存到寄存器eax中,即
mov eax,dword ptr[ebp-4]接下来,就要开始回收栈帧空间
栈帧空间回收
1.首先,直接回退栈顶指针esp到ebp,汇编指令为
mov esp,ebp此时内存空间的状态为
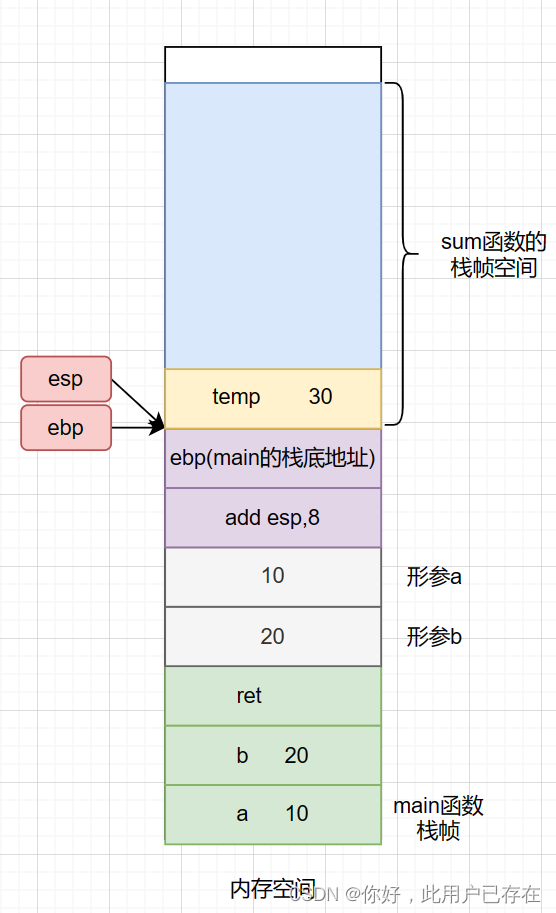
需要说明的是,该过程并没有清空sum函数栈帧空间的内容,也就是说,此时仍旧可以访问到函数内部的局部变量的值,但是如果在sum函数回退之后还有其他函数的执行,则必然会重新开辟栈帧空间,此时就会把sum函数的局部变量的值给覆盖掉
这也是为什么不建议返回一个局部指针和局部引用的原因,因为指针和引用类型的局部变量并不是按值返回的,也就是说返回时并不进行拷贝,这样就会很可能就会访问一个非法空间
2.接下来,系统会弹出栈顶值,而从图中可以看到,此时栈顶指针esp指向的值是进入sum函数前保存的main的栈底地址,因此,该过程会让ebp重新回退到main的栈底
该过程的汇编指令为
pop ebp此时,内存空间的状态为
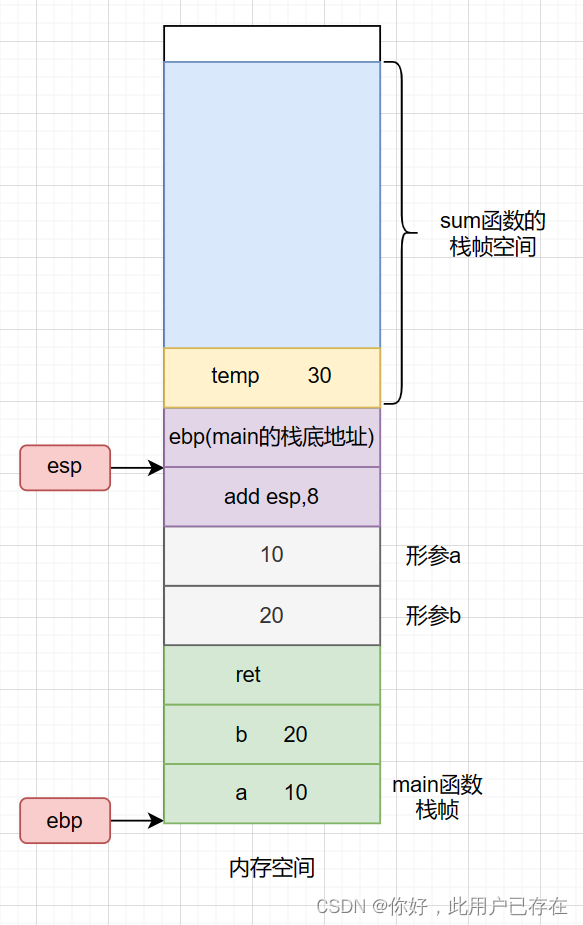
需要说明的是,该过程也就是sum函数代码里右括号 } 的作用,即
mov esp,ebp pop ebp
3.接下来,系统会调用ret指令
ret指令的作用是将此时栈顶指针的内容赋值为IP寄存器,由图我们知道,此时栈顶指针esp保存的是进入sum函数前下一条指令的地址,而IP寄存器的作用就是指向下一条需要执行的指令的地址
此时状态为

由图我们可以看到,上述指令的执行结果是回收main函数分配的形参变量空间,因此执行结束后,内存空间的状态为
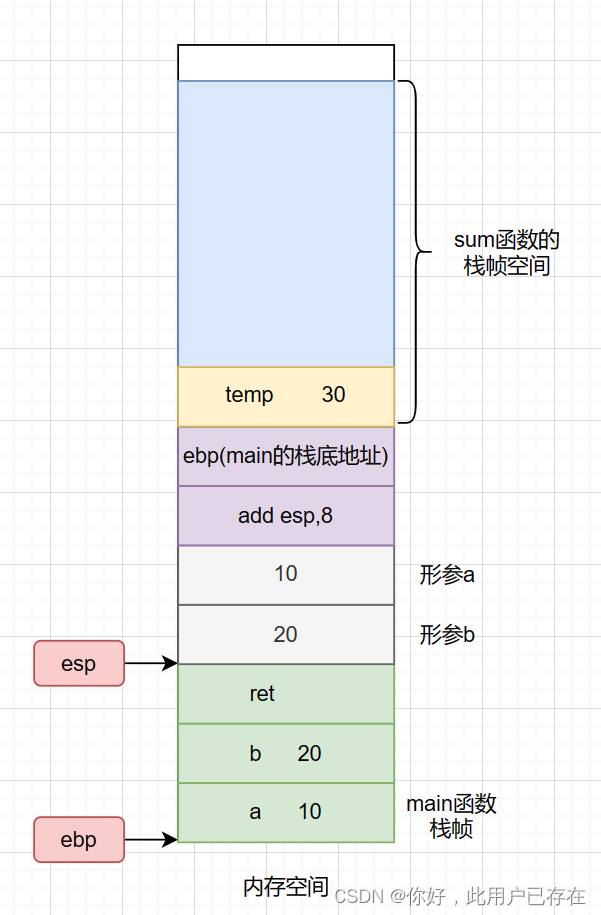
至此,sum函数的栈帧空间就已经退出了
接下来,系统会执行以下指令,将函数的执行结果(此前返回时保存在寄存器eax中)返回给ret
mov dword ptr[ebp-0Ch],eax即
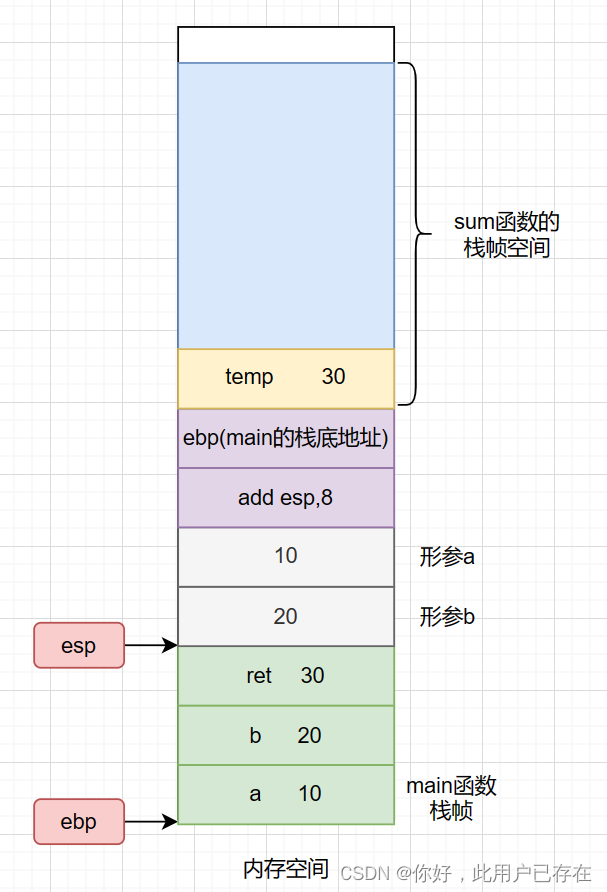
至此,整个的函数调用的堆栈过程就结束了