感谢西工大严老师的无私奉献!!
低成本MEMS INS系统 + GNSS组合导航MATLAB仿真
- 感谢西工大严老师的无私奉献!!
- 一、kalman参数初始化——kfinit()
- 二、imu添加误差——imusdderr()
- 三、imu位姿更新——insupdate()
- 四、kalman误差方程——kfft15()
- 五、kalman滤波——kfupdate()
- 六、主程序:
- 七、仿真结果
- 八、程序及数据下载地址
一、kalman参数初始化——kfinit()

%________________________________________________________________________
% 输入:
% Qk: 系统的状态噪声,15*15的对角矩阵,Qk = diag([web; wdb; zeros(9,1)])^2*nts;
% Rk: 系统的测量噪声,6*6的对角矩阵,rk = [[0.1;0.1;0.1];[[10;10]/Re;10]]; Rk = diag(rk)^2;
% P0: 初始状态的协方差矩阵,15*15的对角矩阵,P0 = diag([delta_a;delta_v;delta_p;delta_eb;delta_db])^2;
% Phikk_1: 状态转移矩阵
% Hk: 量测转移矩阵
% Gammak: 状态噪声驱动矩阵
% 输出:
% kf:
%_________________________________________________________________________
function kf = kfinit(Qk, Rk, P0, Phikk_1, Hk, Gammak)
[kf.m, kf.n] = size(Hk); % kf.m:量测维数; kf.n:状态维数
kf.Qk = Qk; kf.Rk = Rk; % 状态噪声和量测噪声
kf.Pk = P0; kf.Xk = zeros(kf.n,1); % 初始状态和初始状态误差协方差矩阵
kf.Phikk_1 = Phikk_1; kf.Hk = Hk; % 状态转移矩阵和量测矩阵
if nargin<6, kf.Gammak = eye(kf.n); % 状态噪声驱动矩阵
else kf.Gammak = Gammak; end
二、imu添加误差——imusdderr()
function [wm, vm] = imuadderr(wm, vm, eb, web, db, wdb, ts) % IMU添加零偏与游走误差
m = size(wm,1); sts = sqrt(ts);
wm = wm + [ ts*eb(1) + sts*web(1)*randn(m,1), ...
ts*eb(2) + sts*web(2)*randn(m,1), ...
ts*eb(3) + sts*web(3)*randn(m,1) ];
vm = vm + [ ts*db(1) + sts*wdb(1)*randn(m,1), ...
ts*db(2) + sts*wdb(2)*randn(m,1), ...
ts*db(3) + sts*wdb(3)*randn(m,1) ];
三、imu位姿更新——insupdate()
具体编写过程请参考我的其他两篇博客:
1、高、低成本MEMS惯导系统姿态、位置、速度更新算法的对比
2、低成本MEMS惯导系统的捷联惯导解算MATLAB仿真
function [qnb,vn2,pos,eth]=insupdate(qnb,vn1,pos,delta_theta_m,delta_v_m,ts)
nn=1; %子样数
nts=nn*ts;
g0=9.780325333434361; %单位;m/s^2
sl = sin(pos(1)); % pos(1)=L
sl2 = sl*sl; sl4 = sl2*sl2;
gLh = g0*(1+5.27094e-3*sl2+2.32718e-5*sl4)-3.086e-6*pos(3);
gn = [0;0;-gLh];
eth = earth(pos, vn1); % 地球相关参数计算
%速度更新
vsf =q2mat(qnb)*(delta_v_m + 1/2*cross(delta_theta_m,delta_v_m))';
vn2 = vn1 + vsf + gn*nts;
%位置更新
vn1 = (vn2+vn1)/2;
pos = pos + [vn1(2)/eth.RMh;vn1(1)/eth.clRNh;vn1(3)]*nts;
%姿态更新
q_bb = [cos(norm(delta_theta_m)/2);(delta_theta_m/norm(delta_theta_m))'*sin((norm(delta_theta_m)/2))];
qnb = qmul(rv2q(-eth.wnin*nts), qmul(qnb, q_bb)); % 姿态更新
qnb = qnormlz(qnb);
end
四、kalman误差方程——kfft15()




function Ft = kfft15(eth, Cnb, fb)
global g0 ff
tl = eth.tl; secl = 1/eth.cl; L = eth.pos(1); h = eth.pos(3);
f_RMh = 1/eth.RMh; f_RNh = 1/eth.RNh; f_clRNh = 1/eth.clRNh;
f_RMh2 = f_RMh*f_RMh; f_RNh2 = f_RNh*f_RNh;
vE_clRNh = eth.vn(1)*f_clRNh; vE_RNh2 = eth.vn(1)*f_RNh2; vN_RMh2 = eth.vn(2)*f_RMh2;
Mp1 = [ 0, 0, 0; % 4.2.33a
-eth.wnie(3), 0, 0;
eth.wnie(2), 0, 0 ];
Mp2 = [ 0, 0, vN_RMh2;
0, 0, -vE_RNh2;
vE_clRNh*secl, 0, -vE_RNh2*tl]; % 4.2.33c
beta = 5.27094e-3; beta1 = (2*beta+ff)*ff/8; beta2 = 3.086e-6; beta3 = 8.08e-9;
Mp3 = [0,0,0; -2*beta3*h,0,-beta3*sin(2*L); -g0*(beta-4*beta1*cos(2*L))*sin(2*L),0,beta2]; % 对M3的补偿项
Maa = askew(-eth.wnin); % 4.2.38_1
Mav = [ 0, -f_RMh, 0;
f_RNh, 0, 0;
f_RNh*tl, 0, 0 ]; % 4.2-33b
Map = Mp1+Mp2; % 4.2.38_2
Mva = askew(Cnb*fb);
Mvv = askew(eth.vn)*Mav - askew(eth.wnien); % 4.2.40 1-3
Mvp = askew(eth.vn)*(Mp1+Map)+Mp3;
Mpv = [ 0, f_RMh, 0;
f_clRNh, 0, 0;
0, 0, 1 ]; % 4.2.42a
Mpp = [ 0, 0, -vN_RMh2;
vE_clRNh*tl, 0, -vE_RNh2*secl;
0, 0, 0 ]; % 4.2.42b
O33 = zeros(3);
%% phi dvn dpos eb db
Ft = [ Maa Mav Map -Cnb O33
Mva Mvv Mvp O33 Cnb
O33 Mpv Mpp O33 O33
zeros(6,15) ];
五、kalman滤波——kfupdate()


Kalman滤波过程可用流程框图表示:

function kf = kfupdate(kf, Zk, TimeMeasBoth) % T: 进行时间更新,M: 进行量测更新,B: 进行时间更新和量测更新
% **************************************************************
%名称:Kalman filter update
% 输入:
% kf: k-1时刻的kalman filter参数
% Zk: k时刻传感器测得的量测信息
% time_measure_both:
% 输出:
% kf: k时刻的kalman filter参数
% **************************************************************
if nargin==1, TimeMeasBoth = 'T'; % 如果没有量测输入,则只进行时间更新
elseif nargin==2, TimeMeasBoth = 'B'; end % 有量测输入,进行时间更新和量测更新
if TimeMeasBoth=='T' || TimeMeasBoth=='B' % 时间更新
kf.Xkk_1 = kf.Phikk_1*kf.Xk;
kf.Pkk_1 = kf.Phikk_1*kf.Pk*kf.Phikk_1' + kf.Gammak*kf.Qk*kf.Gammak';
else % TimeMeasBoth=='M'
kf.Xkk_1 = kf.Xk;
kf.Pkk_1 = kf.Pk;
end
if TimeMeasBoth=='M' || TimeMeasBoth=='B' % 量测更新
kf.PXZkk_1 = kf.Pkk_1*kf.Hk';
kf.PZkk_1 = kf.Hk*kf.PXZkk_1 + kf.Rk;
kf.Kk = kf.PXZkk_1/kf.PZkk_1;
kf.Xk = kf.Xkk_1 + kf.Kk*(Zk-kf.Hk*kf.Xkk_1);
kf.Pk = kf.Pkk_1 - kf.Kk*kf.PZkk_1*kf.Kk';
else % TimeMeasBoth=='T'
kf.Xk = kf.Xkk_1;
kf.Pk = kf.Pkk_1;
end
kf.Pk = (kf.Pk+kf.Pk')/2; % P阵对称化
六、主程序:
clc
clear
gvar;
imu=load ('imu.mat'); % imu数据: avp=[wm, vm, tt(2:end)]; gx(rad) gy gz ax (m/s) ay az time
trj=load ('trj.mat'); % trj=[att, vn, pos]; att(度) vn(米每秒) pos(米)
arcdeg = pi/180;
nn=1; % 子样数
ts=0.01; % 单个采样间隔的采样时间长度
nts=nn*ts; % 采样周期,在nts时间内进行两次采样,每次采样 0.1秒
%初始化参数
att = [0;0;90]*arcdeg; vn0 = [0;0;0]; pos0 = [[34;108]*arcdeg;100]; % att -- 欧拉角;arcdeg -- 度转换为弧度;vn -- 速度;pos -- 位置
qnb0 = a2qua(att);
qnb = qnb0; vn = vn0; pos = pos0; % 姿态、速度和位置初始化
%添加误差
phi = [0.1; 0.2; 3]*arcmin; qnb = qaddphi(qnb, phi); % 失准角
eb = [0.01;0.015;0.02]*dph; web = [0.001;0.001;0.001]*dpsh; % 陀螺常值零偏,角度随机游走
db = [80;90;100]*ug; wdb = [1;1;1]*ugpsHz; % 加速度计常值偏值,速度随机游走
% ug=ge*1e-6; g0 = ge; ge -- 赤道重力; ugpsHz= ug/sqrt(1);
%初始化kalman参数
Qk = diag([web; wdb; zeros(9,1)])^2*nts; % Qk系统噪声
rk = [[0.1;0.1;0.1];[[10;10]/Re;10]]; Rk = diag(rk)^2; % Rk量测噪声
P0 = diag([[0.1;0.1;10]*arcdeg; [1;1;1]; [[10;10]/Re;10]; % Re赤道长半轴
[0.1;0.1;0.1]*dph; [80;90;100]*ug])^2; % 协方差矩阵,x = [phi, delta_vn, delta_p, eb, db]
Hk = [zeros(6,3),eye(6),zeros(6)];
kf = kfinit(Qk, Rk, P0, zeros(15), Hk);
len=length(imu.avp);
avps=zeros(fix(len/2),10);
avps(1,:)=[att;vn;pos;0]';
t=0;kk=1;err = zeros(len, 10); xkpk = zeros(len, 2*kf.n+1);
for k=1:nn:len
t=t+nts;
delta_theta_m=imu.avp(k,1:3);
delta_v_m=imu.avp(k,4:6);
[wm_b, vm_b] = imuadderr(delta_theta_m, delta_v_m, eb, web, db, wdb, ts);% IMU添加零偏与游走误差
[qnb,vn,pos,eth]=insupdate(qnb,vn,pos,wm_b,vm_b,ts);
kf.Phikk_1 = eye(15) + kfft15(eth, q2mat(qnb), sum(vm_b,1)'/nts)*nts; % kf.Phikk_1 = Phikk_1; kfft15 -- SINS误差转移矩阵
kf = kfupdate(kf); % Kalman滤波时间更新
if mod(t,0.01)<nts
gps = trj.trj(k,4:9)' + rk.*randn(6,1); % GPS速度位置仿真
kf = kfupdate(kf, [vn;pos]-gps, 'M'); % Kalman滤波量测更新
end
%误差反馈
qnb = qdelphi(qnb,kf.Xk(1:3)); kf.Xk(1:3) = 0; % kf.Xk = zeros(kf.n,1); qdelphi -- 四元数真实值=四元数计算值-失准角;误差反馈
vn = vn - kf.Xk(4:6); kf.Xk(4:6) = 0; %每次减完都需要把当前时刻的估计误差给扣除,也就是最后把姿态、速度、位置误差全部清零。
pos = pos - kf.Xk(7:9); kf.Xk(7:9) = 0;
err(kk,:) = [qq2phi(qnb,a2qua(trj.trj(k,1:3))'); vn-trj.trj(k,4:6)';
pos-trj.trj(k,7:9)'; t]'; % qq2phi -- 失准角误差=四元数计算值-四元数真值
xkpk(kk,:) = [kf.Xk; diag(kf.Pk); t]; % kf.Pk = P0; [kf.Xk; diag(kf.Pk); t] -- 反馈后的剩余状态、方差阵和时间
kk=kk+1;
cnb=q2att(qnb);
cnb(3)=mod(cnb(3),2*pi); % avp()=[θ γ ψ VE VN VU B L h t]
avps(kk,:)=[cnb; vn; pos; t]';
if mod(t,1)<nts, disp(fix(t));
end % 显示进度 disp函数:显示文本或数组
end
%姿态
tt=length(avps);
tf=length(trj.trj);
figure(1);
subplot(321);
plot(1:tt,(avps(1:tt,1:2)/arcdeg),1:tf,(trj.trj(1:tf,1:2)/arcdeg),'--'); title('俯仰角和横滚角');xlabel('d');ylabel('\theta,\gamma(\circ)');
legend('\it\theta','\it\gamma','\bf\theta','\bf\gamma');grid on;
subplot(322);
plot(1:tt,(avps(1:tt,3)/arcdeg),1:tf,(trj.trj(1:tf,3)/arcdeg),'--'); title('偏航角');xlabel('d');ylabel('\Phi(\circ)');
legend('\it\Phi','\bf\Phi') ;grid on;
subplot(323);
plot(1:tt,(avps(1:tt,4:5)),1:tf,(trj.trj(1:tf,4:5)),'--'); title('速度');xlabel('d');ylabel('Vel/(m.s^{-1})');
legend('\itv\rm_E','\itv\rm_N','\bfv\rm_E','\bfv\rm_N');grid on;
subplot(324);
plot(1:tt,(avps(1:tt,6)),1:tf,(trj.trj(1:tf,6)),'--'); title('速度');xlabel('d');ylabel('Vel/(m.s^{-1})');
legend('\itv\rm_U','\bfv\rm_U');grid on;
subplot(325);
plot(1:tt,deltapos(avps(1:tt,7:9)),1:tf,deltapos(trj.trj(1:tf,7:9)),'--'); title('位置');xlabel('d');ylabel('\DeltaPos / m');
legend('\Delta\itL', '\Delta\it\lambda', '\Delta\ith','\Delta\bfL', '\Delta\bf\lambda', '\Delta\bfh');grid on;
err(kk:end,:) = []; xkpk(kk:end,:) = []; tt = err(:,end);
% 状态真值与估计效果对比图
msplot(321, tt, err(:,1:2)/arcmin, '\it\phi\rm / ( \prime )'); % 俯仰角,滚转角误差
legend('\it\phi\rm_E', '\it\phi\rm_N') ; title('俯仰角和横滚角真值与估计值之差'); % 添加图例
msplot(322, tt, err(:,3)/arcmin, '\it\phi\rm_U\rm / ( \prime )'); title('偏航角真值与估计值之差'); % 偏航角误差
msplot(323, tt, err(:,4:6), '\delta\itv^n\rm / ( m.s^{-1} )'); title('三轴速度真值与估计值之差'); % 三轴速度误差
legend('\delta\itv\rm_E', '\delta\itv\rm_N', '\delta\itv\rm_U')
msplot(324, tt, [err(:,7)*Re,err(:,8)*Re*cos(pos(1)),err(:,9)], '\delta\itp\rm / m');title('三轴位置真值与估计值之差'); % 三轴位置误差
legend('\delta\itL', '\delta\it\lambda', '\delta\ith')
msplot(325, tt, xkpk(:,10:12)/dph, '\it\epsilon\rm / ( (\circ).h^{-1} )');title('三轴陀螺仪常值误差'); % 三轴陀螺仪常值误差
legend('\it\epsilon_x','\it\epsilon_y','\it\epsilon_z')
msplot(326, tt, xkpk(:,13:15)/ug, '\it\nabla\rm / \mu\itg'); % 三轴加速度计误差
legend('\it\nabla_x','\it\nabla_y','\it\nabla_z');title('三轴加速度计常值零偏误差');
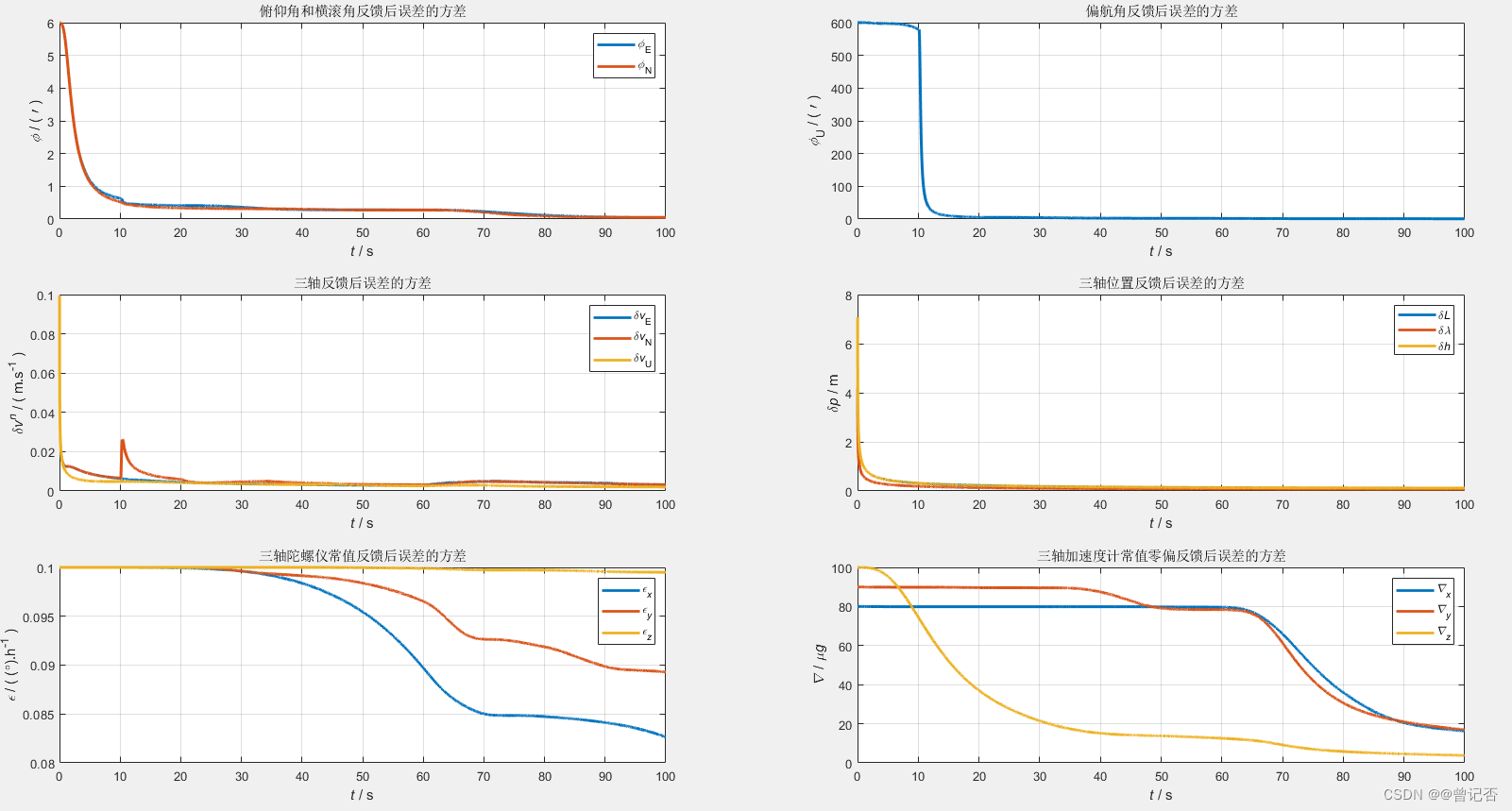
% 均方差收敛图 滤波器的可观测性
spk = sqrt(xkpk(:,16:end-1));
msplot(321, tt, spk(:,1:2)/arcmin, '\it\phi\rm / ( \prime )');title('俯仰角和横滚角反馈后误差的方差');
legend('\it\phi\rm_E', '\it\phi\rm_N'),
msplot(322, tt, spk(:,3)/arcmin, '\it\phi\rm_U\rm / ( \prime )');title('偏航角反馈后误差的方差');
msplot(323, tt, spk(:,4:6), '\delta\itv^n\rm / ( m.s^{-1} )');title('三轴反馈后误差的方差');
legend('\delta\itv\rm_E', '\delta\itv\rm_N', '\delta\itv\rm_U')
msplot(324, tt, [[spk(:,7),spk(:,8)*pos(1)]*Re,spk(:,9)], '\delta\itp\rm / m');title('三轴位置反馈后误差的方差');
legend('\delta\itL', '\delta\it\lambda', '\delta\ith')
msplot(325, tt, spk(:,10:12)/dph, '\it\epsilon\rm / ( (\circ).h^{-1} )');title('三轴陀螺仪常值反馈后误差的方差');
legend('\it\epsilon_x','\it\epsilon_y','\it\epsilon_z')
msplot(326, tt, spk(:,13:15)/ug, '\it\nabla\rm / \mu\itg');title('三轴加速度计常值零偏反馈后误差的方差');
legend('\it\nabla_x','\it\nabla_y','\it\nabla_z')
七、仿真结果


八、程序及数据下载地址
sins + gnss 组合导航算法Matlab仿真