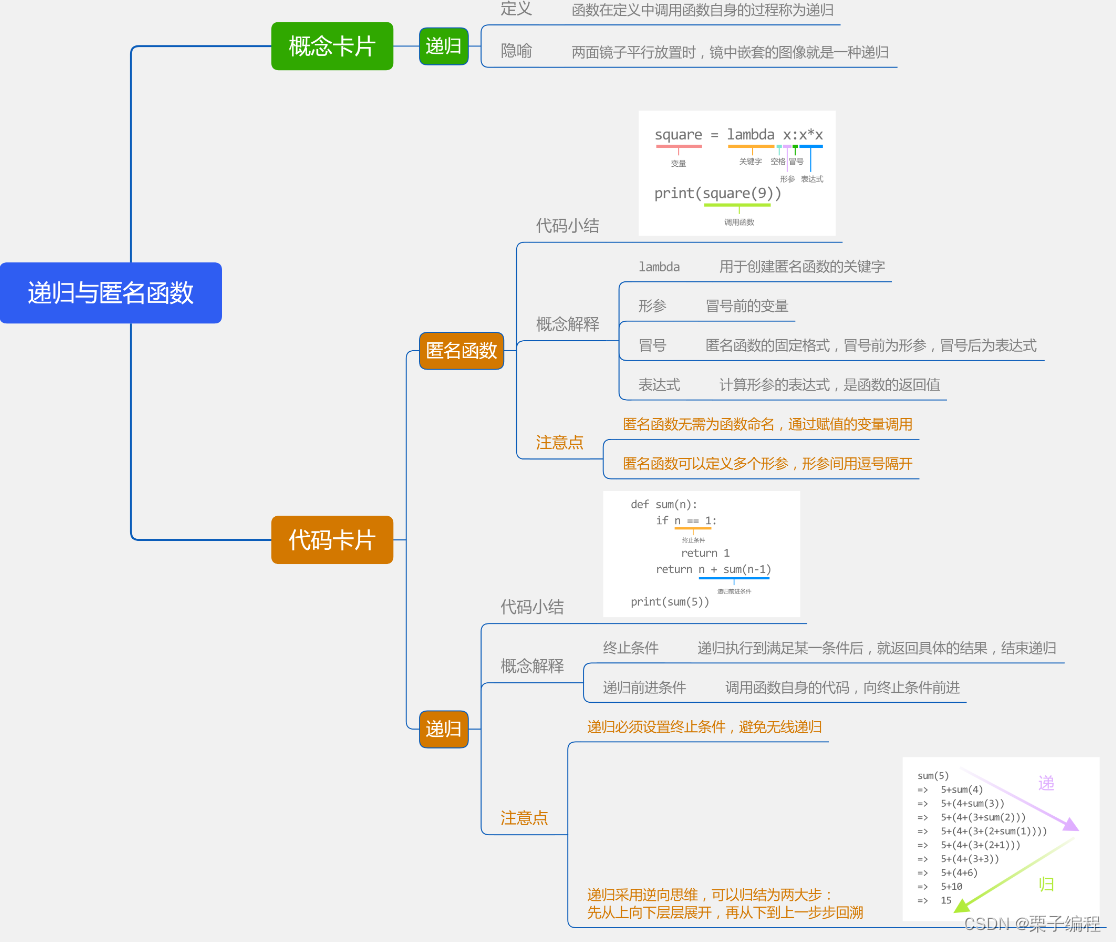
目录
目标
匿名函数
多个形参
匿名函数的局限性
递归
语言例子
数学例子
递归的实现
递归代码
练习
总结
目标
在之前的博客中,我们学习了定义函数、调用函数以及设置函数的参数。在今天,我们会补充函数的两个常见的知识点,一个是匿名函数,另一个是递归函数。下面我们先来看看什么是匿名函数吧~
匿名函数
在前面,我们使用def 函数名(参数): 的结构来定义一个函数。如果,我们把def定义的函数看作“有名字函数”。那么还有一类函数,无需定义函数名,即匿名函数。

下面这段代码创建了一个匿名函数,并赋值给了变量square。然后通过变量名square调用函数,输出了结果。
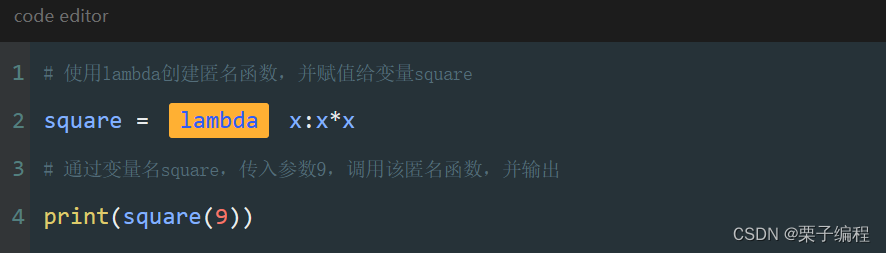
# 使用lambda创建匿名函数,并赋值给变量square
square = lambda x:x*x
# 通过变量名square,传入参数9,调用该匿名函数,并输出
print(square(9))
lambda
一个关键字lambda,用来创建匿名函数。
空格
一个空格,是创建匿名函数的固定格式。关键字lambda和后面的式子间要有一个空格。
形参
这个位置是匿名函数的参数,也就是我们前面学习的形参,用于接收实参传递来的数据。
冒号:
一个冒号:,是匿名函数的固定格式。冒号前面是形参,冒号后面是进行计算的表达式。
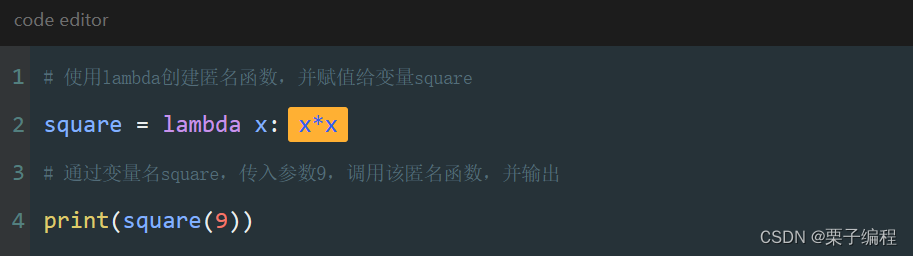
表达式
一个计算形参的表达式,紧跟在冒号后面。这个表达式,就是函数的返回值。也就是说,这个表达式的结果将返回到调用函数的地方。所以,匿名函数可以看作return型函数的简便写法。
变量
将匿名函数的值赋给变量,后续,能通过该变量来调用匿名函数。

调用函数
只要将匿名函数赋值给了变量,就需要通过对应的变量名来调用函数。示例中,通过变量square来调用该匿名函数,在括号()中传入了实参9。

多个形参
当然,匿名函数还可以设置多个形参,形参之间以逗号分隔。实例中,冒号前设置了两个形参x和y,在进行函数调用时,还是采取位置形参的方式依次传递数据。

匿名函数的局限性
匿名函数使用起来比较方便,但是它也有局限性。一般只能用来改写包含了return的简单函数。示例中,是匿名函数和普通函数的等价写法。

递归
无论是前面的自定义函数,还是匿名函数, 都是先定义好,然后函数外调用这个函数。其实,函数在自己的内部还可以调用自己,我们把这种函数称为递归函数。
下面,我们通过几个例子来熟悉一下递归的概念。

定义:通常,我们在函数定义中调用函数自身的过程叫做递归。
隐喻:两面镜子平行放置时,镜子一层一层嵌套自己就是一种递归。

语言例子
其实,有这样一个通俗的故事最能体现递归:从前有座山,山里有座庙,庙里有个老和尚,正在给小和尚讲故事呢!故事是什么呢?“从前有座山,山里有座庙,庙里有个老和尚,正在给小和尚讲故事呢!故事是什么呢?……
这里的“故事”嵌套的“故事”,就是“故事”本身。除非讲故事的人自己停下来不讲了,不然这个故事可以“无限”讲下去。

数学例子
现在,我们假设sum(n)等于前n个正整数的和,即:sum(n)=1+2+3+……+(n-1)+n。如果直接计算sum(n),我们可能会从小到大一个数一个数接连相加,1加2再加3……,依次类推。
那么使用递归的思想,又该如何解决呢?
递归的核心思想,就是大事化小,即将原始问题拆解为等价的子问题。换句话说,我们要计算sum(n),不妨先去计算更简单的sum(n-1)。但是,由于n变成了n-1,范围变小,为了保证等价,可以用sum(n-1)加上n。

同样的道理,我们要计算sum(n-1),又可以先去计算sum(n-2)。以此类推,一直计算到最简单的sum(1)=1为止。

递归的实现
如图,我们展示了计算sum(5)的递归过程。首先把sum(5)变成5+sum(4);同理,把sum(4),变成4+sum(3);……以此类推,一直到最简单的sum(1)。然后,我们就能倒推结果。由于知道sum(1),就知道了sum(2),然后可知sum(3)、sum(4)和sum(5)。

递归代码
简单学习了递归的概念和函数原理后。下面,我们将以计算5以内正整数的累加和为例,来学习递归代码。

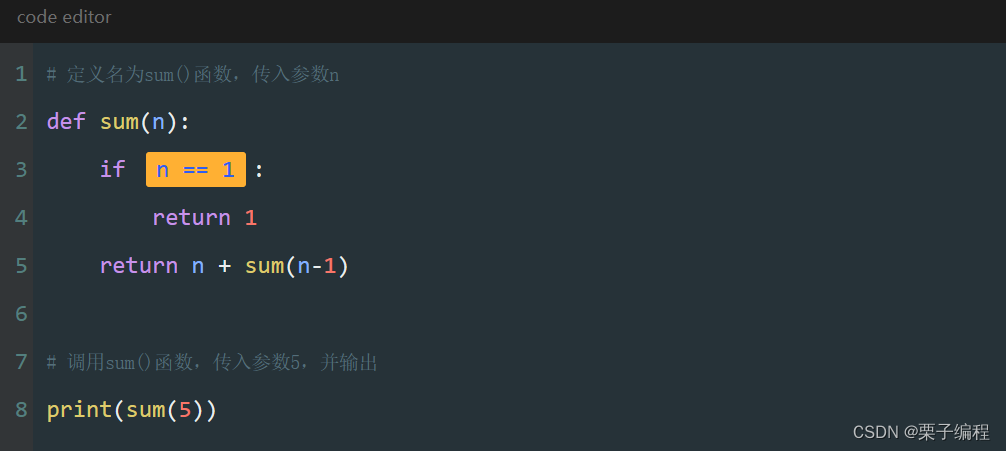
这段函数定义一个求和函数sum,并通过递归的方式求得了5以内的数字的累加和。
# 定义名为sum()函数,传入参数n
def sum(n):
if n == 1:
return 1
return n + sum(n-1)
# 调用sum()函数,传入参数5,并输出
print(sum(5))
终止条件
终止条件,是递归执行到满足某一条件后,就返回具体的结果,避免程序无限递归下去。因为,要计算5以内的正整数之和,而最小的正整数为1。所以,示例中n的值为1时,就会将1返回到调用函数处。
递归前进条件
递归的前进条件,表示函数调用自身的代码,通常是和原函数等价的表达式。通过前面的例子,我们知道sum(n)等于n加上sum(n-1)。所以,函数返回了n+sum(n-1)。

练习
200以内求和
定义一个递归函数,用于计算实现 200 以内的正整数之和。将函数名命名为 sum,传入参数为 n。
参考代码
# 定义sum()函数,传入参数n
def sum(n):
if n==1:
return 1
return n+sum(n-1)
# 调用sum()函数,传入200,并输出
print(sum(200))
总结