面试专题课:
北大硕士LeetCode算法专题课--递归和回溯_骨灰级收藏家的博客-CSDN博客
北大硕士LeetCode算法专题课-栈、队列相关问题_骨灰级收藏家的博客-CSDN博客
北大硕士LeetCode算法专题课--链表相关问题_骨灰级收藏家的博客-CSDN博客
北大硕士LeetCode算法专题课-查找相关问题_骨灰级收藏家的博客-CSDN博客
北大硕士LeetCode算法专题课-字符串相关问题_骨灰级收藏家的博客-CSDN博客
北大硕士LeetCode算法专题课-数组相关问题_骨灰级收藏家的博客-CSDN博客
北大硕士LeetCode算法专题课-基础算法查找_骨灰级收藏家的博客-CSDN博客
北大硕士LeetCode算法专题课-基础算法之排序_骨灰级收藏家的博客-CSDN博客
北大硕士LeetCode算法专题课---算法复杂度介绍_骨灰级收藏家的博客-CSDN博客
什么是动态规划
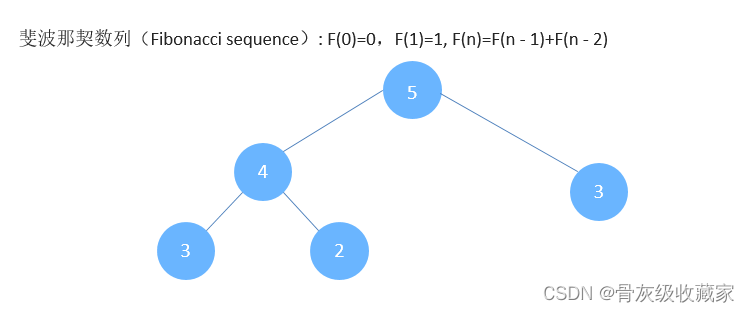
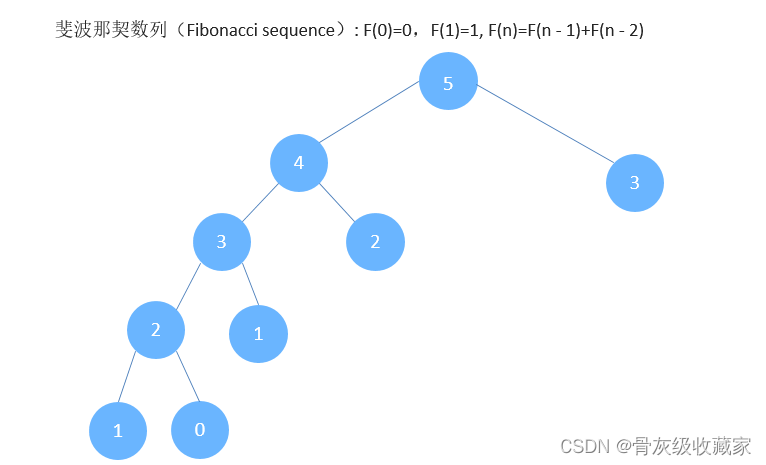
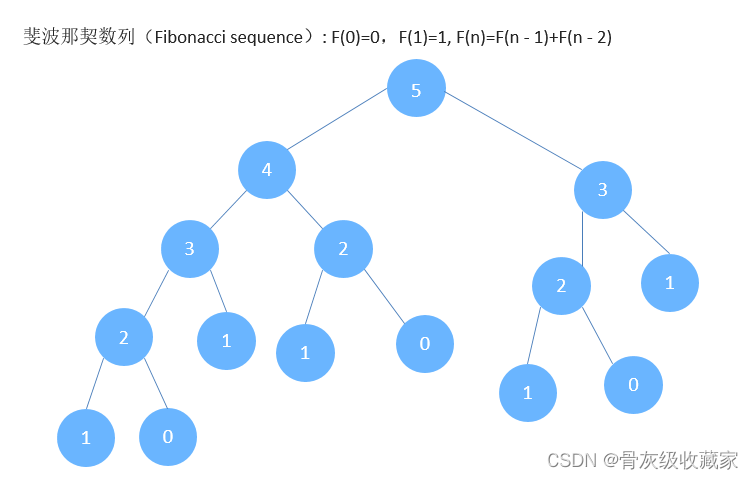
我们以斐波那契数列为例来说明什么是动态规划
斐波那契数列(Fibonacci sequence): F(0)=0,F(1)=1, F(n)=F(n - 1)+F(n - 2)
import time
def fib(n):
if n == 0:
return 0
if n == 1:
return 1
return fib(n - 1) + fib(n - 2)
if name == ' main ': t1 = time.time()
n = fib(10)
t2 = time.time()
print("n = %d, 用时%d 毫秒" % (n, (t2 - t1) * 1000))
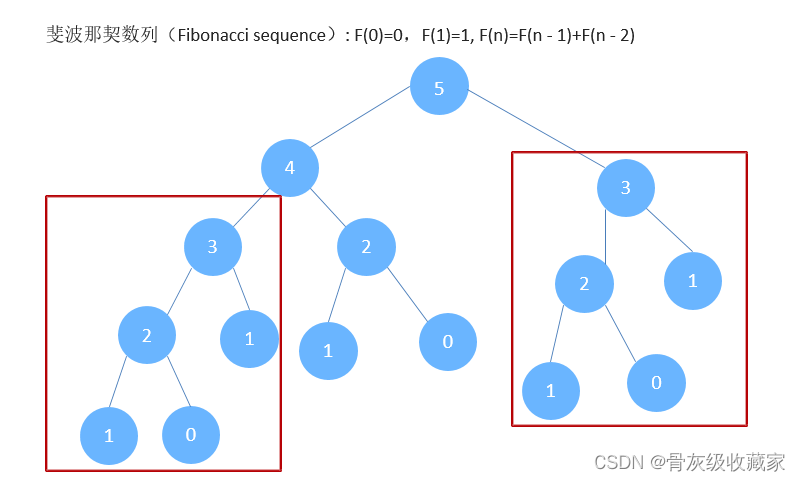
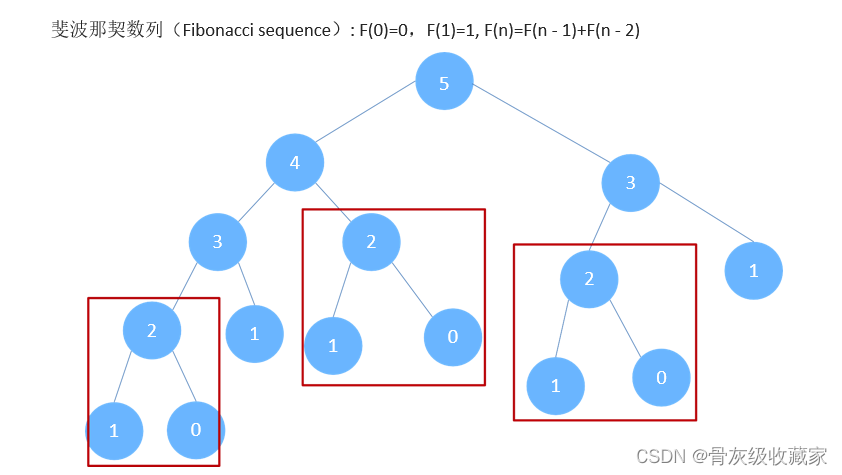
斐波那契数列,优化: 记忆化搜索
def fib2(n):
global num num += 1 if n == 0:
return 0
if n == 1:
return 1
if res[n] == -1:
res[n] = fib2(n - 1) + fib2(n - 2)
return res[n]
if name == ' main ':
res = [-1 for i in range(41)] t1 = time.time()
n = fib2(40)
t2 = time.time()
print("n = %d, 用时%d 毫秒,执行了%d次" % (n, (t2 - t1) * 1000, num))
记忆化搜索:自上向下的解决问题
def fib2(n):
global num num += 1 if n == 0:
return 0
if n == 1:
return 1
if res[n] == -1:
res[n] = fib2(n - 1) + fib2(n - 2)
return res[n]
动态规划:把大问题拆分成小问题,通过寻找大问题与小问题的递推关系,解决一个个小问题,在解决小问题的时候, 记忆每一个小问题的答案,使得每个小问题只解决一次,最终达到解决原问题的效果。
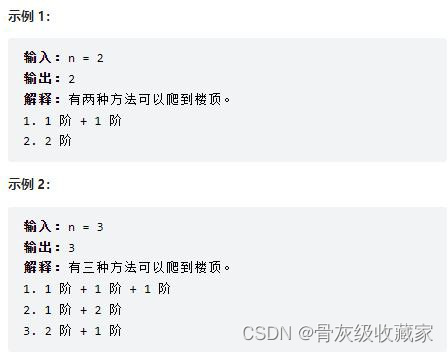
 爬楼梯 (LeetCode 70)
爬楼梯 (LeetCode 70)
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?提示:1 <= n <= 45
解题思路:假设f(n) 表示爬 n 阶楼梯可能的走法。
自顶向下的思路: 假设当前站在第n阶楼梯上,那么上一步可能在第n-1 或者 n-2 阶, 分别需要爬1级台阶和2级台阶 所以 f(n) = f(n-1) + f(n-2)
代码实现1 暴力搜索 上面式子中 n-2>=0 所以 最后一次递归调用为 f(2) = f(1) + f(0),边界就是 f(1) = 1,f(0) = 1
def climbStairs(n):
if n == 0 or n == 1:
return 1
return climbStairs(n - 1) + climbStairs(n - 2)
代码实现2 记忆化搜索
def climbStairs2(n): def dfs(i, memo):
if i == 0 or i == 1:
return 1
if memo[i] == -1:
memo[i] = dfs(i - 1, memo) + dfs(i - 2, memo)
return memo[i]
return dfs(n, [-1] * (n + 1))
代码实现3 动态规划
def climbStairs3(n): res = [0] * (n + 1) res[0] = res[1] = 1
for i in range(2, n + 1):
res[i] = res[i - 1] + res[i - 2]
return res[-1]
整数拆分 (LeetCode 343)
假设给定一个正整数 n ,将其拆分为 k 个 正整数 的和( k >= 2 ),并使这些整数的乘积最大化。 返回 你可以获得的最大乘积 。2 <= n <= 58

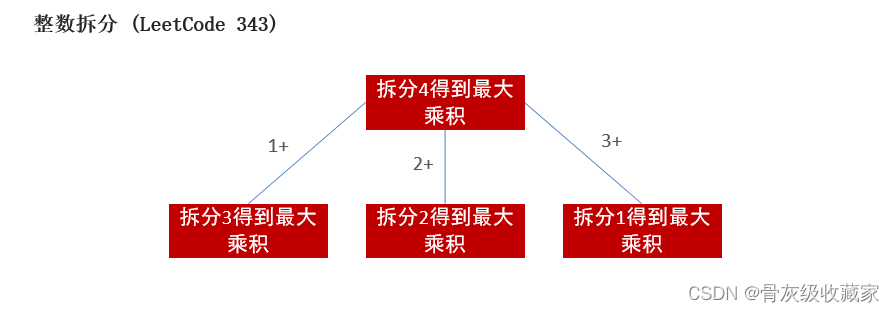
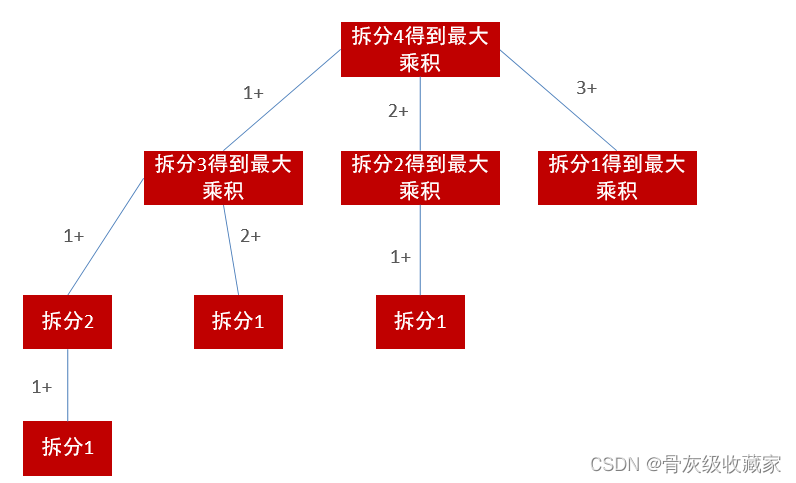
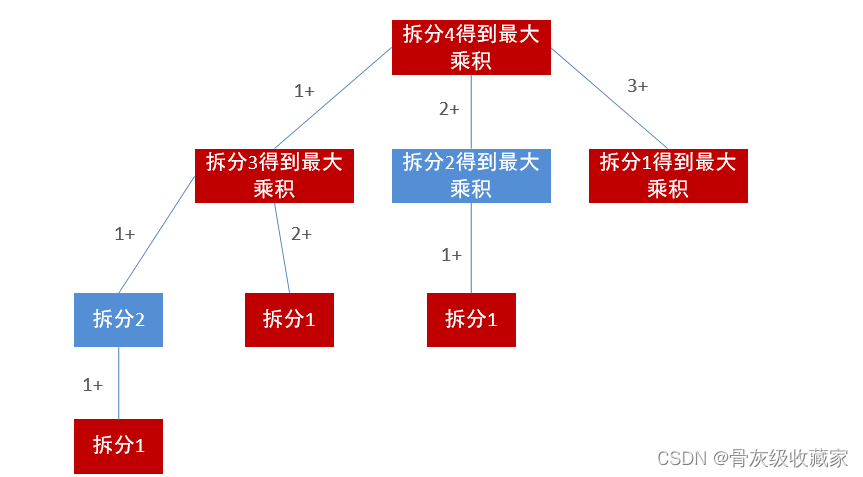
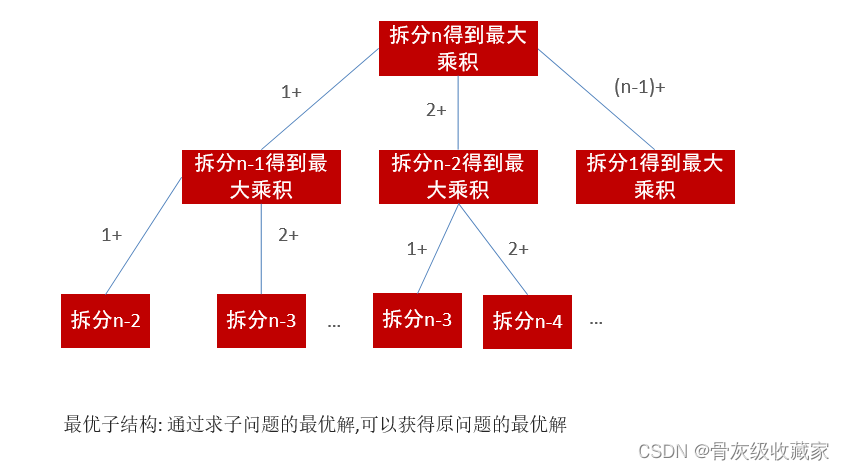
def integerBreak(n): def dfs(n, memo):
if n ==1:
return 1
if memo[n] !=-1: return memo[n]
res = -1
for i in range(1,n):
res = max(res,i*(n-i),i*dfs(n-i,memo)) memo[n] = res
return res
return dfs(n,[-1] * (n + 1))
def integerBreak(n): dp = [0] * (n + 1)
for i in range(2, n + 1):
for j in range(i):
dp[i] = max(dp[i], j * (i - j), j * dp[i - j])
return dp[n]
打家劫舍 (LeetCode 198)
你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是 相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
定一个代表每个房屋存放金额的非负整数数组,计算你 不触动警报装置的情况下 ,一夜之内能够偷窃到的最高金额。
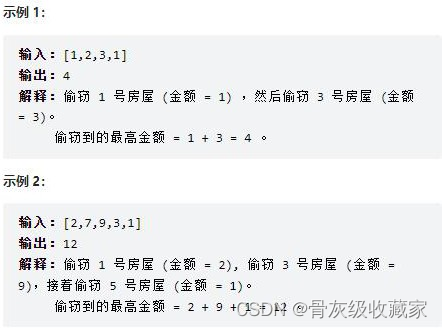
先考虑最简单的情况。如只有一间房屋,则偷窃该房屋,可以偷到最高总金额。如只有两间房屋,则由于两间房屋相邻, 不能同时偷窃,只能偷窃其中的一间房屋,因此选择其中金额较高的房屋进行偷窃,可以偷窃到最高总金额。
如果房屋数量大于两间,应该如何计算能够偷窃到的最高总金额呢?
对于第 k (k>2) 间房屋,有两个选项:
l 偷窃第 k 间房屋,那么就不能偷窃第 k-1 间房屋,偷窃总金额为前 k-2 间房屋的最高总金额与第 k 间房屋的金额之和。
l 不偷窃第 k 间房屋,偷窃总金额为前 k-1 间房屋的最高总金额。
在两个选项中选择偷窃总金额较大的选项,该选项对应的偷窃总金额即为前 k 间房屋能偷窃到的最高总金额。 用 dp[i] 表示前 i 间房屋能偷窃到的最高总金额,那么就有如下的状态转移方程:

def rob(nums): if not nums:
return 0
size = len(nums)
if size == 1:
return nums[0]
dp = [0] * size dp[0] = nums[0]
dp[1] = max(nums[0], nums[1])
for i in range(2, size):
dp[i] = max(dp[i - 2] + nums[i], dp[i - 1])
return dp[size - 1]
发饼干 (LeetCode 455)
假设你是一位很棒的家长,想要给你的孩子们一些小饼干。但是,每个孩子最多只能给一块饼干。
对每个孩子 i,都有一个胃口值 g[i],这是能让孩子们满足胃口的饼干的最小尺寸;并且每块饼干 j,都有一个尺寸 s[j] 。 如果 s[j] >= g[i],我们可以将这个饼干 j 分配给孩子 i ,这个孩子会得到满足。
你的目标是尽可能满足越多数量的孩子,并输出这个最大数值。

贪心算法(又称贪婪算法)是指,在对问题求解时,总是做出在当前看来是最好的选择,就能得到问题的答案。贪心 算法需要充分挖掘题目中条件,没有固定的模式,解决有贪心算法需要一定的直觉和经验。
为了尽可能满足最多数量的孩子,从贪心的角度考虑,应该按照孩子的胃口从小到大的顺序依次满足每个孩子,且 对于每个孩子,应该选择可以满足这个孩子的胃口且尺寸最小的饼干。
首先对数组 g 和 s 排序,然后从小到大遍历 g 中的每个元素,对于每个元素找到能满足该元素的 s 中的最小的元素。 具体而言,令 i 是 g 的下标,j是 s 的下标,初始时 i 和 j 都为 0,进行如下操作。
对于每个元素 g[i],找到未被使用的最小的 j 使得 g[i]≤s[j],则 s[j] 可以满足 g[i]。由于 g 和 s 已经排好序,因此整个过 程只需要对数组 g 和 s 各遍历一次。当两个数组之一遍历结束时,说明所有的孩子都被分配到了饼干,或者所有的 饼干都已经被分配或被尝试分配(可能有些饼干无法分配给任何孩子),此时被分配到饼干的孩子数量即为可以满 足的最多数量。
def findContentChildren(g, s): g.sort()
s.sort()
n, m = len(g), len(s) i = j = count = 0