🐎作者的话
本文涵盖了浮点型在内存中的如何存储、如何取出、为何有精度丢失等知识点~
跳跃式目录
- 浮点型概括
- 浮点数的存储
- bit位储存模型
- 精度丢失
- 浮点型的取出
- 浮点数的取出实机演示
浮点型概括
常见的浮点型数据有三种:
- 以科学计数法表示的:1e10、1.28e10
- 数据后加入字符‘f’的:3.14f、7.76f
- 不用科学计数法也不加f:1.22、4.89
第一种表示:
1*10^10 和 1.28*10^10
第二种表示:
用float创建的浮点数,要在后面加’f’,不然会默认为double型储。
第三种表示:
用double创建的浮点数,或没加‘f’的float创建数。
浮点数的存储
根据国际标准IEEE754规定,任意的浮点数V都可以表示为以下形式:
- V=(-1)^S * M * 2^E
- S等于0或1,是-1的指数位,0则正数,1则负数
- M等于有效数字,应大于1,小于2
- E是2的指数位,是一个有范围的正数
例:
- V=5.5
- V=9.0
首先我们要知道,十进制的小数点右边第一位,表示10的-1次方,同样,二进制的小数点后一位,是表示2的-1次方。
则V=5.5可以分解成:101.1
则V=9.0可以分解成:1001.0
随后,将这个分解后的数字转为大于1,小于2的数,并将小数点移动了几位记下来,这将是E的大小。
- V=1.011,移动2位,E=2
- V=1.001,移动3位,E=3
最后,如果是正数,S为0,如果是负数,S为1。
- V=(-1)^0 * 1.011 * 2^2
- V=(-1)^0 * 1.001 * 2^3
这样,你就知道如何表示一个浮点型的数了,由此可见,一个浮点型的数,其大小只与>S、M、E三个变量有关,所以在内存中对于浮点型的存储,只需要存储这三个变量可。
bit位储存模型


- 第一张图:float的储存模型
- 第二张图:double的储存模型
- 图片来自比特科技
这两张图相信以各位的聪明才智,不需过多解释也能看得懂。
我们知道,M是一个大于1,小于2的数,那么不同的M之间只有小数点后面的数不同,如果我们只把M小数点后面的数存起来,取出的时候再加上1,就可以多存一位。
因此,float的M能存24位,double的M能存53位。
此外,对于E的存储,还有一些别的规定:
因为E是一个无符号的数,只能是正数,但是科学计数法中是可以出现负数的,所以IEEE又规定,E在存入时必须加上一个中间值。
- 对于float,E有8位,取值范围为0~255,存入时需加上255/2=127.
- 对于double,E有11位,取值范围为0~2047,存入时需加上2047/2=1023.
比如:5.5的E是2,存入时需存2+127=129;9.0的E是3,存入时需存3+127=130.
精度丢失
上述我们说到,二进制小数点后1位是2的-1次方,后2位是2的-2次方…
即,一个浮点型的小数点后面的数,只能用0.5、0.25、0.125…等等数来拼凑起来。
若是我给一个3.141592653579,这在有限的M位下是不可能完整精确地拼凑起来的,于是就有了精度丢失。

Look:我把3.14存进a,鼠标放在上面,显示这个数并不是精准的3.14.
这也是为什么,double型能存的数据比float型更为精准。(因为M位更多)
浮点型的取出
- S的取出:没什么好说的,是1还是1,是0还是0.
- M的取出:因为只存了小数点后面,取出来后要加上1.
- E的取出:又分为三种情况,请看细细道来。
1,E全为1,此时若M全是0,则是无穷大,正负看S;若M不全是0,则这个数是NaN(未定义或不可表示的值),至于为什么,我只能说这是未尽事宜,是规定。
2,E全为0,这种情况下在取出E时,float规定E为-126,double规定E为-1022,M取出来后不再加上1,以此来表示一个无限接近于0的数,正负看S。
3,E不全0也不全1,减去127或1023拿出来即可。
浮点数的取出实机演示

如图,我将5.5f存入a;
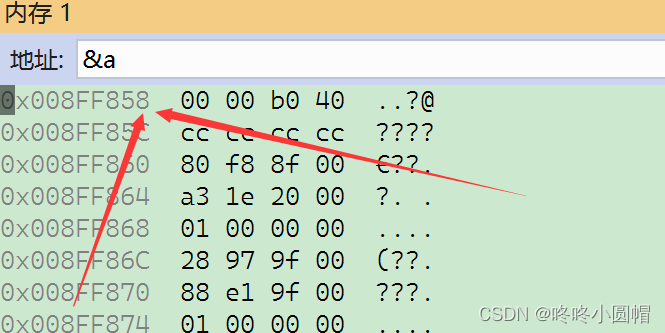
随后,取a的地址进行观察。
因为我当前环境是x86,机器为小端存储。
PS:如果您不明白什么是小端存储,请点击:大小端字节序存储详解
所以a的地址存放的十六进制序列为:40B00000
转换为二进制:0 10000001 01100000000000000000000
观察S、M、E的位置
S:0
E:因为不全是1或全是0,应减去127,0b10000001-127=2
M:0.011+1=1.011
这样,你就把V取出来了。
这时候有同学可能要问了,这把SME三个数装上以后,是1.011*2^2是4.011啊。
请注意:此时是用二进制表示
📖博客主页:咚咚小圆帽的CSDN主页
🎁感谢您的:👍点赞⭐️收藏❤️关注🔗转发~
📚所属专栏:C语言进阶
📑相关文章:整型在数据中的存储
🔖今日寄语: 好好学习,天天向上~
⚠️本文由咚咚小圆帽于2023年1月12日在CSDN原创首发
🌏欢迎各位指出错误,非常感谢~