🏠关于此专栏：Super数据结构专栏将使用C/C++语言介绍顺序表、链表、栈、队列等数据结构，每篇博文会使用尽可能多的代码片段+图片的方式。
🚪归属专栏：Super数据结构
🎯每日努力一点点，技术累计看得见

---

二叉树的非递归遍历

前序遍历

首先看一下前序遍历的递归实现代码↓↓↓

typedef int BTDataType;

typedef struct BTNode
{
	BTNode* _left;
	BTNode* _right;
	BTDataType _data;
}BTNode;

void PreOrder(BTNode* root)
{
	if(rott == NULL)return;
	printf("%d ", root->_data;)
	PreOrder(root->_left);
	PreOrder(root->_right);
}

在进行前序遍历时，先访问节点再遍历其左子树，后遍历其右子树。但递归实现时，由于栈区空间空间通常只有1MB（1024*1024字节），如果二叉树的高度过大，递归时会不断建立栈帧，当超出栈区容量，则会出现栈溢出的情况。并且，建立栈帧和销毁栈帧会出现大量的时间消耗，因而递归实现的效率并不高。

为了规避栈溢出及递归实现效率不高的问题，我们可以使用非递归实现方式。那非递归实现要怎么写呢？

在该文章前，我们介绍了一个结构——栈。我们可以借助栈结构来实现非递归遍历。下面给出一颗二叉树，并逐步分析前序遍历的非递归实现过程↓↓↓

1.对下图的二叉树进行非递归遍历。当我们访问根节点（值为1）后，如果它的右子树不为空，则先将它的右子树根节点（值为4）保存到栈中，再进入它的左子树中。（ps：保存当前节点的指针为cur）

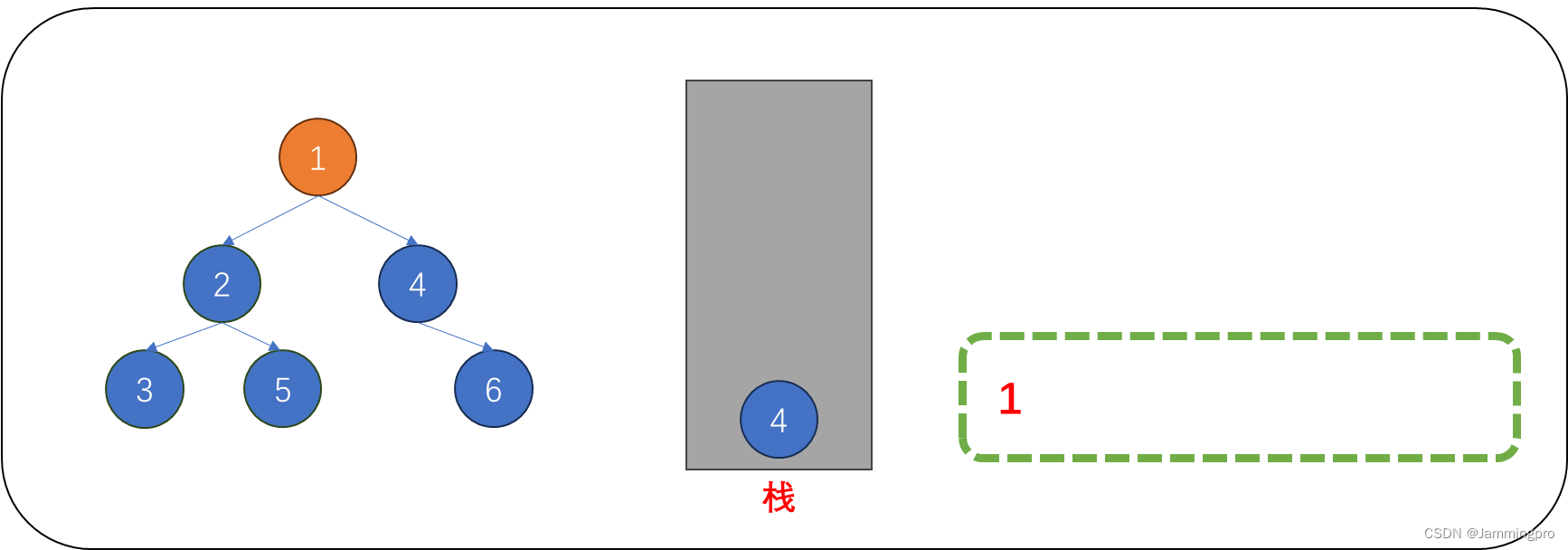
2.访问值为2的节点后，如果它的右子树不为空，则先将它的右子树根节点（值为5）保存到栈中，再进入它的左子树。

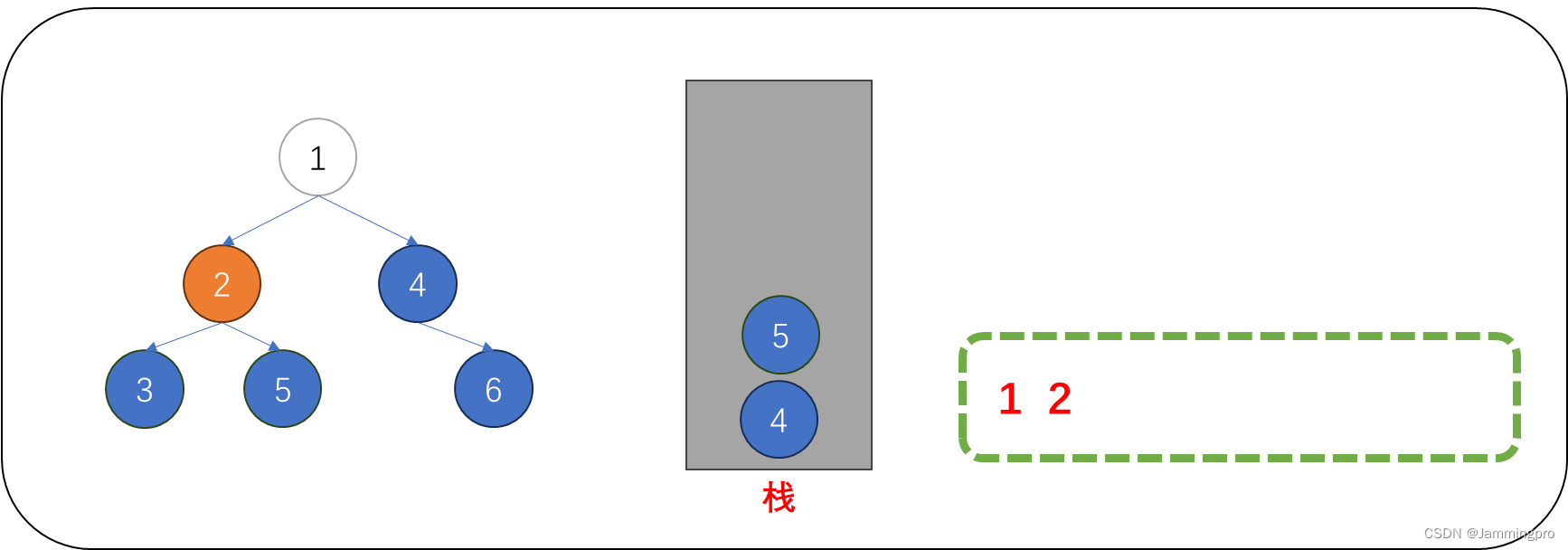
3.访问值为3的节点后，由于它达地右子树为空。因此，不必将它的右子树入栈。接着再进入值为3的节点的左子树。

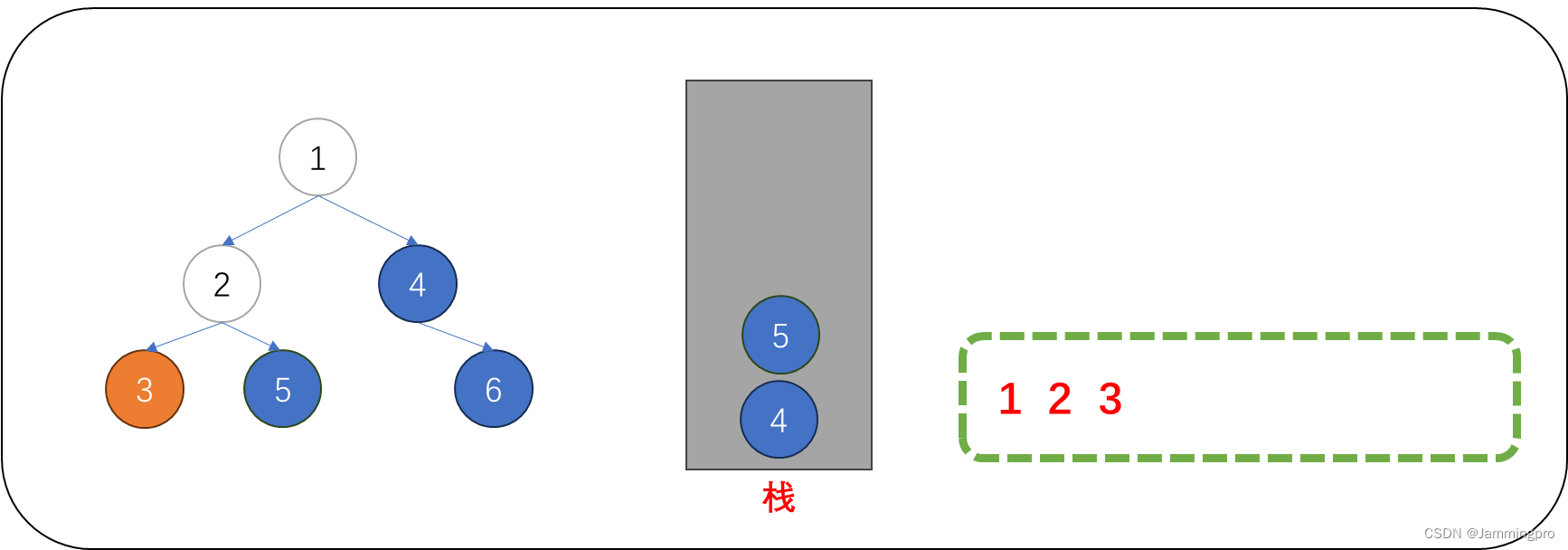
4.此时，当前节点指针cur为空。我们需要从栈里获取栈顶元素。可以发现，弹出栈的节点正是值为2的节点的右子树；此时，值为2的节点的左子树已经访问完毕。在访问值为5节点后，由于它的右子树为空，因此不用入栈。接着将当前节点的指针跳转到值为5的节点的左子树。

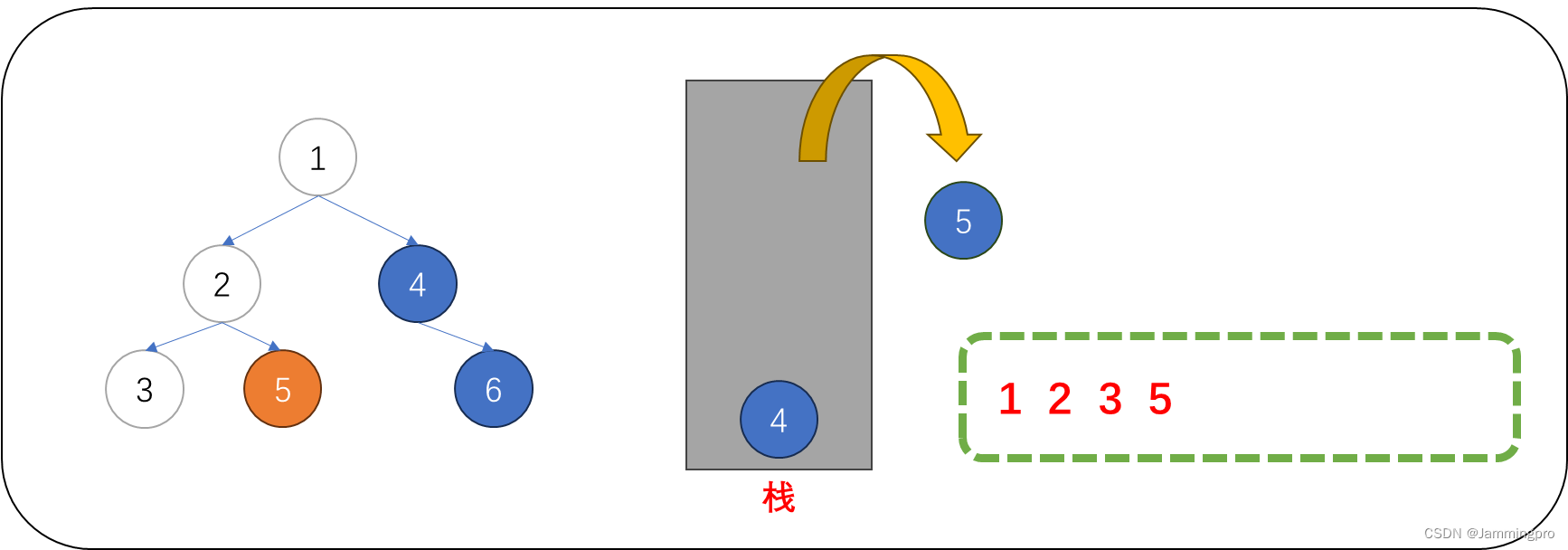
5.此时，当前节点指针cur为空，我们需要从栈中获取栈顶元素。可以发现，弹出栈的节点正式根节点的右子树的根节点；而在获取该节点时，根节点的左子树已经访问完毕。访问值为4的节点后，将它的右子树根节点入栈。再将当前节点指针cur跳转到指针4的节点的左子树。

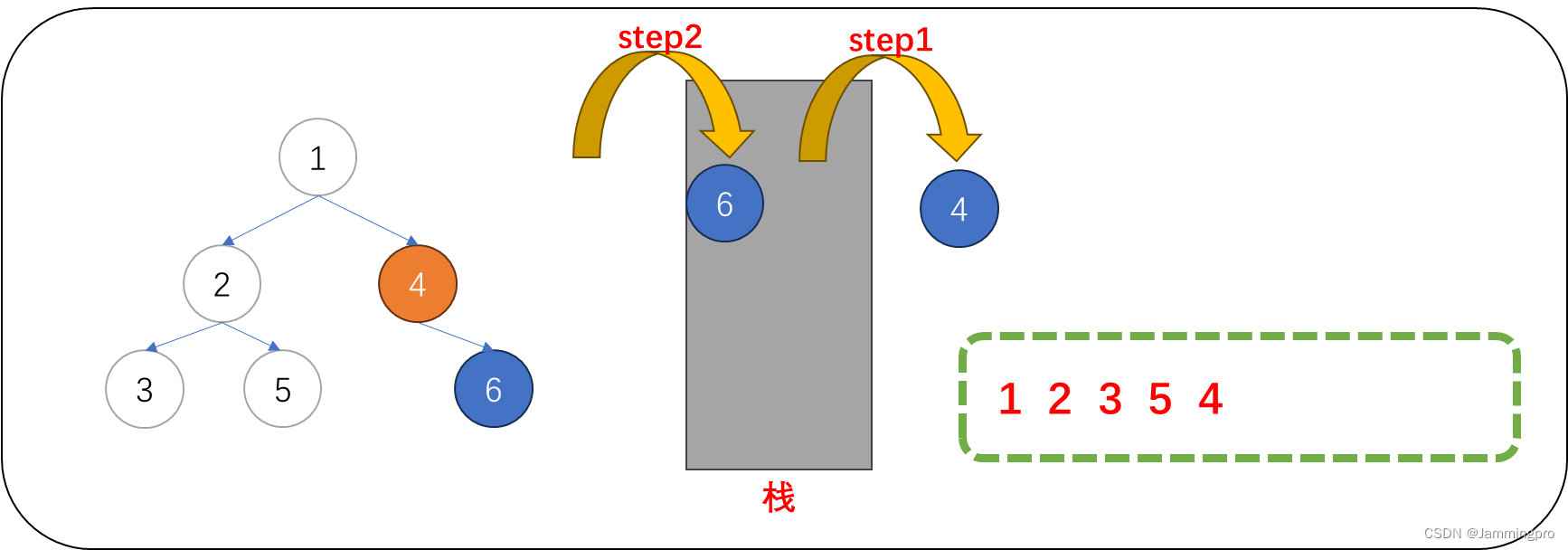
6.此时，当前节点指针cur为空，则需要获取栈顶元素（即值为6的节点）。再访问值为6的节点后，由于它的右子树为空，因此不用入栈。再将当前节点栈帧跳转到左子树节点。

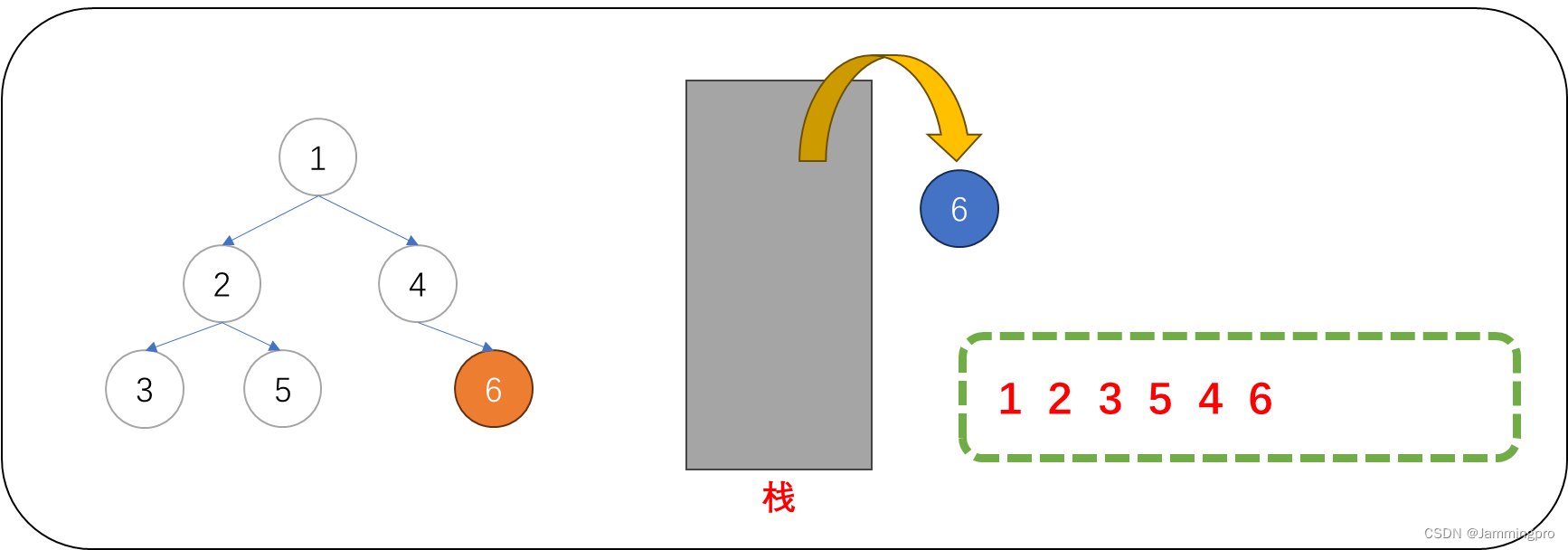
7.此时，当前节点指针cur为空，栈为空，则前序遍历结束。

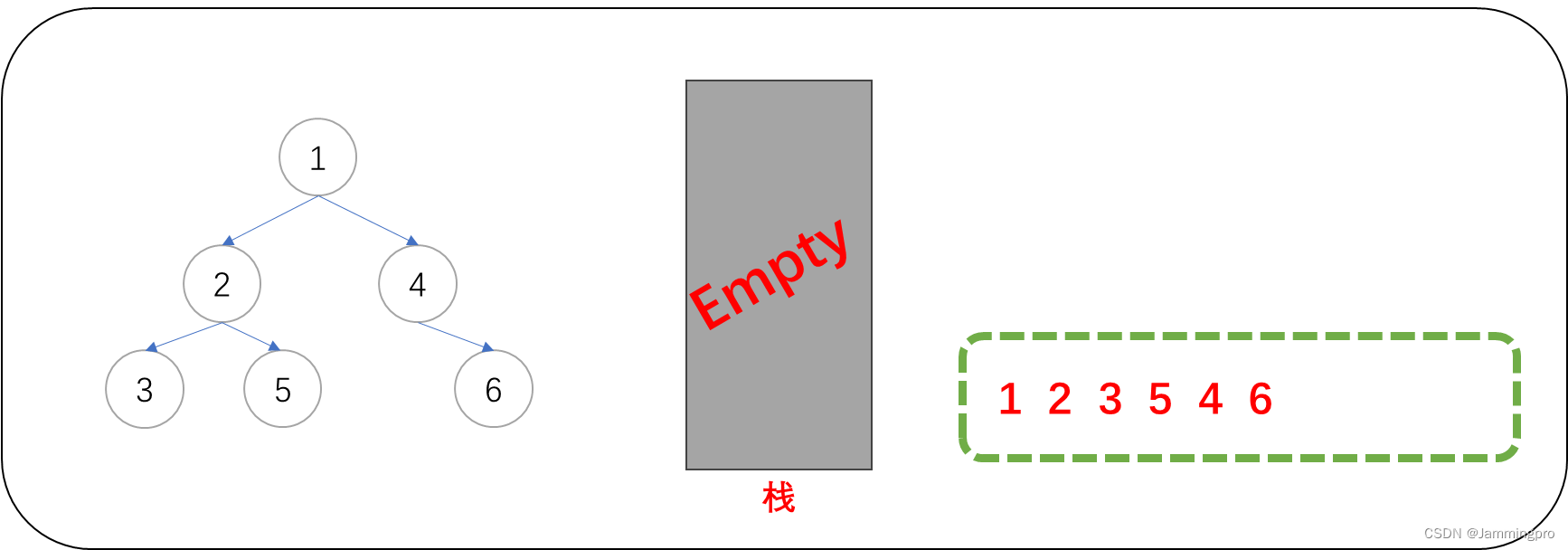
由上面的前序遍历非递归实现示例分析可知：在访问某个节点后，要跳转到它的左子树前，要先将它的右子树根节点保存到栈中（如果右子树非空的情况下）。当栈为空且当前节点指针为空的时候，整个遍历过程结束。

[LeetCode-二叉树的前序遍历]
下面给出前序遍历的非递归实现代码↓↓↓

class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        vector<int> ret;
        stack<TreeNode*>stk;
        TreeNode* cur = root;

        while(cur || !stk.empty())
        {
            while(cur)
            {
                ret.push_back(cur->val);
                if(cur->right)
                {
                    stk.push(cur->right);
                }
                cur = cur->left;
            }
            if(!stk.empty())
            {
                cur = stk.top();
                stk.pop();
            }
        }
        return ret;
    }
};

中序遍历

首先看一下中序遍历的递归实现代码↓↓↓

void InOrder(BTNode* node)
{
	if(node == nullptr) return;
	InOrder(node->_left);
	cout << node->_val << " ";
	InOrder(node->_right);
}

中序遍历时，遇到节点是并不立即访问，而是将它的左子树访问完毕后，才会访问当前节点。因此，我们需要后面访问的节点可以先将其保存到栈中，等其左子树遍历完毕后，再从栈中取出访问。

下面给出一颗二叉树，并使用它演示中序遍历非递归遍历的执行过程↓↓↓

1.当访问根节点时，由于它的左子树尚未访问完毕，则需要将它先保存当栈中。再当前节点指针跳转至它的左子树。

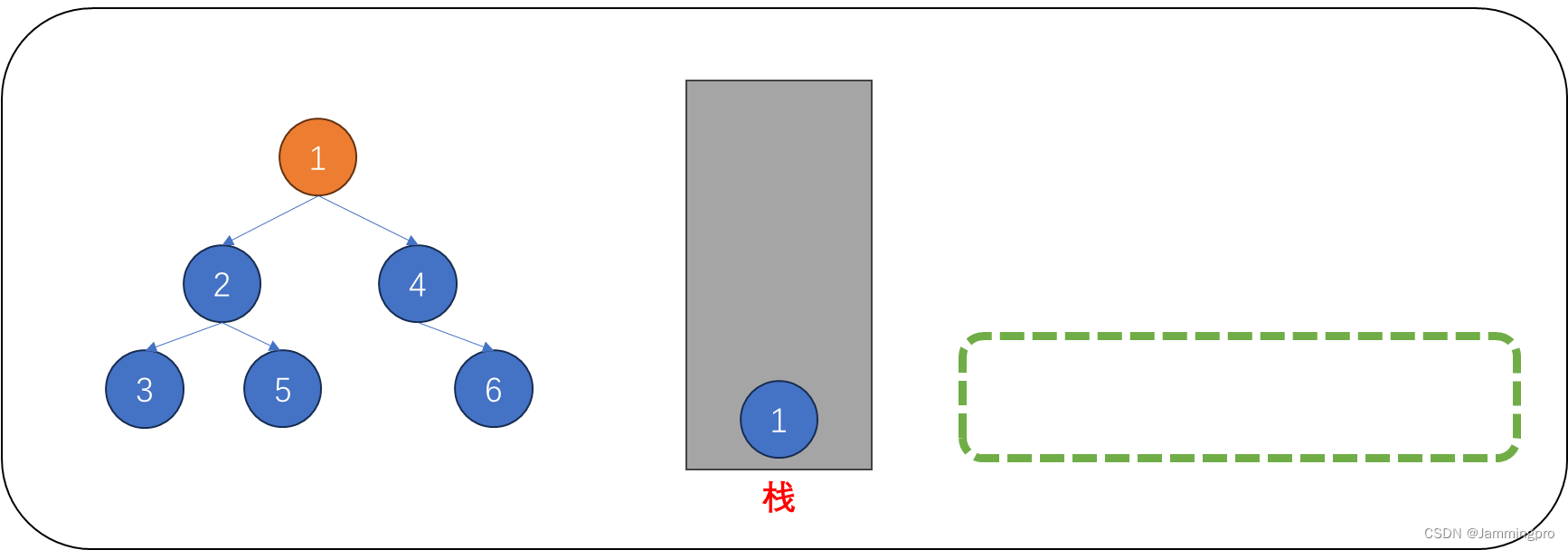
2.当访问指针为2的节点时，它的左子树也未访问完毕，则需要将它保存到栈中。再当前节点指针跳转至它的左子树。

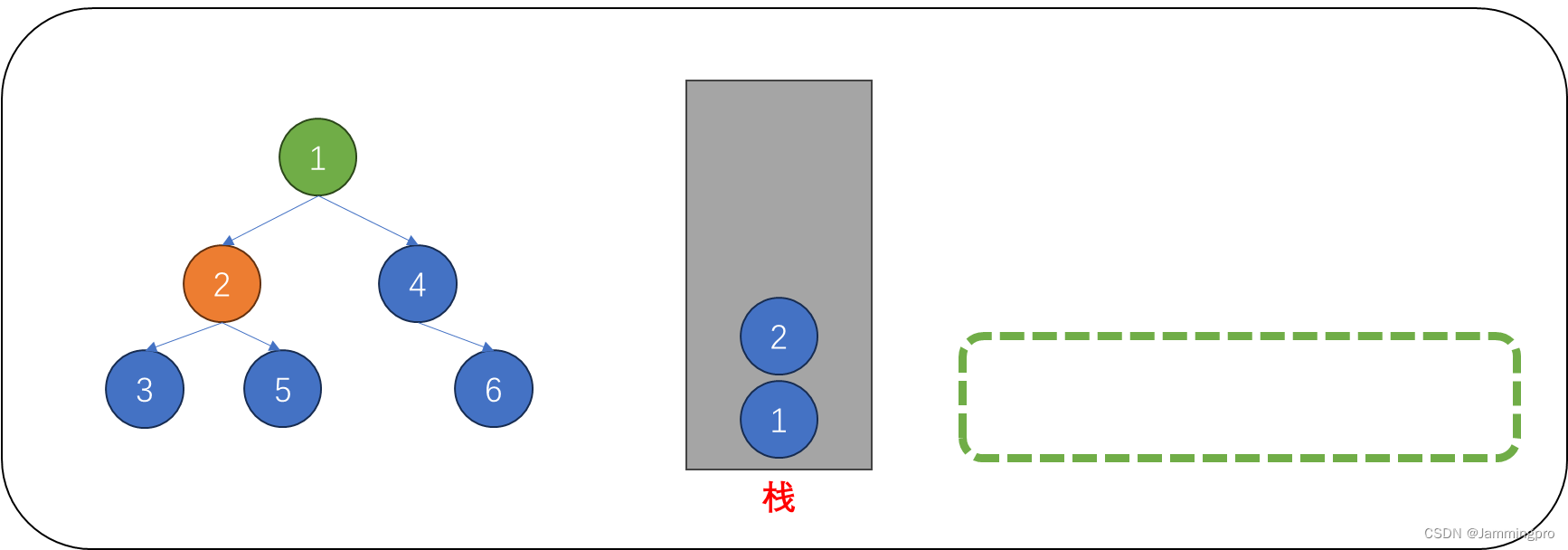
3.在访问值为3的节点时，我们暂时没有对它的左子树进行访问（即没有对它做判断），即使它为空。因而，我们也需要将节点3入栈。

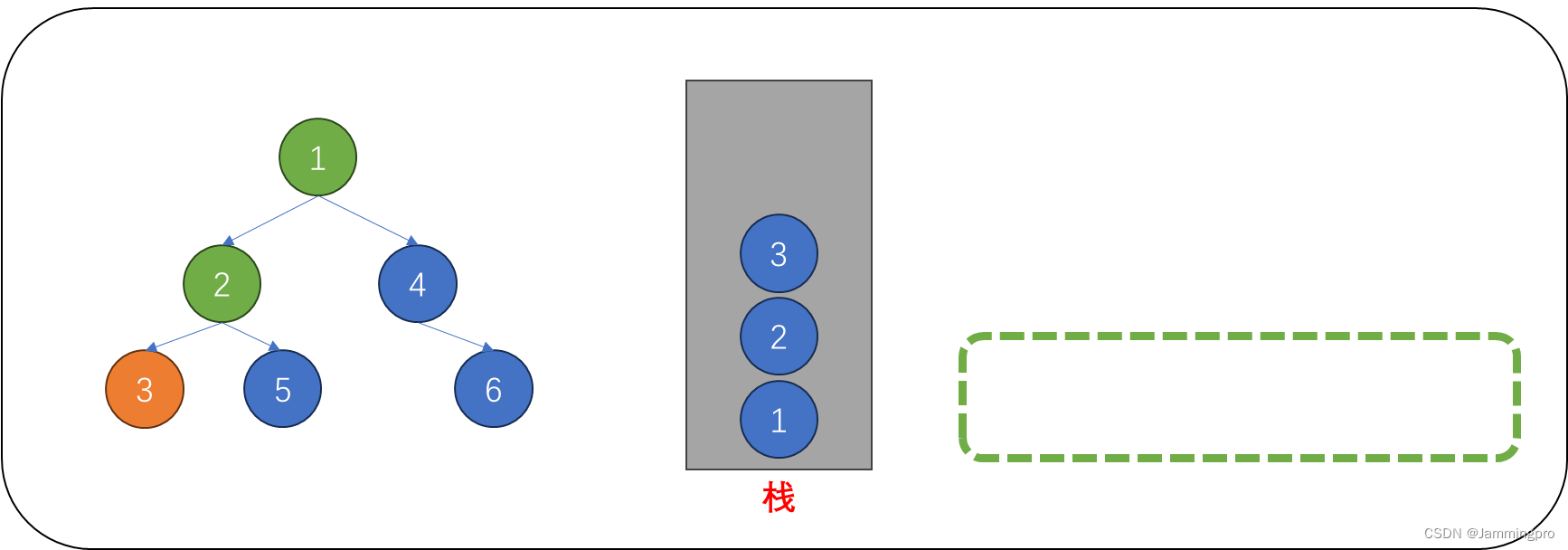
4.此时当前节点指针为空，则需要从栈顶获取元素进行访问。从栈中取出的节点，它的左子树一定访问过了。此时我们可以访问该节点（即值为3的节点）。该节点的左子树访问完，该节点也被访问了，则需要访问它的右子树，则需要将当前节点指针cur指向该节点的右子树根节点。

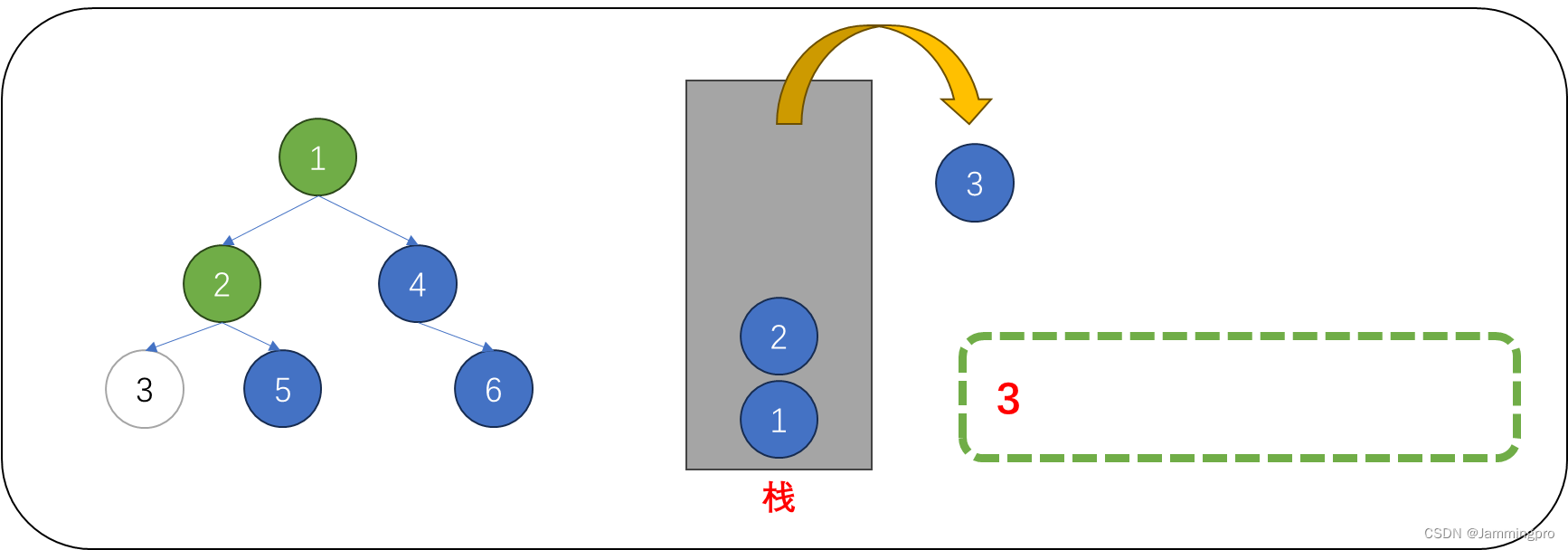
5.此时当前节点指针cur为空，则需要从栈顶获取元素进行访问，从栈中取出的节点，它的左子树一定访问过了。此时我们可以访问该节点（即值为2的节点）。该节点的左子树访问完，该节点也被访问了，则需要访问它的右子树，则需要将当前节点指针cur指向该节点的右子树根节点。

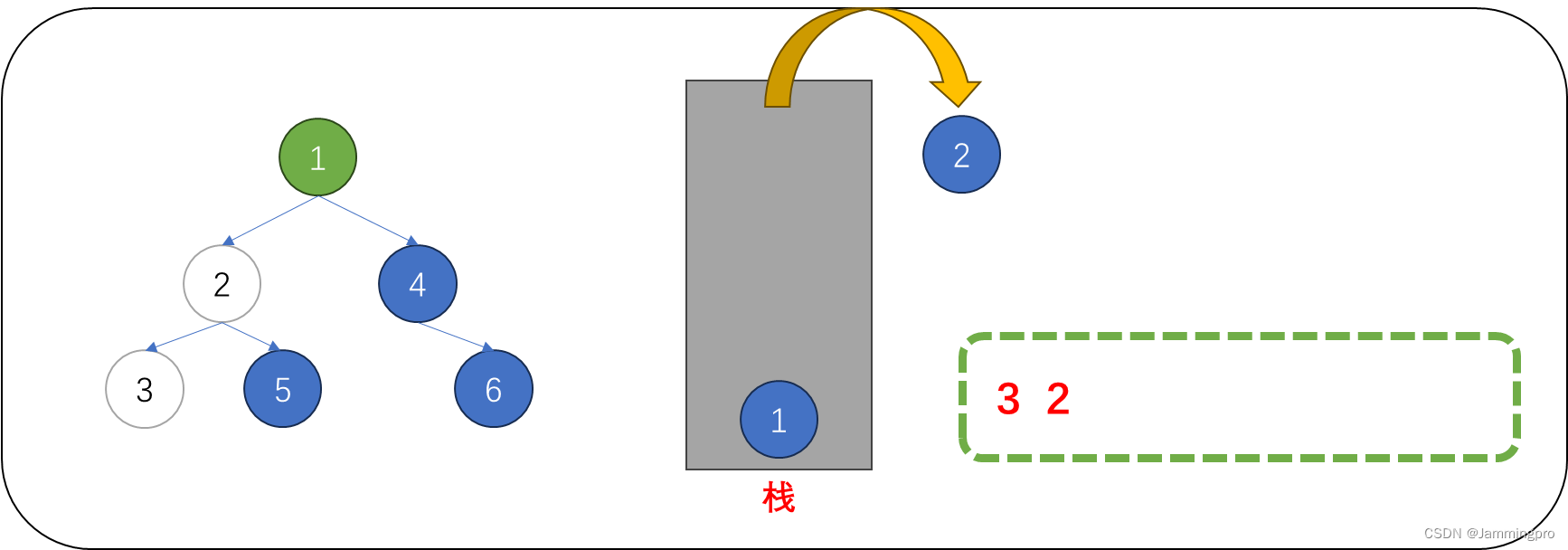
6.当前节点指针cur指向值为5的节点，但该节点的左子树尚未被访问（即程序暂未对它的左子树做判断），因此需要将当前节点先入栈，并将cur指针指向该节点的左子树根节点。

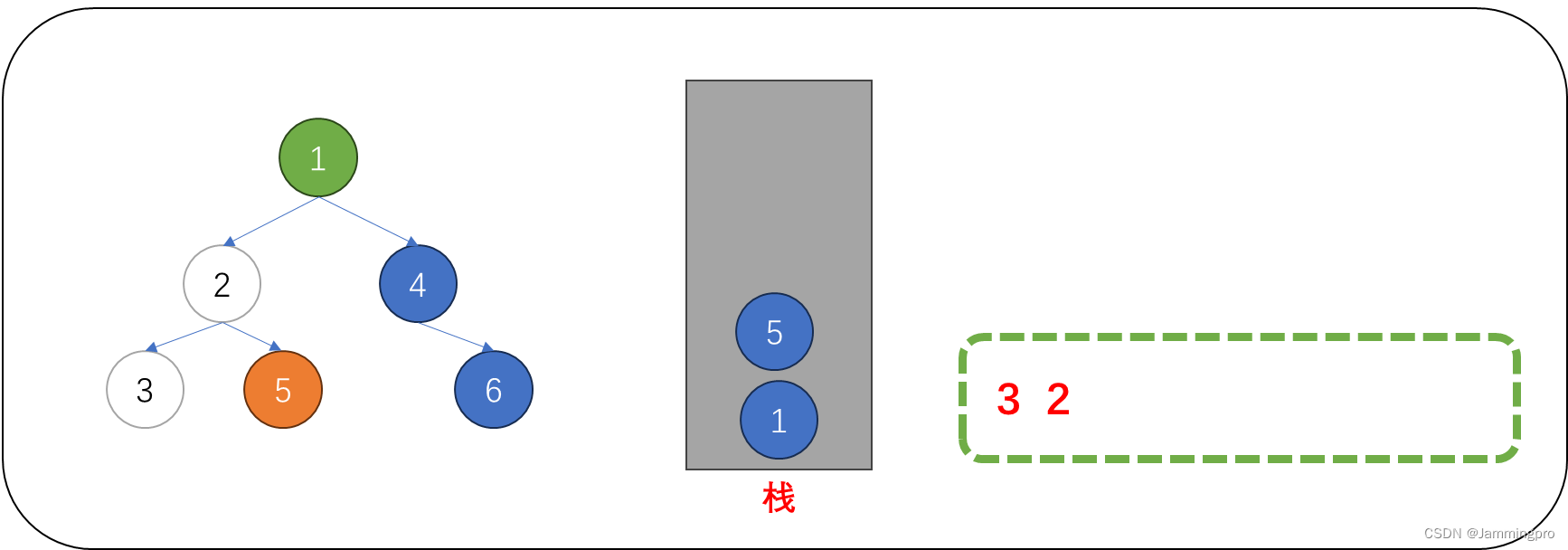
7.此时当前节点指针cur为空，则需要获取栈顶元素（值为5的节点）。栈中元素的左子树一定被访问结束，此时可以访问该节点的值，访问后，需要继续遍历它的右子树，即cur=cur->_right。

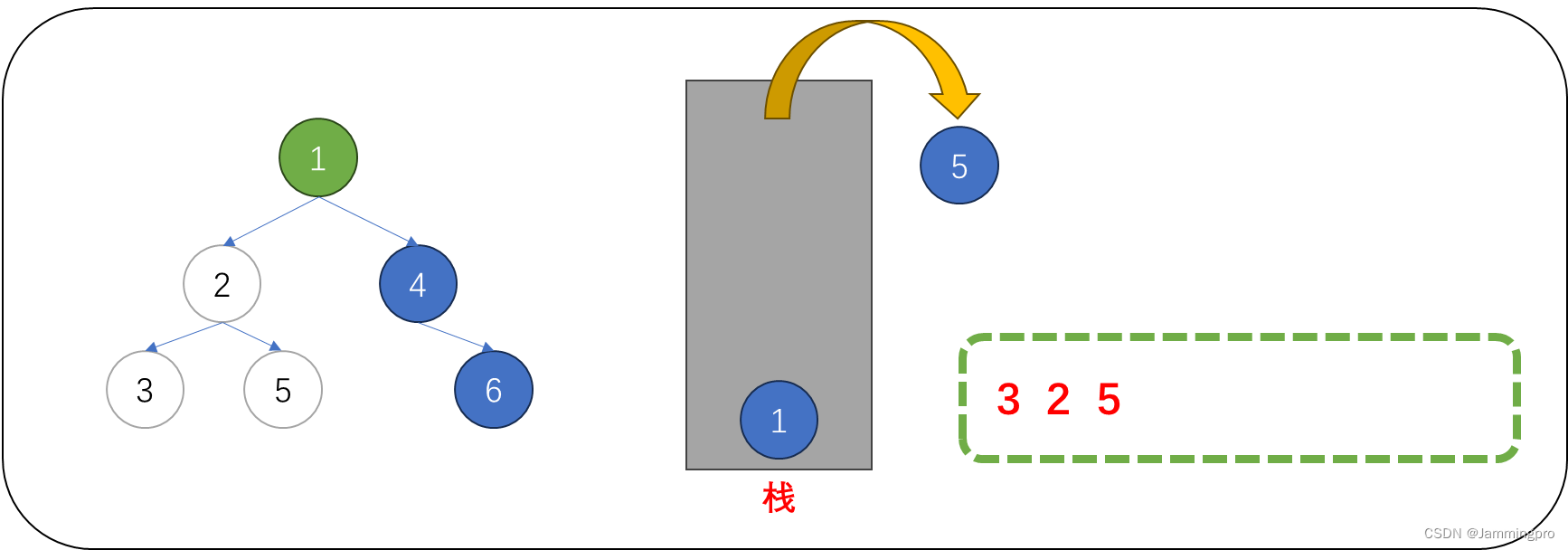
8.此时当前节点指针cur为空，则需要获取栈顶元素（值为1的节点）。栈中元素的左子树一定被访问结束，此时可以访问该节点的值，访问结束后需要继续遍历它的右子树，即cur=cur->_right。

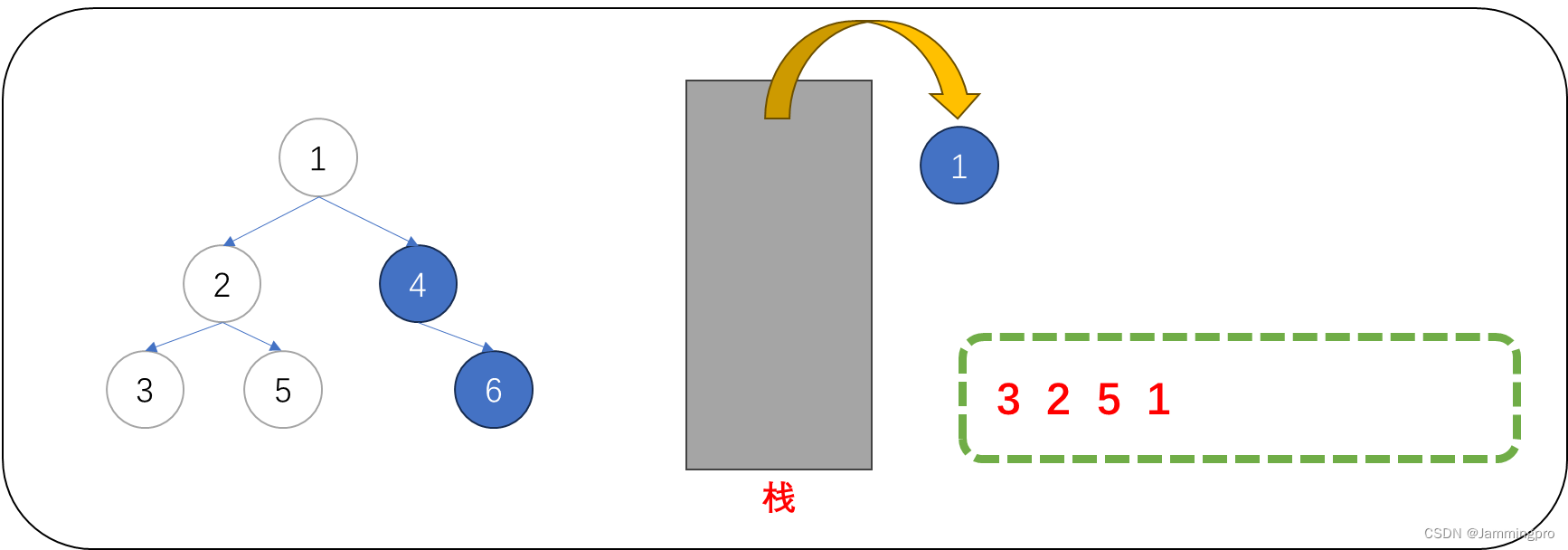
9.此时当前节点指针指向值为4的节点，该节点的左子树尚未被访问（即该节点的左子树尚未被判断），此时需要将该节点保存到栈中，并将cur=cur->_left。

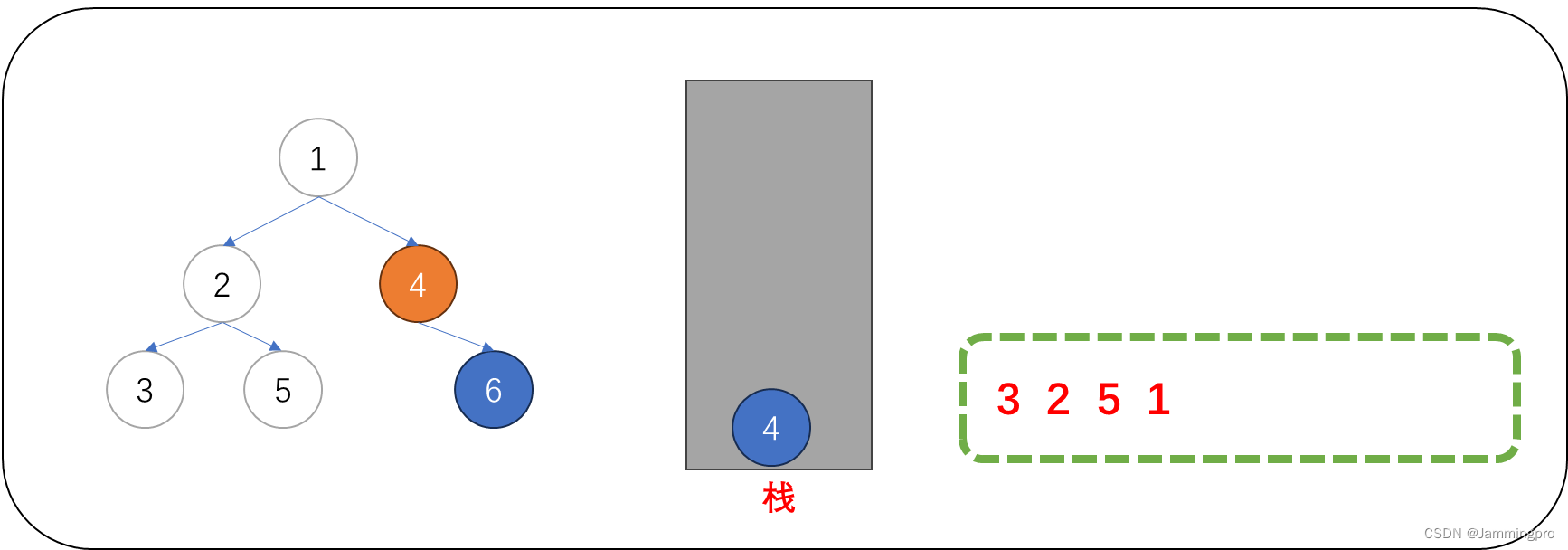
10.此时当前节点指针为空，需要获取栈顶元素，栈顶元素的左子树一定访问结束了。此时可以直接访问该节点的值，访问结束后，要继续遍历它的右子树。

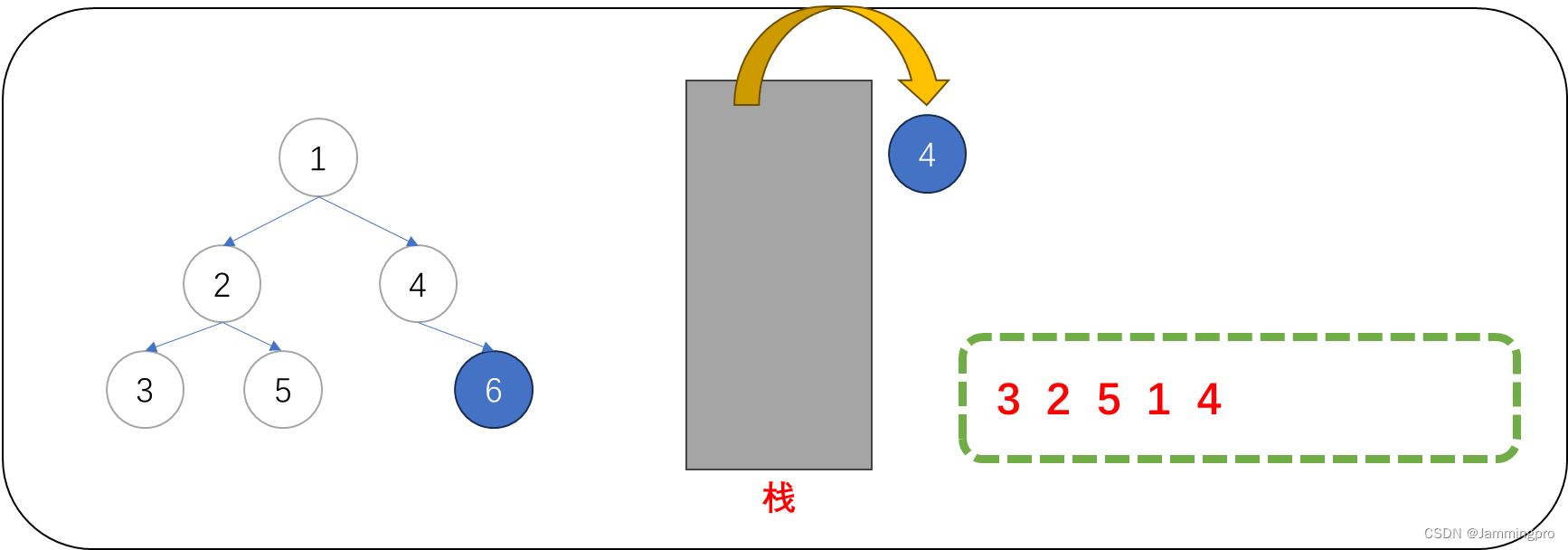
11.当前节点指针cur指向值为6的节点，由于它的左子树尚未被遍历（尚未被判断），需要先将该节点入栈后，cur=cur->_left。

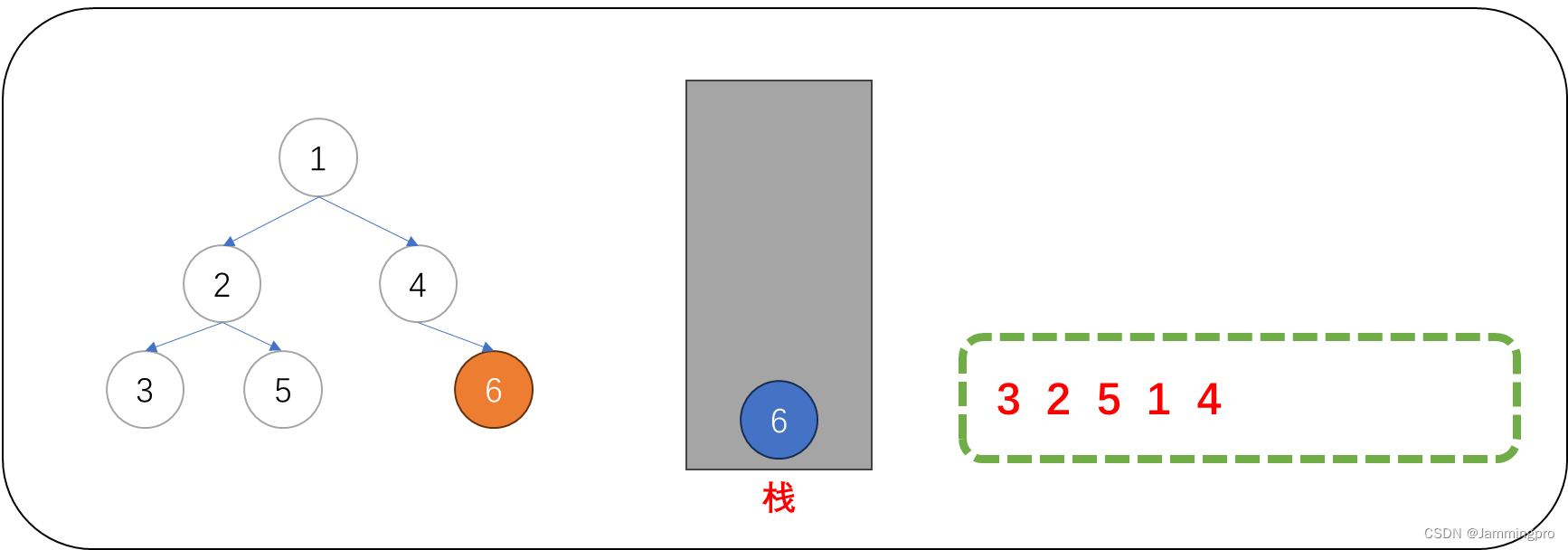
12.此时当前节点指针为空，需要获取栈顶元素，栈顶元素的左子树一定访问结束了。此时可以直接访问该节点的值（值为6的节点），访问结束后，要继续遍历它的右子树。

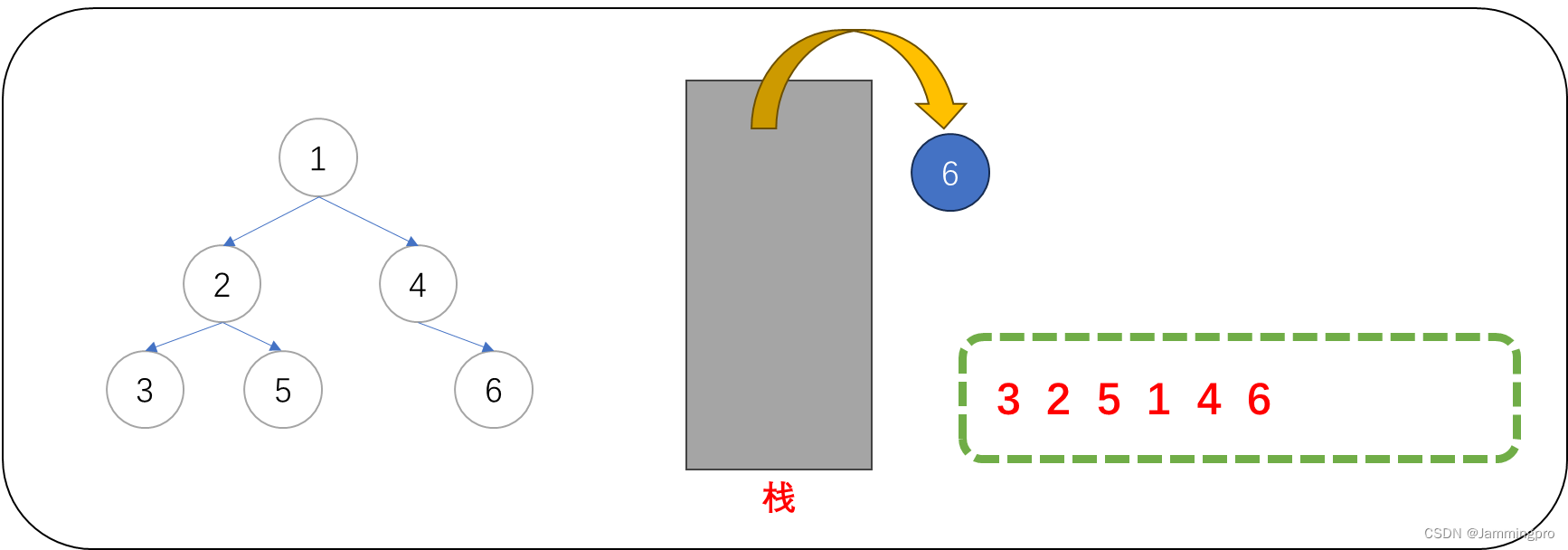
13.此时当前节点指针cur为空，栈为空，则遍历结束。

中序遍历的思想就是，遇到节点时先不访问，因为它的左子树尚未访问完毕，所以需要将它先入栈。当前节点指针一定为空时，为空的情况其实是：当前节点指针访问的正是某个叶子节点的左子树，并表示该节点的左子树访问完毕。再从栈里取出节点，栈中取出节点的左子树一定被访问结束了，可以访问该节点了。该节点访问完毕后，我们无法保证该节点的右子树已经访问完毕，因此需要将当前节点指针cur指向该节点的右子树，重复上述操作。

[LeetCode-二叉树的非递归遍历]
下面给出中序遍历非递归遍历代码↓↓↓

class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> ret;
        stack<TreeNode*> stk;
        TreeNode* cur = root;
        while(cur || !stk.empty())
        {
            while(cur)
            {
                stk.push(cur);
                cur = cur->left;
            }
            if(!stk.empty())
            {
                cur = stk.top();
                stk.pop();
                ret.push_back(cur->val);
                cur = cur->right;
            }
        }
        return ret;
    }
};

后序遍历

在介绍后序遍历的非递归实现前，先看下一它的递归实现↓↓↓

void PostOrder(BTNode* node)
{
	if(node == nullptr) return;
	PostOrder(node->_left);
	PostOrder(node->right);
	cout << node->_val << " ";
}

下面我们使用一颗二叉树，演示后序遍历的非递归遍历执行过程↓↓↓

1.后序遍历相比前/中序遍历，需要多一个指针preVisit，用于记录上次访问的节点，初始时为空。当前节点cur指向根节点，一开始就需要不断执行cur=cur->_left将所有最左节点全部入栈。

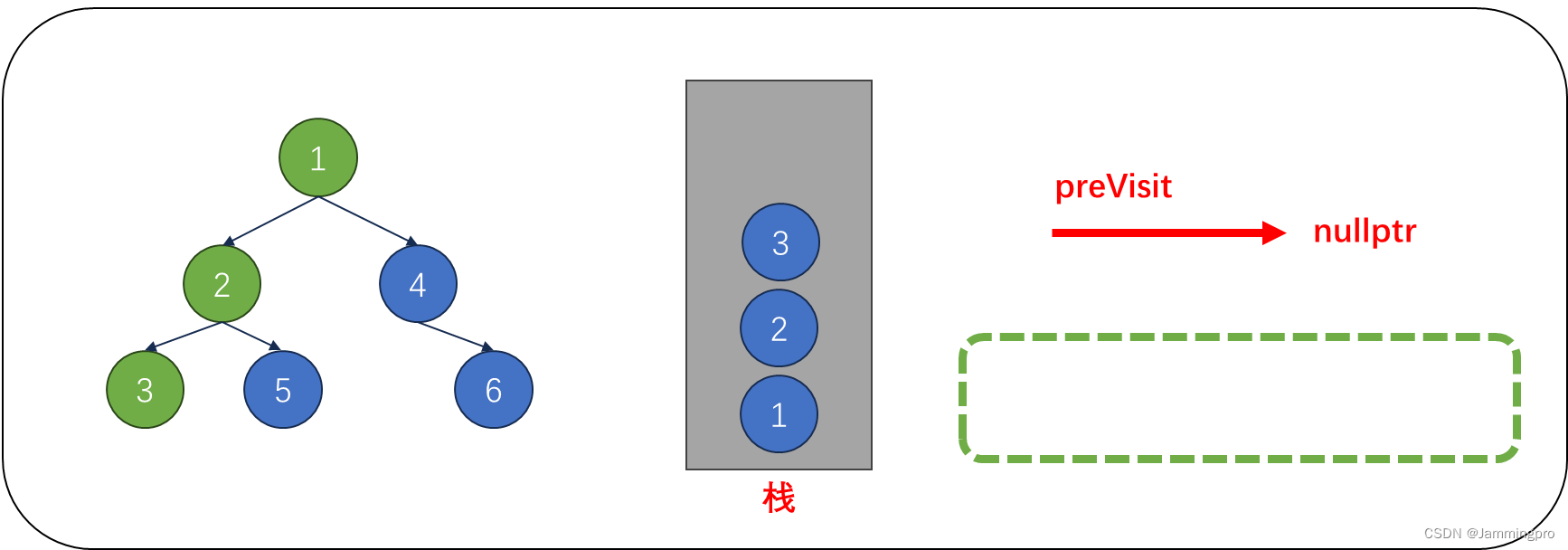
2.当cur为空时，取出栈顶元素，cur=栈顶结点。由于，我们一遇到一个结点，将它的最左侧结点全部入栈，则栈中取出的结点左子树已经被访问过了。如果cur->right==nullptr || cur->right==preVisit表示该节点的右子树已经访问过了或为叶子节点。此时值为3的结点满足，则可以访问该节点。访问完该结点后，preVisit=值为3的结点。访问完该节点后，将cur指向栈顶元素。

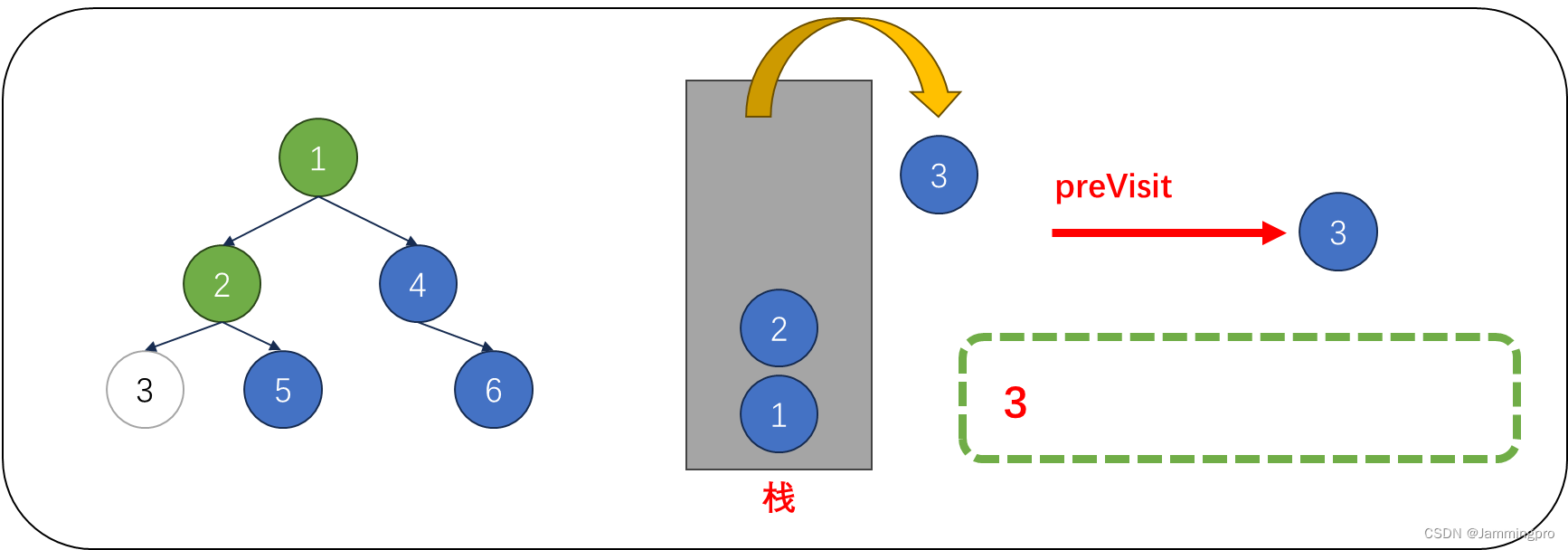
3.此时cur指向值为2的结点，由于当前cur不满足cur->right==nullptr || cur->right==preVisit，则表明该结点的右子树尚未被访问，则不能将该结点出栈。而是将cur指向栈顶元素的右孩子，即值为5的结点。获取栈顶元素右子树根节点指针后，会将该右子树的最左侧节点全部入栈。

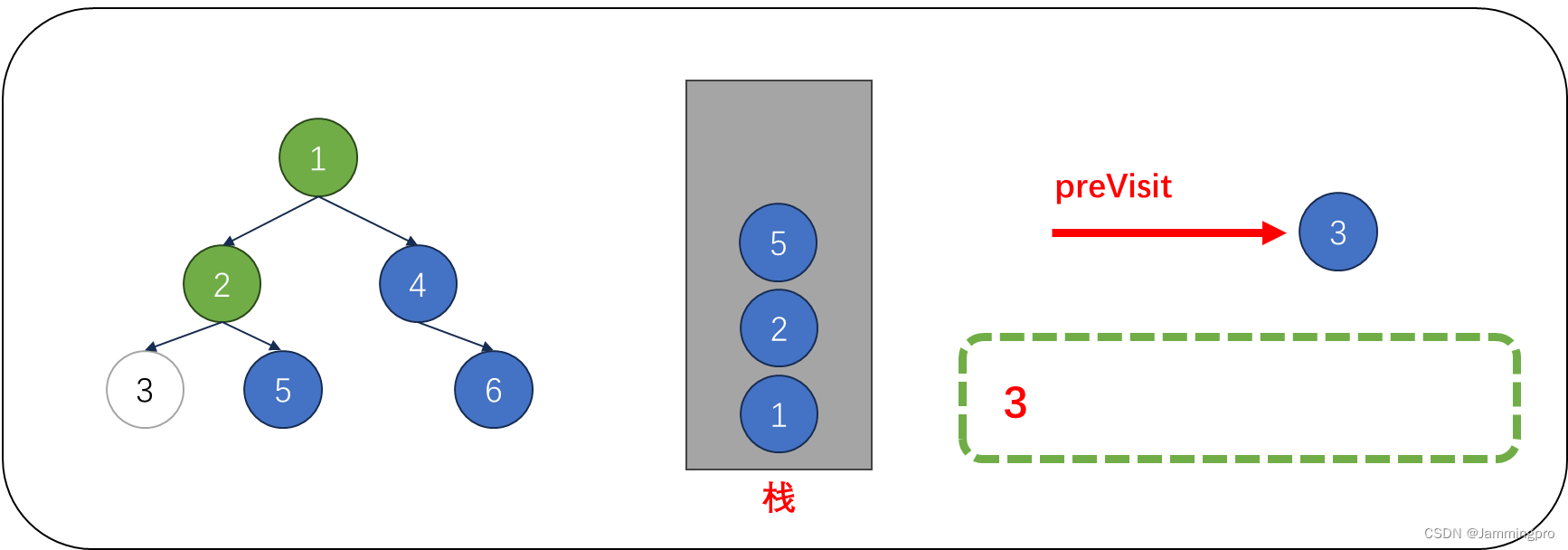
4.此时cur为空，从栈顶获取值为5的节点，由于cur满足cur->right==nullptr || cur->right==preVisit，则表明该结点的右子树已经被访问或为叶子节点，则值为5的节点可以出栈。并将上次访问节点指针preVisit改为值为5的节点。cur指向栈顶元素。

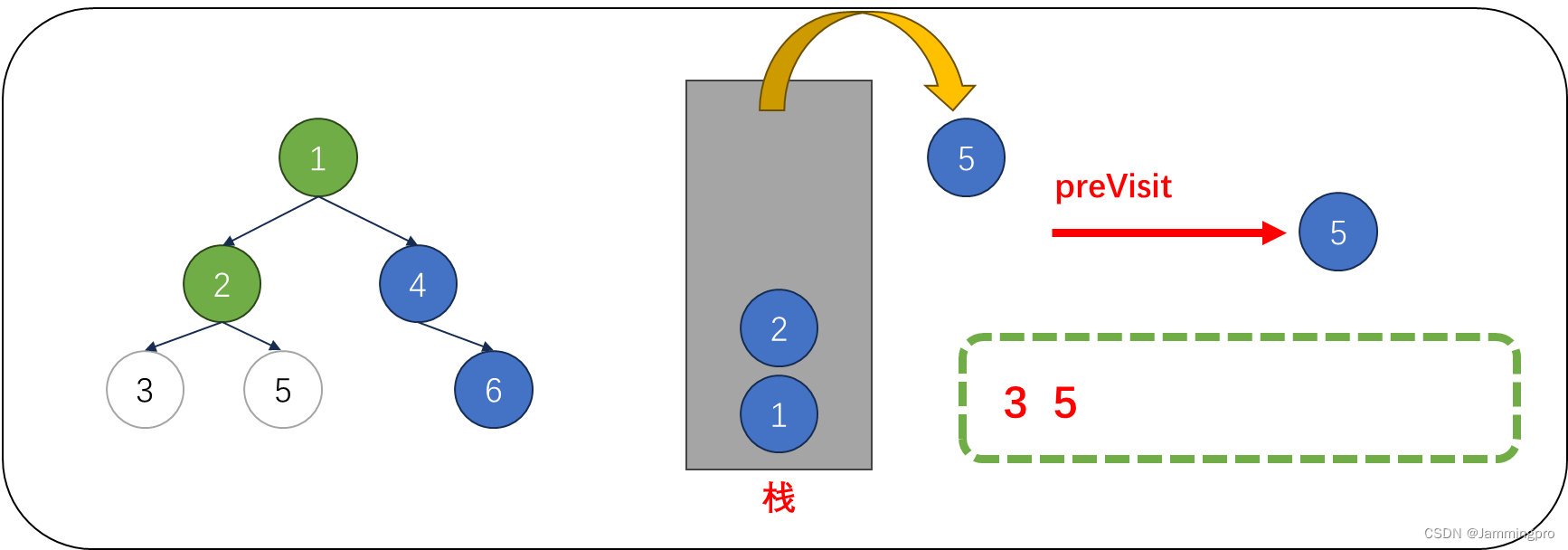
5.此时cur指向值为2的节点，由于cur->right==nullptr || cur->right==preVisit，则表明该结点的右子树已经被访问或为叶子节点，则值为2的节点可以出栈。并将上次访问节点指针preVisit改为值为2的节点。cur指向栈顶元素。

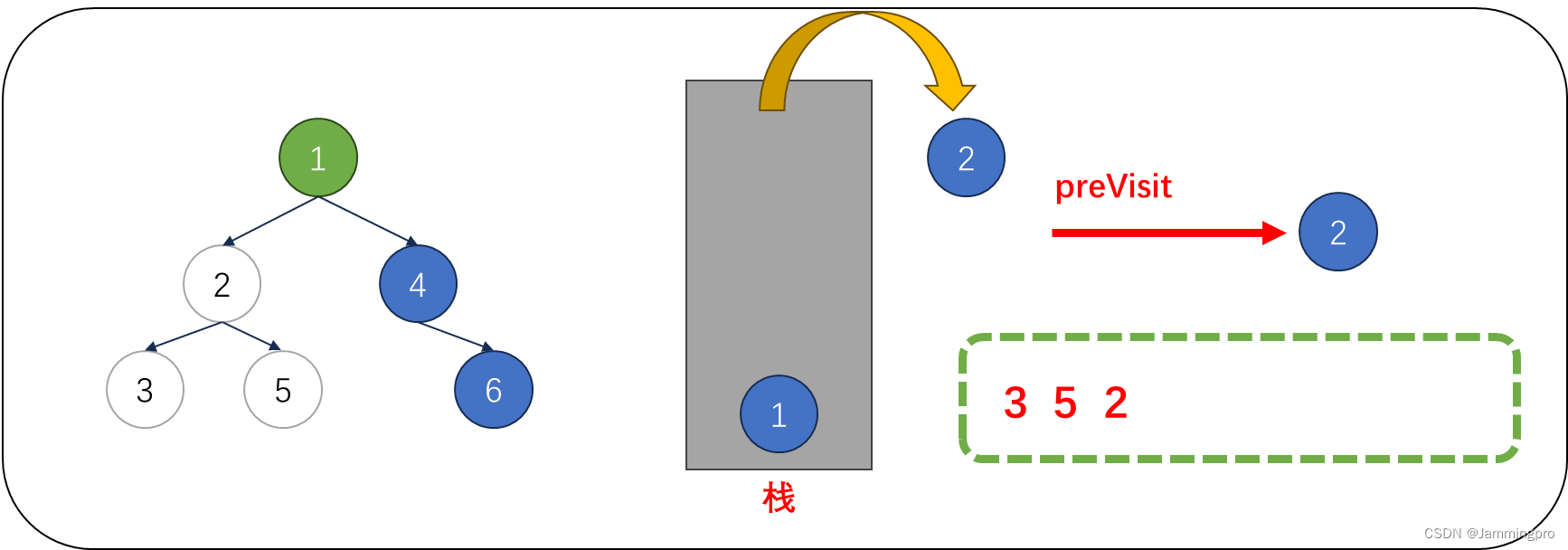
6.此时cur指向值为1的结点，由于当前cur不满足cur->right==nullptr || cur->right==preVisit，则表明该结点的右子树尚未被访问，则不能将该结点出栈。而是将cur指向栈顶元素的右孩子，即值为4的结点。获取栈顶元素右子树根节点指针后，会将该右子树的最左侧节点全部入栈。

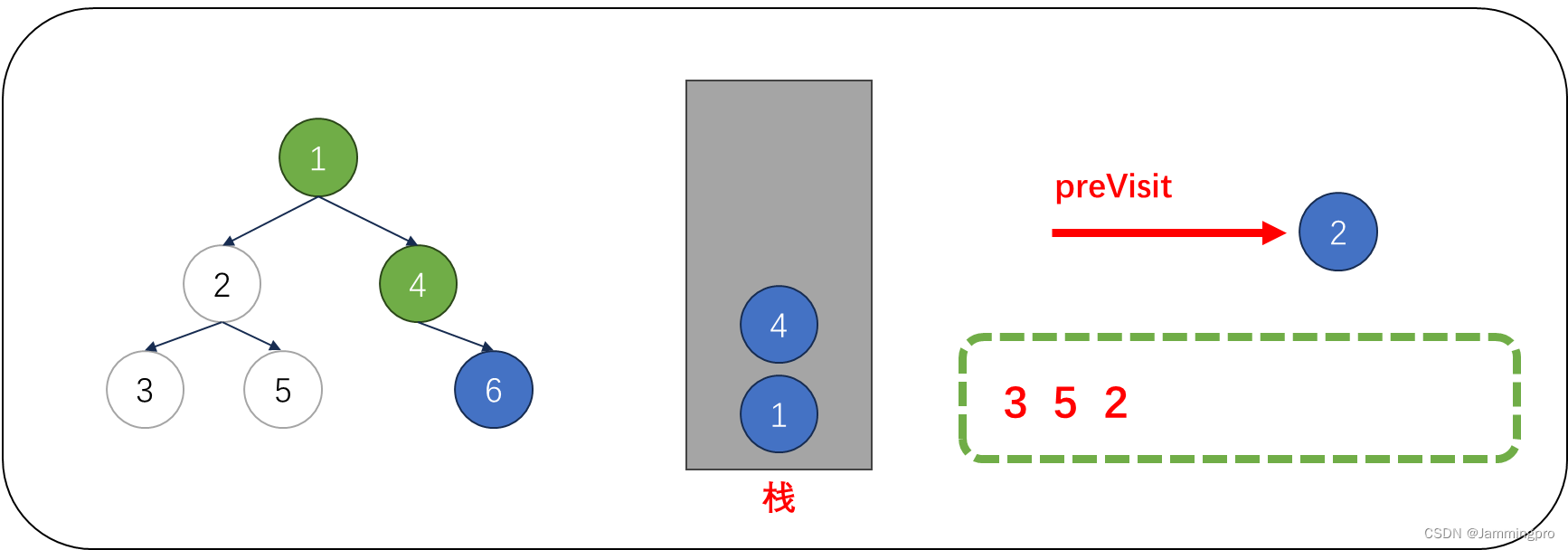
7.此时cur为空，从栈顶获取值为4的节点，由于cur不满足cur->right==nullptr || cur->right==preVisit，则表明该结点的右子树尚未被访问，则不能将该结点出栈。而是将cur指向栈顶元素的右孩子，即值为6的结点。获取栈顶元素右子树根节点指针后，会将该右子树的最左侧节点全部入栈。

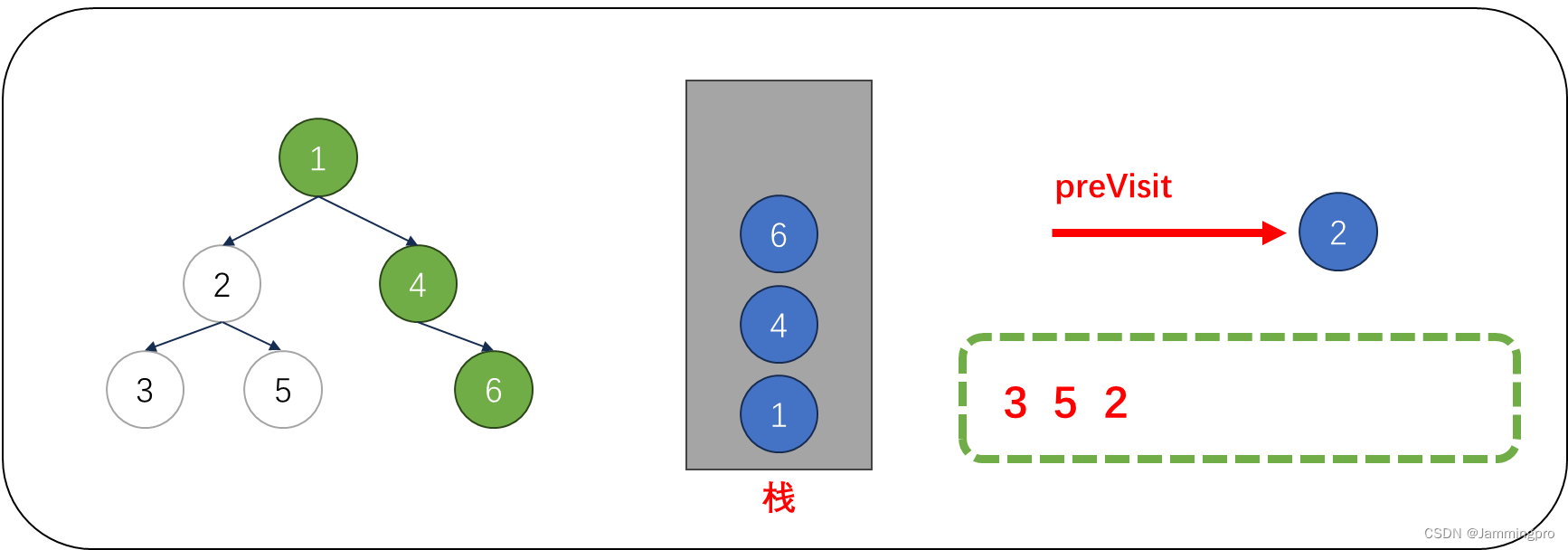
8.此时cur为空，从栈顶获取值为6的节点，由于cur满足cur->right==nullptr || cur->right==preVisit，则表明该结点的右子树已经被访问或为叶子节点，则值为6的节点可以出栈。并将上次访问节点指针preVisit改为值为6的节点。cur指向栈顶元素。

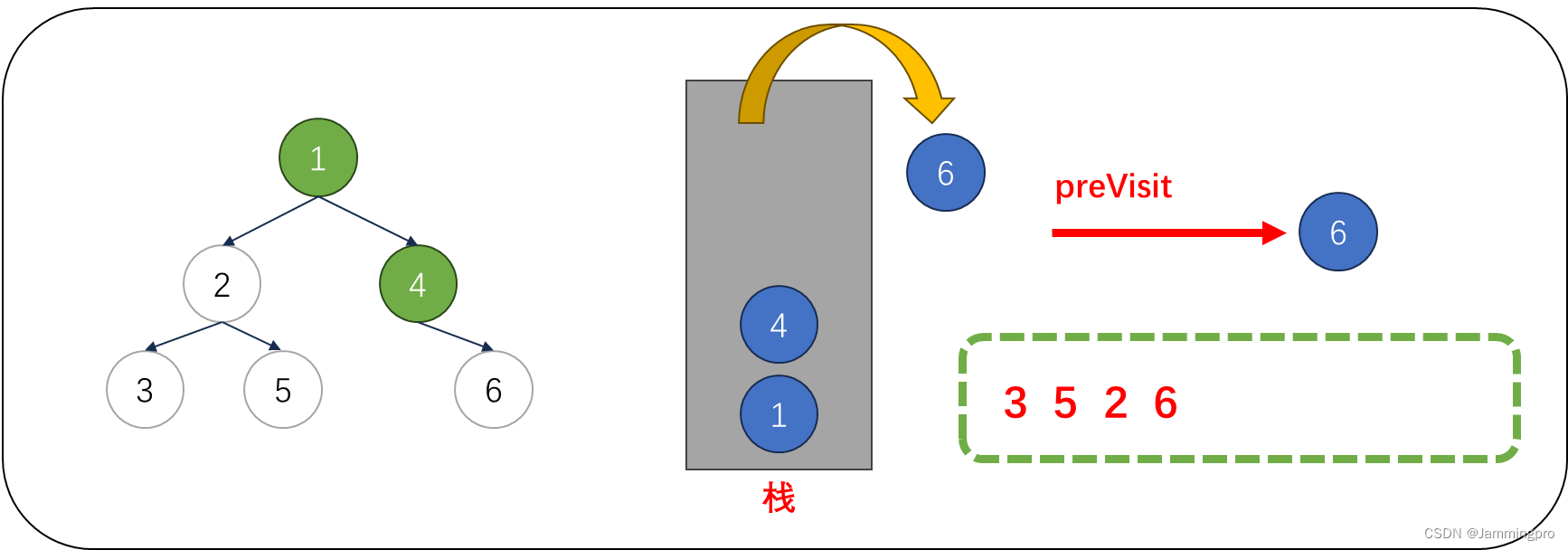
9.此时cur指向值为4的节点，由于cur->right==nullptr || cur->right==preVisit，则表明该结点的右子树已经被访问或为叶子节点，则值为4的节点可以出栈。并将上次访问节点指针preVisit改为值为4的节点。cur指向栈顶元素。

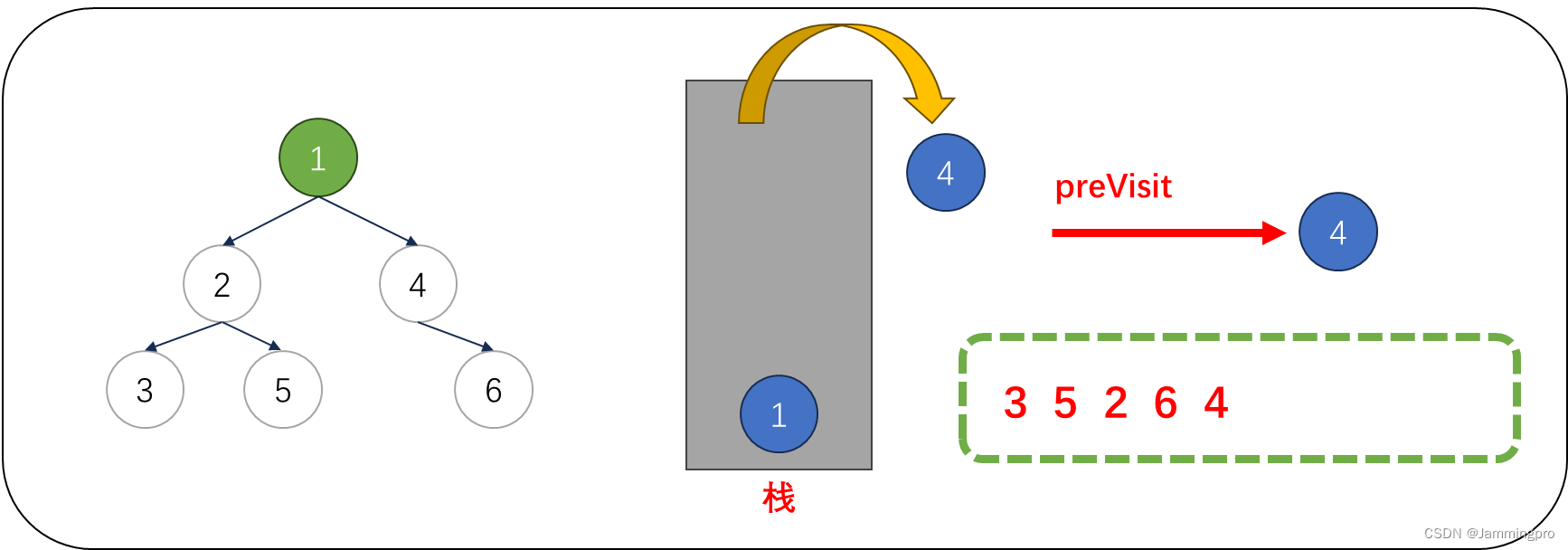
10.此时cur指向值为1的节点，由于cur->right==nullptr || cur->right==preVisit，则表明该结点的右子树已经被访问或为叶子节点，则值为1的节点可以出栈。并将上次访问节点指针preVisit改为值为1的节点。此时需要将cur指向栈顶元素，但由于此时栈为空，则遍历结束。

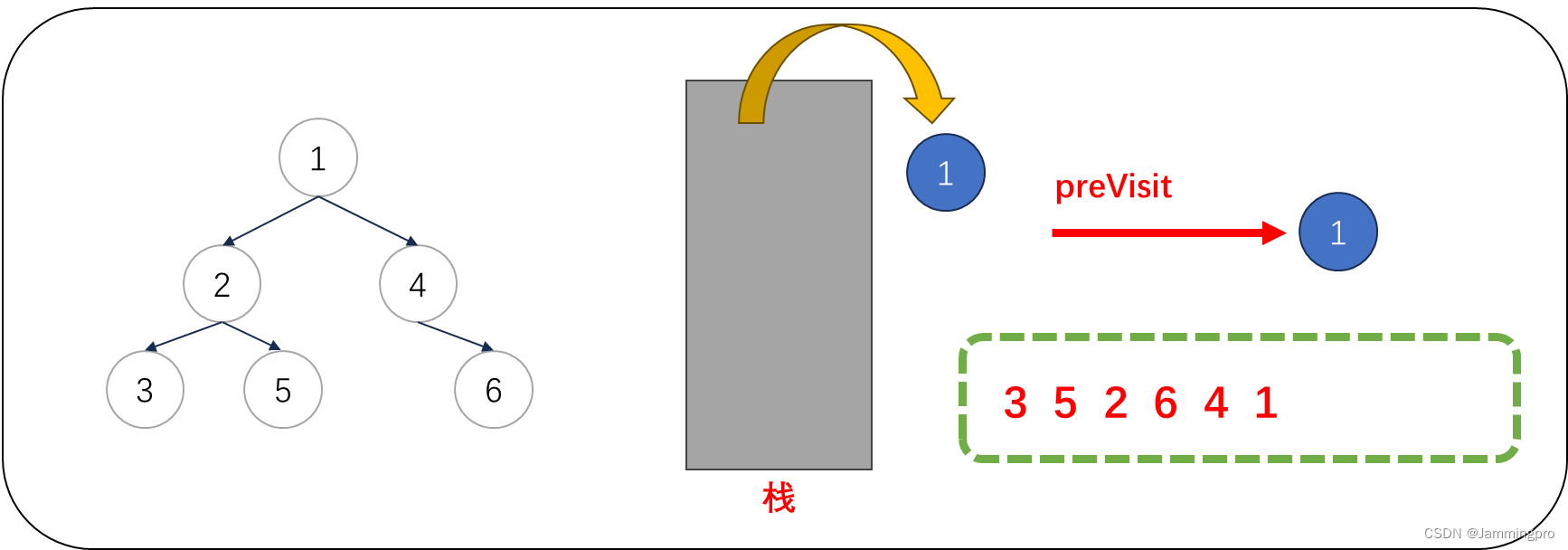
[LeetCode-二叉树的后序遍历]
下面代码给出后序遍历的非递归实现代码↓↓↓

class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        vector<int> ret;
        stack<TreeNode*> stk;
        TreeNode* cur = root;
        TreeNode* preVisit = nullptr;
        while(cur || !stk.empty())
        {
            while(cur)
            {
                stk.push(cur);
                cur = cur->left;
            }
            cur = stk.top();
            if(cur->right == nullptr || cur->right == preVisit)
            {
                ret.push_back(cur->val);
                preVisit = cur;
                cur = nullptr;
                stk.pop();
            }
            else
            {
                cur = cur->right;
            }
        }
        return ret;
    }
};

二叉搜索树

概念

二叉搜索树又称二叉排序树，它或者是一棵空树，或者是具有以下性质的二叉树:

Ⅰ 若它的左子树不为空，则左子树上所有节点的值都小于根节点的值
Ⅱ 若它的右子树不为空，则右子树上所有节点的值都大于根节点的值
Ⅲ 它的左右子树也分别为二叉搜索树

代码实现

查找

由于二叉搜索树的各个节点中，它左子树的值一定小于当前节点的值，右子树的值一定大于当前节点的值。如果我们要搜索的值小于当前节点，则它位于该节点的左树；如果我们要搜索的值大于当前节点，则它位于该节点的右树。

【示例】下面给出一个搜索的例子（搜索的值在二叉搜索树中存在）

当我们要搜索值为6的数据是否存在于该二叉树中时，先使用一个指针cur指向根节点。6大于cur->_val（值为5），则说明要搜索的值位于该节点的右树，则cur=cur->_right。此时6小于cur->_val（值为7），则说明要搜索的值位于该节点的左树，则cur=cur->_left。此时6等于cur->_val（值为6），则说明该树存在值为6节点。

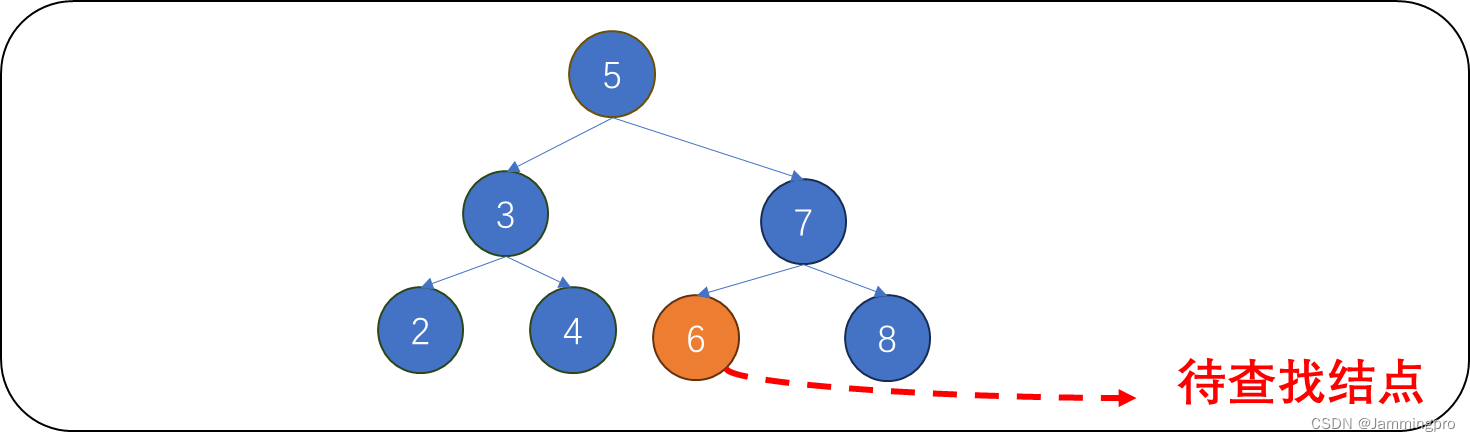
【示例】下面给出待查找结点不在二叉搜索树中的例子

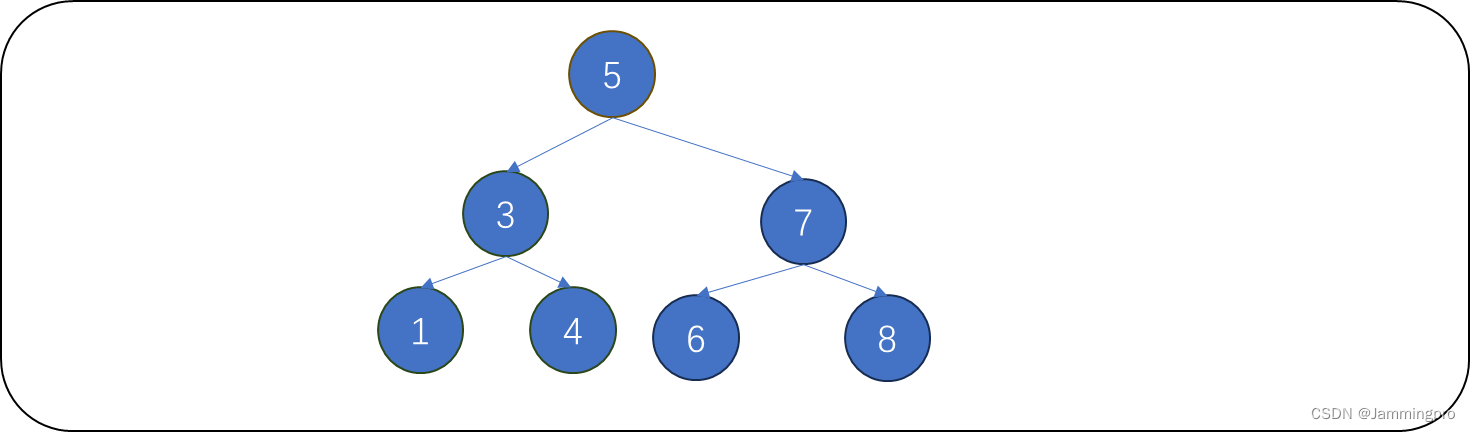
在下图的二叉搜索树中，如果我们要查找值为2的结点。此时当前节点指针cur指向根节点，2小于cur->val（值为5），则该节点为当前节点的左子树，cur=cur->_left。2小于cur->val（值为3），则该节点为当前节点左子树，cur=cur->_left。2大于cur->val（值为1），则待查找节点位于当前节点的右子树，cur=cur->_right，此时cur为空，说明待查找节点并不存在。

下面给出查找代码↓↓↓

bool Find(const K& key)
{
	Node* cur = _root;
	while (cur)
	{
		if (key < cur->_key)
		{
			cur = cur->_left;
		}
		else if (key > cur->_key)
		{
			cur = cur->_right;
		}
		else
		{
			return true;
		}
	}
	return false;
}

插入

在插入新节点的时，如果该节点已经在二叉搜索树中存在了，则拒接插入，返回false。在寻找插入位置时，我们需要使用一个parent指针记录当前节点的双亲结点，cur指向当前结点。使用和查找相同的逻辑思路（比当前结点大，则待插入位置在该结点的右子树；比当前结点小，则待插入位置在该结点的左子树），当cur为空时，parent记录着它的双亲结点，则新插入结点为parent指向结点的孩子。

到底是parent指向结点的左孩子还是有孩子，需要使用判断语句判断：如果待插入值大于parent->_key则插入在它的右子树，否则插入在它的左子树。

下面给出插入代码↓↓↓

bool Insert(const K& key)
{
	if (_root == nullptr)
	{
		_root = new Node(key);
		return true;
	}
	Node* parent = nullptr;
	Node* cur = _root;
	while (cur)
	{
		if (key < cur->_key)
		{
			cur = cur->_left;
		}
		else if (key > cur->_key)
		{
			cur = cur->_right;
		}
		else
		{
			return false;
		}
	}
	cur = new Node(key);
	if (key < parent->_key)
	{
		parent->_left = cur;
	}
	else
	{
		parent->_right = cur;
	}
	return true;
}

删除

删除某个值的前提是：它存在于二叉搜索树中，如果不存在则返回false。在要删除该结点前，我们需要找到该结点并找到它的双亲结点（删除该节点时，需要修改双亲结点的孩子指针）。

但删除某个结点时，要考虑它是否存在孩子结点。可以将删除结点时的情况分为如下几种↓↓↓

情况1：待删除结点不存在任何孩子。
下图中，待删除值为8的结点没有任何孩子，则直接将它的双亲结点（值为7的结点）的右孩子指针修改为空，再释放待删除结点即可。

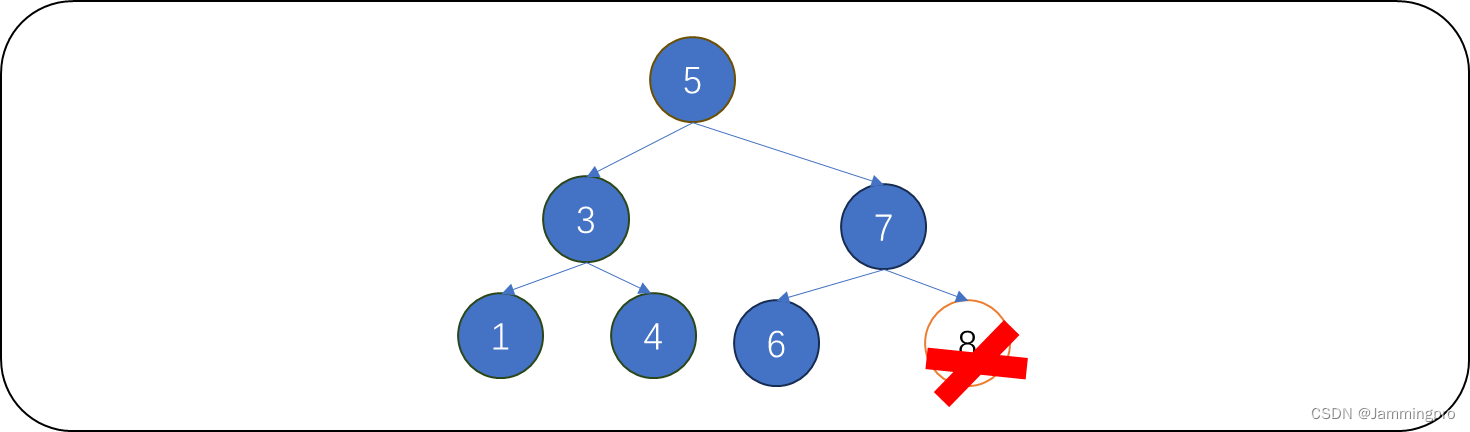
情况2：待删除结点只存在右孩子
下图中，待删除值为7的结点，它只有右孩子，则将它的双亲结点（值为5的结点）原先指向它的指针指向它的右孩子，再释放待删除结点即可。

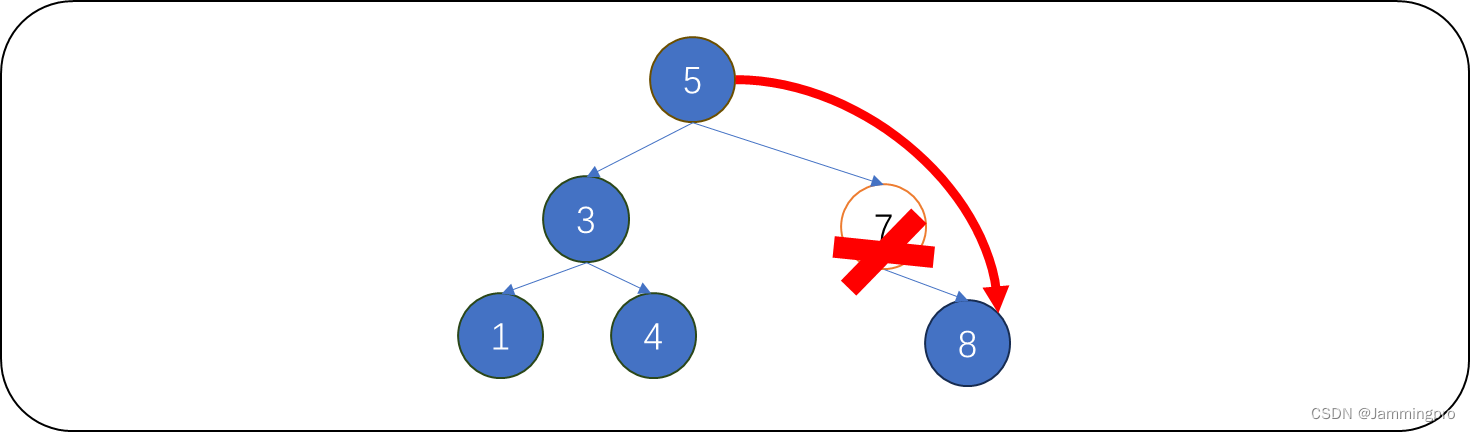
情况3：待删除结点只存在左孩子
下图中，待删除值为7的结点，它只有左孩子，则将它的双亲结点（值为5的结点）原先指向它的指针指向它的左孩子，再释放待删除结点即可。

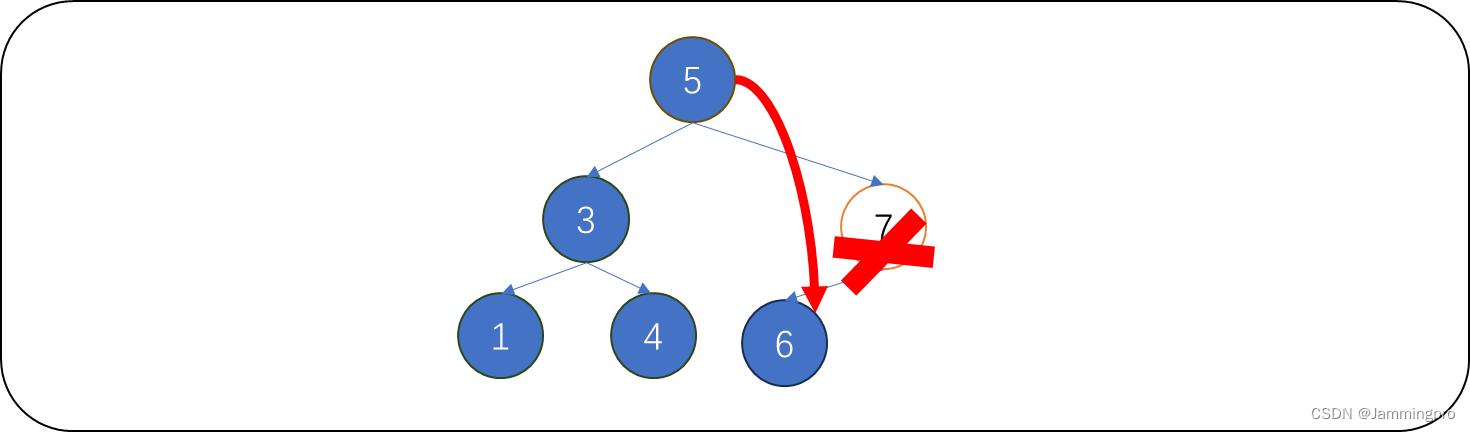
情况4：待删除结点既有左孩子又有右孩子

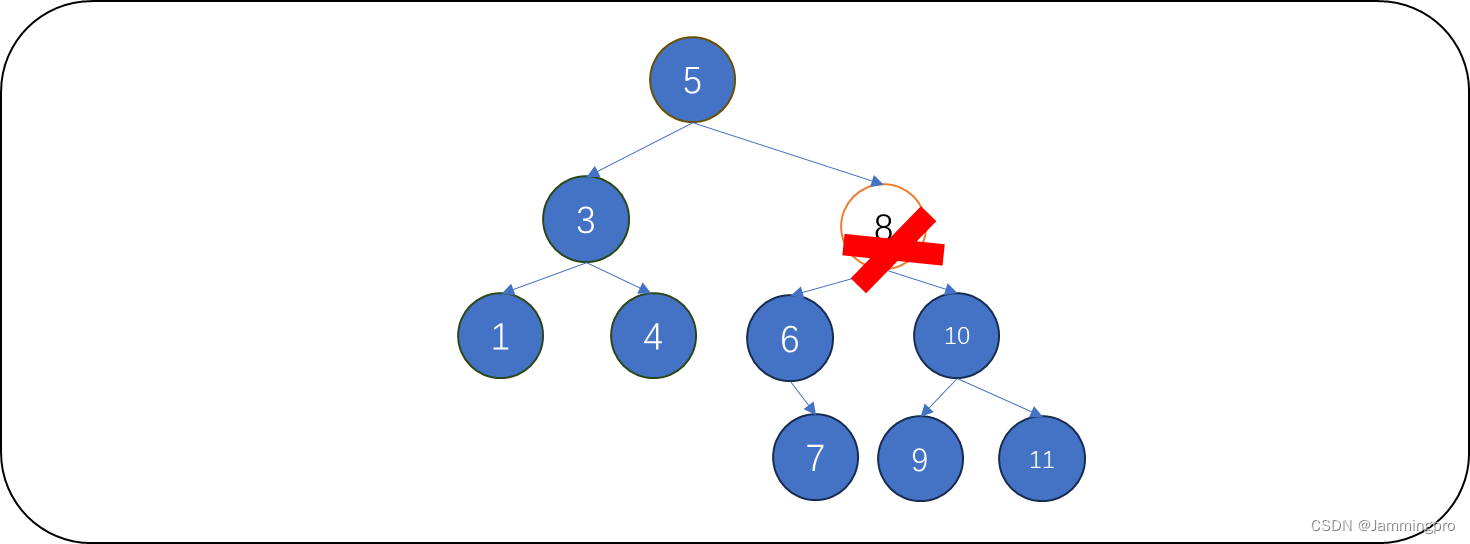
上图中，待删除值为8的结点，它既有左孩子，又有右孩子。此时有两种方式来处理：
处理方式1：从待删除结点的左子树中选择最大结点，将它链到被删除结点的位置上，再释放待删除结点。
ps：从待删除结点的左子树中选择最大值，这个最大值比待删除结点左子树任何值大，比待删除结点右子树任何值小，可以继续保存二叉搜索树结构。

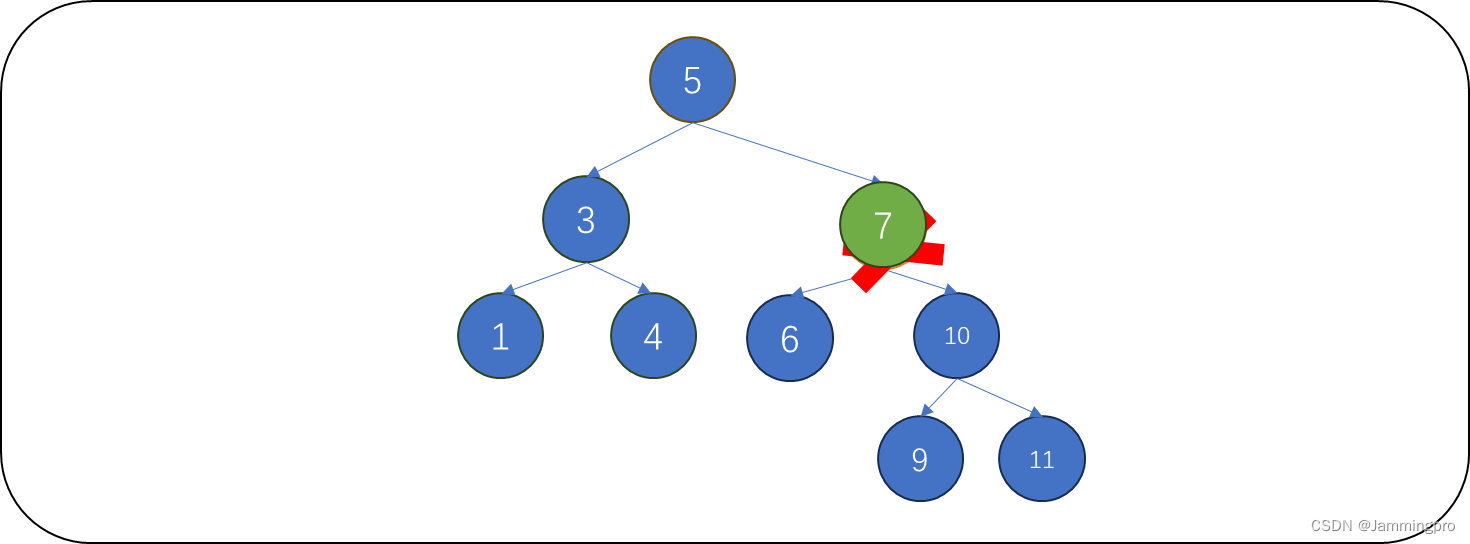
处理方式2：从待删除结点的右子树中选择最小的结点，将它链到被删除结点的位置上，再释放待删除结点。
ps：从待删除结点的右子树中选择最小值，这个值比待删除结点的左子树任何值都大，比待删除结点的右子树任何值都大，可以继续爆出二叉搜索树结构。下面给出的代码采用的是处理方式2。

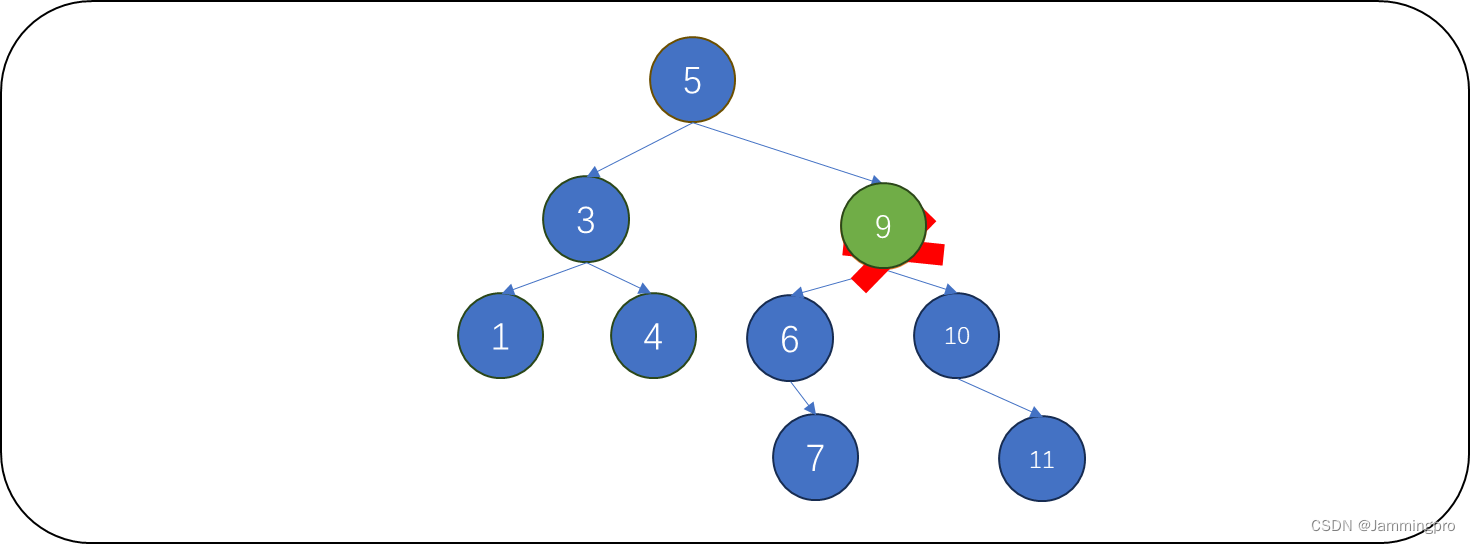
下面给出删除代码↓↓↓

bool Erase(const K& key)
{
	Node* parent = nullptr;
	Node* cur = _root;
	while (cur)
	{
		if (key < cur->_key)
		{
			parent = cur;
			cur = cur->_left;
		}
		else if (key > cur->_key)
		{
			parent = cur;
			cur = cur->_right;
		}
		else
		{
			if (cur->_left == nullptr)
			{
				if (cur == _root)
				{
					_root = cur->_right;
				}
				else
				{
					if (cur = parent->_left)
					{
						parent->_left = cur->_right;
					}
					else
					{
						parent->_right = cur->_right;
					}
				}
				delete cur;
			}
			else if (cur->_right == nullptr)
			{
				if (cur == _root)
				{
					_root = cur->_left;
				}
				else
				{
					if (cur == parent->_left)
					{
						parent->_left = cur->_left;
					}
					else
					{
						parent->_right = cur->_right;
					}
				}
				delete cur;
			}
			else
			{
				Node* minRParent = cur;
				Node* minR = cur->_right;
				while (minR->_left)
				{
					minRParent = minR;
					minR = minR->_left;
				}
				std::swap(minR->_key, cur->_key);
				if (minR == minRParent->_right)
				{
					minRParent->_right = minR->_right;
				}
				else
				{
					minRParent->_left = minR->_right;
				}
				delete minR;
			}
			return true;
		}
	}
	return false;
}

二叉搜索树的完整代码如下↓↓↓

#pragma once

#include <iostream>
using namespace std;

template<class K>
struct BSTreeNode
{
	BSTreeNode* _left = nullptr;
	BSTreeNode* _right = nullptr;
	K _key;

	BSTreeNode(const K& key)
		:_key(key)
	{}
};

template<class K>
class BSTree
{
	typedef BSTreeNode<K> Node;
public:
	bool Find(const K& key)
	{
		Node* cur = _root;
		while (cur)
		{
			if (key < cur->_key)
			{
				cur = cur->_left;
			}
			else if (key > cur->_key)
			{
				cur = cur->_right;
			}
			else
			{
				return true;
			}
		}
		return false;
	}
	bool Insert(const K& key)
	{
		if (_root == nullptr)
		{
			_root = new Node(key);
			return true;
		}
		Node* parent = nullptr;
		Node* cur = _root;
		while (cur)
		{
			if (key < cur->_key)
			{
				parent = cur;
				cur = cur->_left;
			}
			else if (key > cur->_key)
			{
				parent = cur;
				cur = cur->_right;
			}
			else
			{
				return false;
			}
		}
		cur = new Node(key);
		if (key < parent->_key)
		{
			parent->_left = cur;
		}
		else
		{
			parent->_right = cur;
		}
		return true;
	}
	bool Erase(const K& key)
	{
		Node* parent = nullptr;
		Node* cur = _root;
		while (cur)
		{
			if (key < cur->_key)
			{
				parent = cur;
				cur = cur->_left;
			}
			else if (key > cur->_key)
			{
				parent = cur;
				cur = cur->_right;
			}
			else
			{
				if (cur->_left == nullptr)
				{
					if (cur == _root)
					{
						_root = cur->_right;
					}
					else
					{
						if (cur = parent->_left)
						{
							parent->_left = cur->_right;
						}
						else
						{
							parent->_right = cur->_right;
						}
					}
					delete cur;
				}
				else if (cur->_right == nullptr)
				{
					if (cur == _root)
					{
						_root = cur->_left;
					}
					else
					{
						if (cur == parent->_left)
						{
							parent->_left = cur->_left;
						}
						else
						{
							parent->_right = cur->_right;
						}
					}
					delete cur;
				}
				else
				{
					Node* minRParent = cur;
					Node* minR = cur->_right;
					while (minR->_left)
					{
						minRParent = minR;
						minR = minR->_left;
					}
					std::swap(minR->_key, cur->_key);
					if (minR == minRParent->_right)
					{
						minRParent->_right = minR->_right;
					}
					else
					{
						minRParent->_left = minR->_right;
					}
					delete minR;
				}
				return true;
			}
		}
		return false;
	}
	void InOrder()
	{
		_InOrder(_root);
		cout << endl;
	}
private:
	void _InOrder(Node* node)
	{
		if (node == nullptr)return;
		_InOrder(node->_left);
		cout << node->_key << " ";
		_InOrder(node->_right);
	}
private:
	Node* _root = nullptr;
};

应用

K模型

K模型即只有key作为关键码，结构中只需要存储Key即可，关键码即为需要搜索到的值。

【示例】给一个单词word，判断该单词是否拼写正确

以词库中所有单词集合中的每个单词作为key，构建一棵二叉搜索树。在二叉搜索树中检索该单词是否存在，存在则拼写正确，不存在则拼写错误。下面代码中演示了该功能，使用色二叉搜索树为上方实现的代码（以BSTree.hpp引入）↓↓↓

#include <iostream>
#include <string.h>
#include "BSTree.hpp"
using namespace std;

void test()
{
	BSTree<string> t;
	//这里仅导入部分英文单词
	t.Insert("apple");
	t.Insert("banana");
	t.Insert("orange");
	t.Insert("fish");
	t.Insert("pig");

	string s;
	cin >> s;

	if (t.Find(s))
	{
		cout << "拼写正确" << endl;
	}
	else
	{
		cout << "拼写错误" << endl;
	}
}

int main()
{
	test();
}

KV模型

每一个关键码key，都有与之对应的值Value，即<Key, Value>的键值对。在二叉搜索树中以key值来作为查找的依据，通过找到key值后，获取它的value。

我们将上述搜索二叉树改为kv存储。↓↓↓（ps：下方代码设置右值引用返回）

#pragma once

#include <iostream>
using namespace std;

template<class K, class V>
struct MyPair
{
	K _k;
	V _v;
	MyPair(const K& k = K(), const V& v = V())
		:_k(k)
		,_v(v)
	{}
	bool operator!=(const MyPair<K, V>& obj)
	{
		return _k != obj._k;
	}
};

template<class K, class V>
struct BSTreeNode
{
	BSTreeNode* _left = nullptr;
	BSTreeNode* _right = nullptr;
	MyPair<K, V> _kv;

	BSTreeNode(const K& key, const V& val)
		:_kv(MyPair<K, V>(key, val))
	{}
};

template<class K, class V>
class BSTree
{
	typedef BSTreeNode<K, V> Node;
public:
	MyPair<K, V>&& Find(const K& key)
	{
		Node* cur = _root;
		while (cur)
		{
			if (key < cur->_kv._k)
			{
				cur = cur->_left;
			}
			else if (key > cur->_kv._k)
			{
				cur = cur->_right;
			}
			else
			{
				return move(cur->_kv);
			}
		}
		return MyPair<K, V>();
	}
	bool Insert(const K& key, const V& val)
	{
		if (_root == nullptr)
		{
			_root = new Node(key, val);
			return true;
		}
		Node* parent = nullptr;
		Node* cur = _root;
		while (cur)
		{
			if (key < cur->_kv._k)
			{
				parent = cur;
				cur = cur->_left;
			}
			else if (key > cur->_kv._k)
			{
				parent = cur;
				cur = cur->_right;
			}
			else
			{
				return false;
			}
		}
		cur = new Node(key, val);
		if (key < parent->_kv._k)
		{
			parent->_left = cur;
		}
		else
		{
			parent->_right = cur;
		}
		return true;
	}
	bool Erase(const K& key)
	{
		Node* parent = nullptr;
		Node* cur = _root;
		while (cur)
		{
			if (key < cur->_kv._k)
			{
				parent = cur;
				cur = cur->_left;
			}
			else if (key > cur->_kv._k)
			{
				parent = cur;
				cur = cur->_right;
			}
			else
			{
				if (cur->_left == nullptr)
				{
					if (cur == _root)
					{
						_root = cur->_right;
					}
					else
					{
						if (cur = parent->_left)
						{
							parent->_left = cur->_right;
						}
						else
						{
							parent->_right = cur->_right;
						}
					}
					delete cur;
				}
				else if (cur->_right == nullptr)
				{
					if (cur == _root)
					{
						_root = cur->_left;
					}
					else
					{
						if (cur == parent->_left)
						{
							parent->_left = cur->_left;
						}
						else
						{
							parent->_right = cur->_right;
						}
					}
					delete cur;
				}
				else
				{
					Node* minRParent = cur;
					Node* minR = cur->_right;
					while (minR->_left)
					{
						minRParent = minR;
						minR = minR->_left;
					}
					std::swap(minR->_kv, cur->_kv);
					if (minR == minRParent->_right)
					{
						minRParent->_right = minR->_right;
					}
					else
					{
						minRParent->_left = minR->_right;
					}
					delete minR;
				}
				return true;
			}
		}
		return false;
	}
	void InOrder()
	{
		_InOrder(_root);
		cout << endl;
	}
private:
	void _InOrder(Node* node)
	{
		if (node == nullptr)return;
		_InOrder(node->_left);
		cout << node->_kv._k << "|" << node->_kv._v << endl;
		_InOrder(node->_right);
	}
private:
	Node* _root = nullptr;
};

【示例】使用上述修改的KV型二叉搜索树，统计用户输入的各个单词的次数↓↓↓

void test()
{
	BSTree<string, int> t;
	string s;
	while (std::getline(std::cin, s))
	{
		MyPair<string, int>&& ret = t.Find(s);
		if (ret != MyPair<string, int>())
		{
			ret._v++;
		}
		else
		{
			t.Insert(s, 1);
		}
	}
	t.InOrder();
}

性能分析

插入和删除操作都必须先查找，查找效率代表了二叉搜索树中各个操作的性能。

而二叉搜索树的最大搜索次数与二叉树的高度有关，如果搜索二叉搜索树的高度越高则搜索时需要的结点跳转次数越多。而二叉树搜索树的结构与插入的顺序有关，例如我们插入2到8这7个数，如果以5、4、3、2、6、7、8，则它插入后的结构如下图左侧所示，它是一颗完全二叉树；而如果以2、3、4、5、6、7、8的顺序插入，则整个结构将退化为链表（如下图右侧所示）。

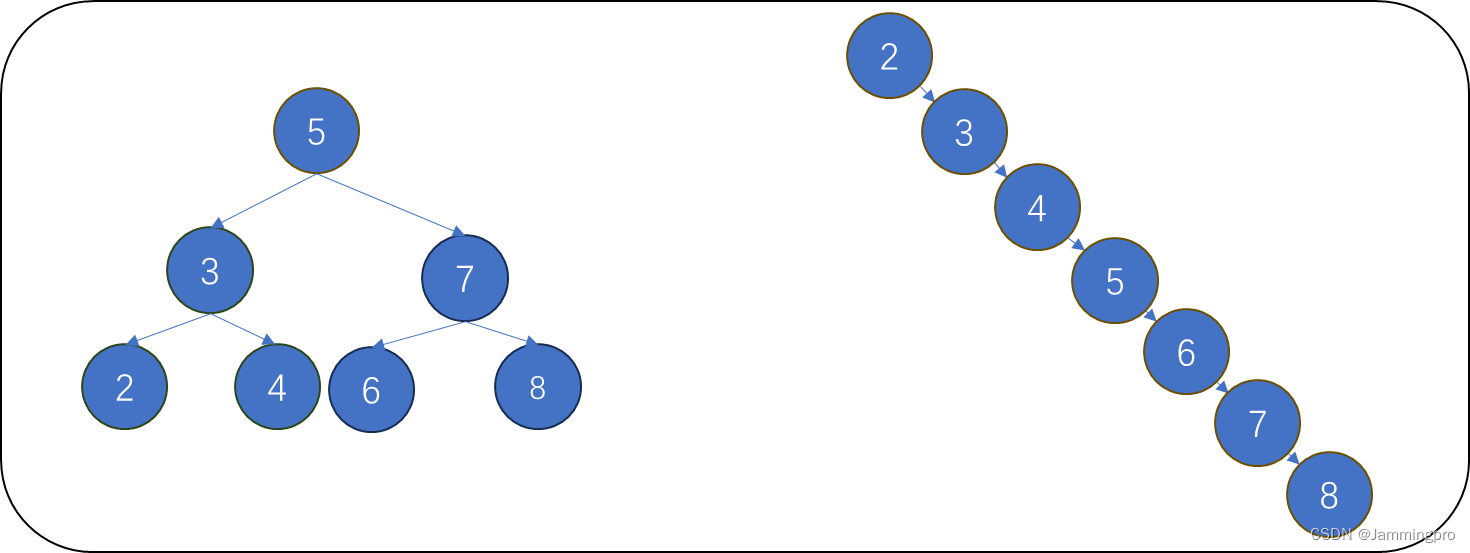
因此，二叉搜索树最好的情况下，它的效率为$O(lo{g}_{2}N)$。最差的情况下，它的效率与链表相同，即$O(N)$.

如果退化成单支树，二叉搜索树的性能就失去了。那能否进行改进，不论按照什么次序插入关键码，二叉搜索树的性能都能达到最优呢？那就需要使用二叉平衡搜索树与红黑树了，这两个内容将在后序完整介绍。

🎈欢迎进入Super数据结构专栏，查看更多文章。
如果上述内容有任何问题，欢迎在下方留言区指正b(￣▽￣)d