二叉查找树、二叉搜索树、二叉排序树算法分析及实现

news2024/10/7 19:20:51

一、几个概念

二叉树（Binary Tree），是 n（n >= 0）个结点（每个结点最多只有2棵子树）的有限集合，该集合或为空集，称为空二叉树，或由一个根节点和两颗互不相交的，称为根节点的左子树和右子树组成，且其左右子树也分别是一颗二叉树。

二叉查找树（Binary Search Tree，简称 BST），又称为二叉搜索树、有序二叉树（Ordered Binary Tree）。二叉查找树或是空二叉树，或是满足以下三个性质的二叉树。

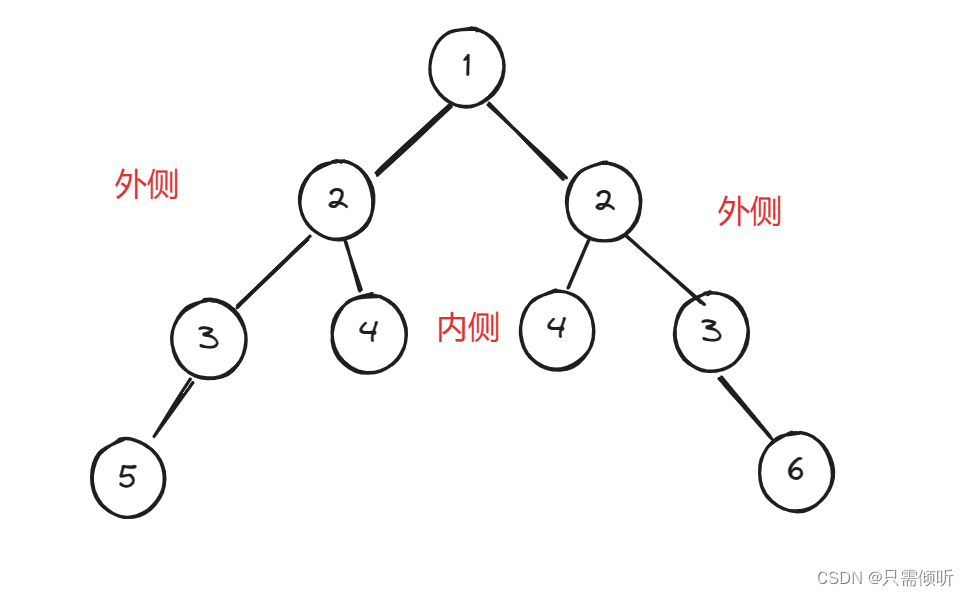
  • 若其左子树非空，则左子树上所有节点的值都小于根节点的值
  • 若其右子树非空，则右子树上所有节点的值都大于根节点的值
  • 其左右子树也分别是一棵二叉查找树

前序遍历二叉树（Pre-order Traversal）：从根结点出发，先访问该结点，然后前序遍历该结点的左子树，再然后前序遍历该结点的右子树

中序遍历二叉树（In-order Traversal）的规则为：从根结点出发，先中序遍历该结点的左子树，然后访问该结点，再然后中序遍历该结点的右子树

后序遍历二叉树（Post-order Traversal）的规则为：从根结点出发，先后序遍历该结点的左子树，然后后序遍历该结点的右子树，再然后访问该结点

二叉链表：是二叉树的一种链式存储结构，其中每个结点包含三个字段：一个数据字段(data)和两个指针字段(*lchild、*rchild)，分别指向该结点的左孩子和右孩子。如果某个结点没有左孩子或右孩子，那么对应的指针字段为NULL。

用 C 语言可以表述为：

typedef struct BST_node {
    int data;
    struct BST_node *lchild, *rchild;
}*BST;

二、二叉查找树的特性

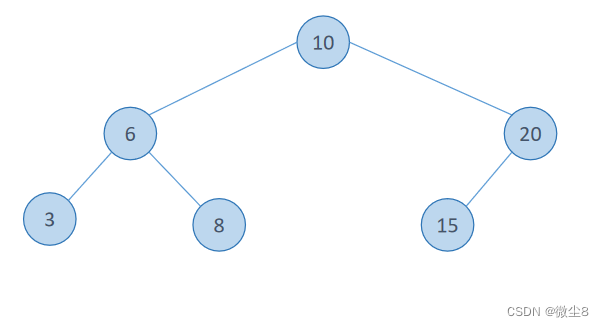
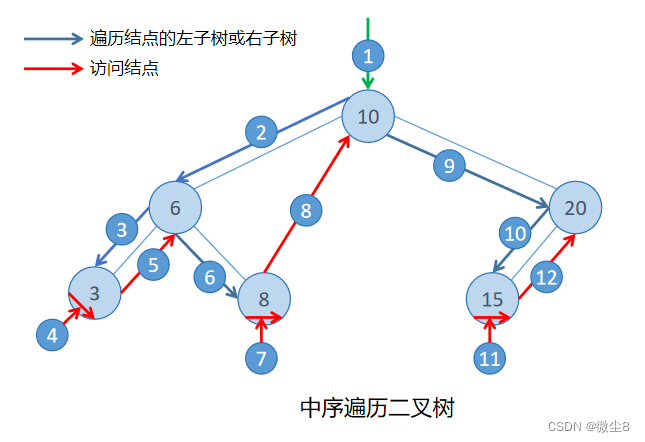
通过中序遍历二叉查找树，得到的序列是有序的递增序列

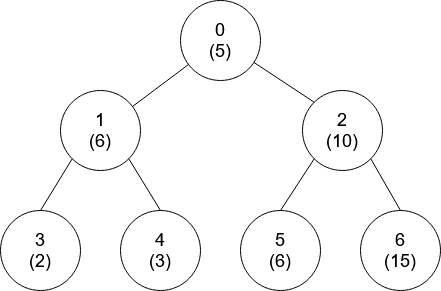
如下图所示的一颗二叉查找树，其中序遍历的序列为：{3,6,8,10,15,20}

三、二叉查找树的查找

因为通过中序遍历二叉查找树，得到的序列是有序的递增序列，因此二叉查找树的查找跟二分查找法类似。

假设有一棵二叉查找树：T，每个结点有数据字段（data），有两个指针字段(*lchild、*rchild)，分别指向结点的左孩子和右孩子。查找 data，如果找到则返回该结点，否则返回 NULL

1、算法思路

  • 如果二叉查找树为空树，则查找失败，返回 NULL
  • 如果二叉查找树不为空

（1）如果 T->data == data，则返回该结点

（2）如果 T->data > data，则递归查找左子树

（3）如果 T->data < data，则递归查找右子树

时间复杂度

  • 最好的情况，根结点就是要查找的结点，所以最好时间复杂度为： O(1)
  • 最差的情况，二叉查找树退化为链表时，所以最差时间复杂度为： O(n)
  • 平均时间复杂度为：O(\log n)

2、实现代码

#include <stdio.h>
#include <stdlib.h>

// 扩展二叉树前序序列
char *g_bad_str = "7654321########";
char *g_average_str = "421##3##65##7##";
int g_index = 0;
char *g_str = NULL;
int g_search_times = 0;

typedef enum BST_TYPE {
    BAD,
    AVERAGE
}BST_TYPE;

typedef struct BST_node {
    int data;
    struct BST_node *lchild, *rchild;
}*BST;

// 二叉查找树查找
BST bst_search(BST const T, const char data) {
    if (!T)
        return NULL;
    
    g_search_times++;
    if (T->data == data)
        return T;
    else if (T->data > data)
        return bst_search(T->lchild, data);
    else
        return bst_search(T->rchild, data);
}

void bst_create(BST *T, BST_TYPE type) {
    if (type == BAD)
        g_str = g_bad_str;
    else
        g_str = g_average_str;
    
    if (g_str[g_index] == '#') {
        *T = NULL;
        g_index++;
    } else {
        *T = malloc(sizeof(**T));
        (*T)->data = g_str[g_index];
        (*T)->lchild = NULL;
        (*T)->rchild = NULL;
        g_index++;
        bst_create(&(*T)->lchild, type);
        bst_create(&(*T)->rchild, type);
    }
}

void bst_destroy(BST T) {
    if (!T)
        return;
    
    bst_destroy(T->lchild);
    bst_destroy(T->rchild);
    printf("free %c\n", T->data);
    free(T);
}

int main(int argc, char *argv[]) {
    BST tree_bad = NULL;
    BST tree_average = NULL;
    BST tree_search = NULL;
    
    g_index = 0;
    bst_create(&tree_bad, BAD);

    g_index = 0;
    bst_create(&tree_average, AVERAGE);

    g_search_times = 0;
    char data = '1';
    tree_search = bst_search(tree_bad, data);
    if (tree_search)
        printf("bad search_times = %d, data = %c\n", g_search_times, tree_search->data);
    else
        printf("can't find %c, bad search_times = %d\n", data, g_search_times);

    g_search_times = 0;
    data = '7';
    tree_search = bst_search(tree_average, data);
    if (tree_search)
        printf("average search_times = %d, data = %c\n", g_search_times, tree_search->data);
    else 
        printf("can't find %c, average search_times = %d\n", data, g_search_times);

    printf("----------\n");
    bst_destroy(tree_bad);
    printf("----------\n");
    bst_destroy(tree_average);

    return 0;
}

四、二叉查找树的插入

因为通过中序遍历二叉查找树，得到的序列是有序的递增序列，因此二叉查找树的插入跟二分插入法类似。

假设有一个二叉查找树指针：T，每个结点有数据字段（data），有两个指针字段(*lchild、*rchild)，分别指向结点的左孩子和右孩子，并将数据 data 插入到其中。

1、算法思路

（1）如果二叉查找树指针 T 为 NULL，则创建新结点，并插入到当前位置

（2）如果 T->data > data，则递归插入到左子树中

（3）如果 T->data <= data，则递归插入到右子树中

时间复杂度

  • 最好的情况，根结点为空时，所以最好时间复杂度为： O(1)
  • 最差的情况，二叉查找树退化为链表时，所以最差时间复杂度为： O(n)
  • 平均时间复杂度为：O(\log n)

2、实现代码

#include <stdio.h>
#include <stdlib.h>

int g_insert_times = 0;

typedef struct BST_node {
    int data;
    struct BST_node *lchild, *rchild;
}*BST;

// 二叉查找树插入
void bst_insert(BST *T, int data) {
    g_insert_times++;
    if (!(*T)) {
        *T = malloc(sizeof(**T));
        (*T)->data = data;
        (*T)->lchild = NULL;
        (*T)->rchild = NULL;
        printf("insert %c success, insert times = %d\n", data, g_insert_times);
    } else if ((*T)->data > data) {
        bst_insert(&(*T)->lchild, data);
    } else {
        bst_insert(&(*T)->rchild, data);
    }
}

void bst_destroy(BST T) {
    if (!T)
        return;
    
    bst_destroy(T->lchild);
    bst_destroy(T->rchild);
    printf("free %c\n", T->data);
    free(T);
}

void visit_node(BST T) {
    printf("%c\n", T->data);
}

void in_order_tree(BST T) {
    if (!T)
        return;

    in_order_tree(T->lchild);
    visit_node(T);
    in_order_tree(T->rchild);
}

void bst_test(BST *T) {
    g_insert_times = 0;
    bst_insert(T, '4');
    g_insert_times = 0;
    bst_insert(T, '2');
    g_insert_times = 0;
    bst_insert(T, '6');
    g_insert_times = 0;
    bst_insert(T, '1');
    g_insert_times = 0;
    bst_insert(T, '5');
    g_insert_times = 0;
    bst_insert(T, '3');
    g_insert_times = 0;
    bst_insert(T, '7');
}

void bst_test1(BST *T) {
    g_insert_times = 0;
    bst_insert(T, '7');
    g_insert_times = 0;
    bst_insert(T, '6');
    g_insert_times = 0;
    bst_insert(T, '5');
    g_insert_times = 0;
    bst_insert(T, '4');
    g_insert_times = 0;
    bst_insert(T, '3');
    g_insert_times = 0;
    bst_insert(T, '2');
    g_insert_times = 0;
    bst_insert(T, '1');
}

int main(int argc, char *argv[]) {
    BST T = NULL;
    BST T1 = NULL;

    bst_test(&T);
    printf("-------------\n");
    bst_test1(&T1);
    printf("---------\n");
    bst_destroy(T);
    printf("---------\n");
    bst_destroy(T1);

    return 0;
}

五、二叉查找树的删除

1、算法思路

（1）如果被删除结点的左子树为空时，将该结点的父结点中，让指向该结点的指针域指向该结点的右子树，然后删除该结点

（2）如果被删除结点的右子树为空时，将该结点的父结点中，让指向该结点的指针域指向该结点的左子树，然后删除该结点

（3）如果被删除结点的左右子树都不为空时，情况复杂的多，因为父结点的左指针或右指针不能同时指向被删除结点的左右子树。我们可以采用

  • 合并删除法

合并删除法：将被删除结点的左右子树合并得到一棵树，然后把这棵树挂到被删除结点的父结点中。

如何将被删除结点的左右子树合并得到一棵树呢？

因为二叉查找树的特性是：左子树的每个结点的值都比右子树每个结点的值小，所以，可以把被删除结点的左子树中值最大的结点（左子树中，沿着右结点找，结点的右指针为空的结点）作为被删除结点的右子树的父结点 或 被删除结点的右子树中，值最小的结点（右子树中，沿着左结点找，结点的左指针为空的结点）作为被删除结点的左子树的父结点，从而合并得到一棵树，然后挂到被删除结点的父结点中。

时间复杂度

  • 最好的情况，被删除的结点是根结点，且二叉查找树退化为链表时，此时查找的时间复杂度为 O(1)，删除的时间复杂度为 O(1)，所以最好时间复杂度为： O(1)
  • 最差的情况，二叉查找树退化为链表时，此时查找的时间复杂度为 O(n)，删除的时间复杂度为 O(1)，所以最差时间复杂度为： O(n)
  • 平均时间复杂度为：O(\log n)

2、代码实现

#include <stdio.h>
#include <stdlib.h>

typedef struct BST_node {
    int data;
    struct BST_node *lchild, *rchild;
}*BST;

// 二叉查找树查找
BST* bst_search(BST* const T, int data) {
    if (!(*T))
        return NULL;
    
    if ((*T)->data == data)
        return T;
    else if ((*T)->data > data)
        return bst_search(&(*T)->lchild, data);
    else 
        return bst_search(&(*T)->rchild, data);
}

// 二叉查找树插入
void bst_insert(BST *T, int data) {
    if (!(*T)) {
        *T = malloc(sizeof(**T));
        (*T)->data = data;
        (*T)->lchild = NULL;
        (*T)->rchild = NULL;
    } else if ((*T)->data > data) {
        bst_insert(&(*T)->lchild, data);
    } else {
        bst_insert(&(*T)->rchild, data);
    }
}

void bst_destroy(BST T) {
    if (!T)
        return;
    
    bst_destroy(T->lchild);
    bst_destroy(T->rchild);
    free(T);
}

void visit_node(BST T) {
    printf("%d\n", T->data);
}

void in_order_tree(BST T) {
    if (!T)
        return;

    in_order_tree(T->lchild);
    visit_node(T);
    in_order_tree(T->rchild);
}

void bst_create1(BST *T) {
    // 2346
    bst_insert(T, 4);
    bst_insert(T, 2);
    bst_insert(T, 6);
    bst_insert(T, 3);

    in_order_tree(*T);
    printf("----------\n");
}

void bst_create2(BST *T) {
    // 1246
    bst_insert(T, 4);
    bst_insert(T, 2);
    bst_insert(T, 6);
    bst_insert(T, 1);

    in_order_tree(*T);
    printf("----------\n");
}

void bst_create3(BST *T) {
    // 12345678
    bst_insert(T, 7);
    bst_insert(T, 4);
    bst_insert(T, 8);
    bst_insert(T, 2);
    bst_insert(T, 6);
    bst_insert(T, 1);
    bst_insert(T, 3);
    bst_insert(T, 5);

    in_order_tree(*T);
    printf("----------\n");
}

void bst_delete_by_merge(BST *T, int data) {
    BST* del_node = bst_search(T, data);
    if (!(*del_node))
        return;
    
    BST tmp = (*del_node);

    if (!(*del_node)->lchild) // 左孩子为空
        *del_node = (*del_node)->rchild;
    else if (!(*del_node)->rchild) // 右孩子为空
        *del_node = (*del_node)->lchild;
    else { // 左右子树都不为空
        // 把被删除结点左子树中值最大的结点（左子树中，沿着右结点找，结点的右指针为空的结点）作为被删除右子树的父结点
        BST rmax = (*del_node)->lchild;
        while(rmax->rchild) {
            rmax = rmax->rchild;
        }
        rmax->rchild = (*del_node)->rchild;

        // 挂到被删除结点的父结点中
        *del_node = (*del_node)->lchild;
    }

    printf("delete %d success\n", tmp->data);
    free(tmp);
}

int main(int argc, char *argv[]) {
    BST T1 = NULL;
    BST T2 = NULL;
    BST T3 = NULL;

    bst_create1(&T1);
    bst_delete_by_merge(&T1, 2);
    in_order_tree(T1);
    printf("--------\n");

    bst_create2(&T2);
    bst_delete_by_merge(&T2, 2);
    in_order_tree(T2);
    printf("--------\n");

    bst_create3(&T3);
    bst_delete_by_merge(&T3, 4);
    in_order_tree(T3);
    printf("--------\n");


    bst_destroy(T1);
    bst_destroy(T2);
    bst_destroy(T3);

    return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1589561.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

算法练习第16天|101. 对称二叉树

算法练习第16天|101. 对称二叉树

101. 对称二叉树 力扣链接https://leetcode.cn/problems/symmetric-tree/description/ 题目描述&#xff1a; 给你一个二叉树的根节点 root &#xff0c; 检查它是否轴对称。 示例 1&#xff1a; 输入&#xff1a;root [1,2,2,3,4,4,3] 输出&#xff1a;true示例 2&#x…
阅读更多...
稀碎从零算法笔记Day46-LeetCode:互质树

稀碎从零算法笔记Day46-LeetCode:互质树

这几天有点懈怠了 题型&#xff1a;树、DFS、BSF、数学 链接&#xff1a;1766. 互质树 - 力扣&#xff08;LeetCode&#xff09; 来源&#xff1a;LeetCode 题目描述 给你一个 n 个节点的树&#xff08;也就是一个无环连通无向图&#xff09;&#xff0c;节点编号从 0 到 …
阅读更多...
力扣207.课程表

力扣207.课程表

你这个学期必须选修 numCourses 门课程&#xff0c;记为 0 到 numCourses - 1 。 在选修某些课程之前需要一些先修课程。 先修课程按数组 prerequisites 给出&#xff0c;其中 prerequisites[i] [ai, bi] &#xff0c;表示如果要学习课程 ai 则 必须 先学习课程 bi 。 例如…
阅读更多...
2024-3-29 群讨论：如何看到一个线程的所有 JFR 事件

2024-3-29 群讨论：如何看到一个线程的所有 JFR 事件

以下来自本人拉的一个关于 Java 技术的讨论群。关注公众号&#xff1a;hashcon&#xff0c;私信拉你 如何查看一个线程所有相关的 JFR 事件 一般接口响应慢&#xff0c;通过日志可以知道是哪个线程&#xff0c;但是如何查看这个线程的所有相关的 JFR 事件呢&#xff1f;JMC 有…
阅读更多...
77、WAF攻防——权限控制代码免杀异或运算变量覆盖混淆加密传参

77、WAF攻防——权限控制代码免杀异或运算变量覆盖混淆加密传参

文章目录 WAF规则webshell免杀变异 WAF规则 函数匹配 工具指纹 webshell免杀变异 php 传参带入 eval可以用assert来替换,assert也可以将字符串当作php代码执行漏洞 php 变量覆盖 php 加密 使用加密算法对php后门进行加密 php 异或运算 简化:无字符webshellP 无数字字母rc…
阅读更多...
WPS二次开发系列：Gradle版本、AGP插件与Java版本的对应关系

WPS二次开发系列：Gradle版本、AGP插件与Java版本的对应关系

背景 最近有体验SDK的同学反馈接入SDK出现报错&#xff0c;最终定位到原因为接入的宿主app项目的gradle版本过低导致&#xff0c;SDK兼容支持了android11的特性&#xff0c;需要对应的gradle插件为支持android11的版本。 现象 解决方案 将gradle版本升级至支持android11的插件版…
阅读更多...
【数据结构与算法】之8道顺序表与链表典型编程题心决！

【数据结构与算法】之8道顺序表与链表典型编程题心决！

个人主页&#xff1a;秋风起&#xff0c;再归来~ 数据结构与算法 个人格言&#xff1a;悟已往之不谏&#xff0c;知来者犹可追 克心守己&#xff0c;律己则安&#xff01; 目录 1、顺序表 1.1 合并两个有序数组 1.2 原地移除数组中所有的元素va…
阅读更多...
Python+selenium搭建Web自动化测试框架

Python+selenium搭建Web自动化测试框架

&#x1f345; 视频学习&#xff1a;文末有免费的配套视频可观看 &#x1f345; 点击文末小卡片&#xff0c;免费获取软件测试全套资料&#xff0c;资料在手&#xff0c;涨薪更快 在程序员的世界中&#xff0c;一切重复性的工作&#xff0c;都应该通过程序自动执行。「自动化测…
阅读更多...
Uniapp+基于百度智能云完成AI视觉功能（附前端思路）

Uniapp+基于百度智能云完成AI视觉功能（附前端思路）

本博客使用uniapp百度智能云图像大模型中的AI视觉API&#xff08;本文以物体检测为例&#xff09;完成了一个简单的图像识别页面&#xff0c;调用百度智能云API可以实现快速训练模型并且部署的效果。 uniapp百度智能云AI视觉页面实现 先上效果图实现过程百度智能云Easy DL训练图…
阅读更多...
Proxmox VE qm 方式一键创建Windows虚拟机

Proxmox VE qm 方式一键创建Windows虚拟机

前言 实现qm 方式一键创建Windows虚拟机&#xff0c;提高效率。 qm 一键创建Windows虚拟机 以下实现在线下载镜像&#xff0c;创建虚拟机&#xff0c;安装系统需要自己手动安装哦&#xff0c;如果想实现全自动安装系统&#xff0c;建议部署自己的内网pxe server 系统参考各参…
阅读更多...
蓝桥杯——松散子序列

蓝桥杯——松散子序列

题目 分析 很明显的动态规划问题&#xff0c;每次我们都取当前位置的最大值就可&#xff0c;从头开始&#xff0c;dp[i]max(dp[i-2],dp[i-3])num[i-3]. 代码 ninput() num[] for i in n:num.append(ord(i)-96) dp[0]*(len(num)3) for i in range(3,len(num)3):dp[i]max(dp[i…
阅读更多...
基于特征的多模态生物信号信息检索与自相似矩阵:专注于自动分割

基于特征的多模态生物信号信息检索与自相似矩阵:专注于自动分割

论文地址&#xff1a;Biosensors | Free Full-Text | Feature-Based Information Retrieval of Multimodal Biosignals with a Self-Similarity Matrix: Focus on Automatic Segmentation (mdpi.com) 论文源码&#xff1a;无 期刊&#xff1a;biosensors 这篇论文提出了一种基…
阅读更多...
java数据结构与算法刷题-----LeetCode172. 阶乘后的零

java数据结构与算法刷题-----LeetCode172. 阶乘后的零

java数据结构与算法刷题目录&#xff08;剑指Offer、LeetCode、ACM&#xff09;-----主目录-----持续更新(进不去说明我没写完)&#xff1a;https://blog.csdn.net/grd_java/article/details/123063846 文章目录 数学&#xff1a;阶乘的10因子个数数学优化:思路转变为求5的倍数…
阅读更多...
JQuery ajax请求

JQuery ajax请求

实现卡号绑定功能 通过 jQuery ajax 请求用户列表数据。 API 接口地址 卡号列表 js/cardnolist.json 接口响应示例 补全 index.js 中空缺代码&#xff0c;实现用户输入完卡号与密码后&#xff0c;与 ajax 请求到的卡号数据进行比对&#xff0c;当卡号和密码匹配成功时&a…
阅读更多...
使用 Docker 部署 Linux-Command 命令搜索工具

使用 Docker 部署 Linux-Command 命令搜索工具

1&#xff09;介绍 Linux-Command GitHub&#xff1a;https://github.com/jaywcjlove/linux-command Linux-Command 仓库搜集了 580 多个 Linux 命令&#xff0c;是一个非盈利性的仓库&#xff0c;生成了一个 Web 网站方便使用&#xff0c;目前网站没有任何广告&#xff0c;内…
阅读更多...
JVM参数列表

JVM参数列表

-client :设置JVM使用client模式,特点启动较快(神机不明显(I5/8G/SSD)) -server :设置JVM使用server模式。64位JDK默认启动该模式 -agentlib:libname[options] :用于加载本地的lib -agentlib:hprof :用于获取JVM的运行情况 -agentpath:pathnamep[options] :加载制定路径的本…
阅读更多...
共享内存详解

共享内存详解

共享内存是操作系统在内存中开辟一块空间&#xff0c;通过页表与共享区建立映射关系&#xff0c;使两个进程看到同一份资源&#xff0c;实现进程间通信。 1、创建共享内存 参数&#xff1a;第一个参数为key&#xff0c;一般使用ftok()函数生成&#xff0c;key值不能冲突&#…
阅读更多...
副业天花板流量卡推广，小白也可轻松操作

副业天花板流量卡推广，小白也可轻松操作

在如今的互联网时代&#xff0c;手机已经不仅仅是一款工具&#xff0c;更像是我们生活中的一部分&#xff0c;那么手机卡也是必需品&#xff0c;但存在的问题就是:很多手机卡的月租很贵&#xff0c;流量也不够用。所以大家都在寻找一个月租低&#xff0c;流量多的卡&#xff0c…
阅读更多...
Java-Doc

Java-Doc

Java-Doc javdoc命令是用来生成自己的API文档的 参数信息&#xff1a;author作者名version版本号since知名需要最早使用的jdk版本param参数名return返回值情况throws异常抛出情况 1.参数信息的使用&#xff1a; 未完待续... ...
阅读更多...
【好消息】思维100活动历年真题模拟题700多道上线了，供反复吃透

【好消息】思维100活动历年真题模拟题700多道上线了，供反复吃透

今天是星期五&#xff0c;距离4月20日举办的上海小学生 2024年春季思维100活动线上比赛还有8天的时间&#xff0c;明天、后天的周末是可以用来备考的大块时间&#xff0c;报名了的同学要充分利用了。 为了帮助各位小朋友了解思维100活动的历年考试真题、官方发布的参考样题&…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023