如前《STM32学习和实践笔记(4): 分析和理解GPIO_InitTypeDef GPIO_InitStructure (b)(含memory mapping图)-CSDN博客
》中所写,
STM32一共有4GB的地址,对所有的寄存器、存储器、外设等进行统一编址。
每一个地址对应一个字节,每一个字节含有8位。
而STM的寄存器,都是32位的,所以一个寄存器就要占用4个地址,因为4个地址,每一个8位,才能凑够32位啊。
比如下面这个寄存器:
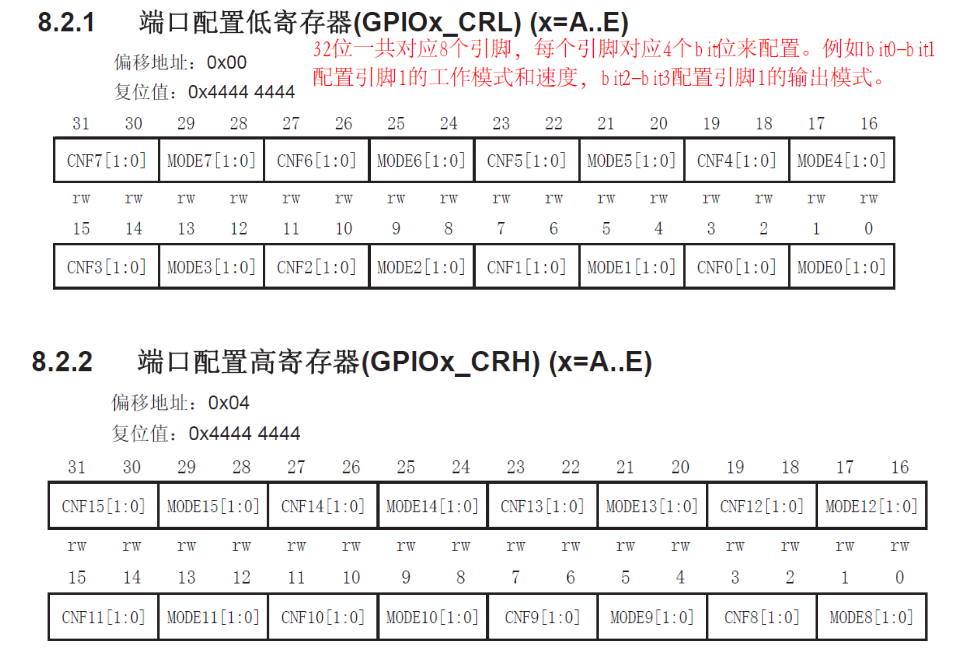

控制PortC上的那些引脚的寄存器,他们的址址是从0x4001 1000一路排到0x4001 13FF,一共有1024个地址(也就是1K),其中,最开始的4个地址,就分配给了![]()
在上面的那些32位的寄存器里,假定我操作时,我只想操作其中的1位,而不想操作其余位时,应该怎么办?
当然也可以在软件上做一系列的操作来实现。
但是STM32在硬件上做了一个处理,就是将那些位带区里的每一个bit,都扩展成32位,而放到位带别名区。
它位分别位于:

其位与地址检测位的规则是:

举例来说明:
假定位带区(bit band region)的第一个地址,也就是基地址0x40000000保存的这个byte的8个bit,因为其每一个bit都要膨胀成32位,这样,它在位带别名区,就需要4个地址来保存,这四个地址的起始地址,根据上面这个公式来计算如下:
第0个bit位在位带别名区(bit band Alias)的起始地址是:
AliasAddr = 0x42000000+ (A-0x40000000)*8*4 +n*4
=0x42000000+ (0x40000000-0x40000000)*8*4 +0*4
=0x42000000
第1个bit位在位带别名区(bit band Alias)的起始地址是:
AliasAddr = 0x42000000+ (A-0x40000000)*8*4 +n*4
=0x42000000+ (0x40000000-0x40000000)*8*4 +1*4
=0x42000000+1*4
=0x42000004
依此类推,第7个bit位在位带别名区(bit band Alias)的起始地址是:
AliasAddr = 0x42000000+ (A-0x40000000)*8*4 +n*4
=0x42000000+ (0x40000000-0x40000000)*8*4 +7*4
=0x42000000+7*4(28用16进制是0x1C)
=0x4200001C
(注意这里计算是32位的起始地址,所以实际上第7个bit位占了从0x4200001C到0x42000020的4个地址)
所以,位带区的基地址0x40000000保存的这个byte的8个bit,在位带别名区,用了位带别名区的从
0x42000000到0x42000020的32个地址。
类似地,假定位带区(bit band region)的地址是0x40000001,那么同样根据上述公式,也能得到正确的地址,计算的结果,就是在基地址基础上增加了32位的偏移而已。这很简单。
简言之,就是用位带别名区的32位来表示位带区的一位。
一位只有0和1两种情况。那么对应的这32位数据,也可以只用0来表示0,用1来表示1。
这样,当我在位带区里的某一个地址的里的byte里的一位操作时,我就根据某个32位的起始地址,来对这32位进行操作。这很简单。
硬件做了这样的设计,就很方便地能对位带区的那些32位寄存器的某一位操作,而不会影响其余位了。
位带操作的优点
(1)控制GPIO口输入输出非常简单。
(2)操作串行接口芯片非常方便(DS1302、74HC595等)。
(3)代码简洁,阅读方便。
这就是要搞这个位带区和位带别名区的意义所在!
------------------------------------------------------------
可以把上面的两个公式合并成下面这一个公式:

当调用这个合并公式时,传进来的是这两个参数:A和n
A:位带区的地址(无论是从0x40000000开始的外设位带区,还是众0x200000000开始的SRAM的位带区),以及n:该地址里的byte里的第n个bit位.
很明显,假定A为0x40000001,经过((A & 0xF0000000)+0x02000000这样运算,得到的就是0x42000000
而如果A为0x20000001,经过((A & 0xF0000000)+0x02000000这样运算,得到的就是0x22000000,
所以这部分实现了与前面的那个没合并公式时同样的效果。
而((A &0x000FFFFF),实现的效果,与(A-0x40000000)实际的效果完全相同,就是算出与基地址的差值。
左移5位相当于*32,左移2位相于*4。
所以,合并公式完全实现了前面两个公式的结果。
通过写出上面这个笔记博文,我算是完全理解了~非常清楚~真好~