NO.116 填充每个节点的下一个右侧节点指针
给定一个 完美二叉树 ,其所有叶子节点都在同一层,每个父节点都有两个子节点。二叉树定义如下:
struct Node {
int val;
Node *left;
Node *right;
Node *next;
}
填充它的每个 next 指针,让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点,则将 next 指针设置为 NULL。
初始状态下,所有 next 指针都被设置为 NULL。
示例 1:

输入:root = [1,2,3,4,5,6,7] 输出:[1,#,2,3,#,4,5,6,7,#] 解释:给定二叉树如图 A 所示,你的函数应该填充它的每个 next 指针,以指向其下一个右侧节点,如图 B 所示。序列化的输出按层序遍历排列,同一层节点由 next 指针连接,'#' 标志着每一层的结束。
示例 2:
输入:root = [] 输出:[]
本题难点在于如何填充每个节点的next 指针,让这个指针指向其下一个右侧节点。如何获取队列中下一个节点,我们还没有遍历到下一个节点,怎么能获取下一个节点的指针呢?
这里的思路是保存上一个遍历节点的指针,让它的next指针指向当前节点。是不是很巧妙,和我们自然的思路不太一样。
因为我们用到了前节点的变量,而头节点并没有前节点,所以需要单独考虑情况。
完整代码如下
class Solution {
public:
Node* connect(Node* root) {
queue<Node*> que;
if(root != NULL){
que.push(root);
}
while(!que.empty()){
// 如何判断每一层的个数
//记录队列的大小
int size = que.size();
//建立当前节点
Node* node;
Node* prenode;
// 遍历队列,放入数组
for(int i = 0; i < size; i++ ){
//如果遍历到这一层的头节点
if(i == 0){
node = que.front();
prenode = node;
}
else{
//出队列第一个元素放入数组
node = que.front();
//上一个节点的next指针指向当前节点
prenode->next = node;
//将前节点更新为当前节点
prenode = node;
}
//将左右节点入队列
if(node->left) que.push(node->left);
if(node->right) que.push(node->right);
//将当前节点弹出
que.pop();
}
//这一层遍历完,将最后一个元素的next设置为null
node->next = NULL;
}
return root;
}
};总结与反思
层序遍历最关键的是深刻理解整个for循环是每一层遍历的核心,这样添加代码就会更加自如,知道是在层前还是层中还是层后。
写完代码,可以验证一遍测试用例,发现bug,避免显而易见的错误。
NO.117 填充每个节点的下一个右侧节点指针II
给定一个二叉树:
struct Node {
int val;
Node *left;
Node *right;
Node *next;
}
填充它的每个 next 指针,让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点,则将 next 指针设置为 NULL 。
初始状态下,所有 next 指针都被设置为 NULL 。
示例 1:
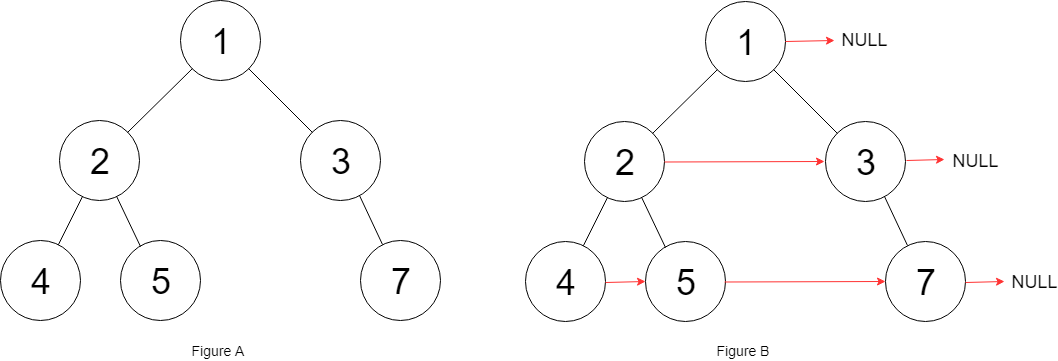
输入:root = [1,2,3,4,5,null,7] 输出:[1,#,2,3,#,4,5,7,#] 解释:给定二叉树如图 A 所示,你的函数应该填充它的每个 next 指针,以指向其下一个右侧节点,如图 B 所示。序列化输出按层序遍历顺序(由 next 指针连接),'#' 表示每层的末尾。
示例 2:
输入:root = [] 输出:[]
这道题目说是二叉树,但116题目说是完整二叉树,其实没有任何差别,一样的代码一样的逻辑一样的味道
完整代码如下
class Solution {
public:
Node* connect(Node* root) {
queue<Node*> que;
if(root != NULL){
que.push(root);
}
while(!que.empty()){
// 如何判断每一层的个数
//记录队列的大小
int size = que.size();
//建立当前节点
Node* node;
Node* prenode;
// 遍历队列,放入数组
for(int i = 0; i < size; i++ ){
//如果遍历到这一层的头节点
if(i == 0){
node = que.front();
prenode = node;
}
else{
//出队列第一个元素放入数组
node = que.front();
//上一个节点的next指针指向当前节点
prenode->next = node;
//将前节点更新为当前节点
prenode = node;
}
//将左右节点入队列
if(node->left) que.push(node->left);
if(node->right) que.push(node->right);
//将当前节点弹出
que.pop();
}
//这一层遍历完,将最后一个元素的next设置为null
node->next = NULL;
}
return root;
}
};NO.104 二叉树的最大深度
给定一个二叉树 root ,返回其最大深度。
二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。
示例 1:
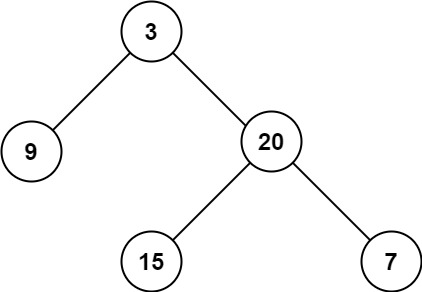
输入:root = [3,9,20,null,null,15,7] 输出:3
示例 2:
输入:root = [1,null,2] 输出:2
完整代码如下
class Solution {
public:
int maxDepth(TreeNode* root) {
queue<TreeNode*> que;
//记录最大深度
int depth = 0;
if(root != NULL){
que.push(root);
}
while(!que.empty()){
// 如何判断每一层的个数
//记录队列的大小
int size = que.size();
// 遍历队列,放入数组
for(int i = 0; i < size; i++ ){
TreeNode* node = que.front();
//将左右节点入队列
if(node->left) que.push(node->left);
if(node->right) que.push(node->right);
//将当前节点弹出
que.pop();
}
depth++;
}
//循环结束说明遍历完最后一层,返回深度
return depth;
}
};NO.111 二叉树的最小深度
给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明:叶子节点是指没有子节点的节点。
示例 1:
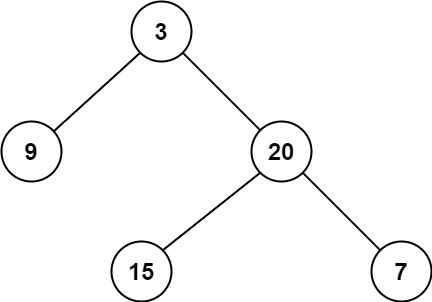
输入:root = [3,9,20,null,null,15,7] 输出:2
示例 2:
输入:root = [2,null,3,null,4,null,5,null,6] 输出:5
完整代码如下
class Solution {
public:
int minDepth(TreeNode* root) {
queue<TreeNode*> que;
//记录深度
int depth = 0;
if(root != NULL){
que.push(root);
}
while(!que.empty()){
// 如何判断每一层的个数
//记录队列的大小
int size = que.size();
// 遍历队列,放入数组
depth++;
for(int i = 0; i < size; i++ ){
TreeNode* node = que.front();
//一旦找到叶子节点就返回深度
if(node->left == NULL && node->right == NULL)
return depth;
//将左右节点入队列
if(node->left) que.push(node->left);
if(node->right) que.push(node->right);
//将当前节点弹出
que.pop();
}
}
return 0;
}
};