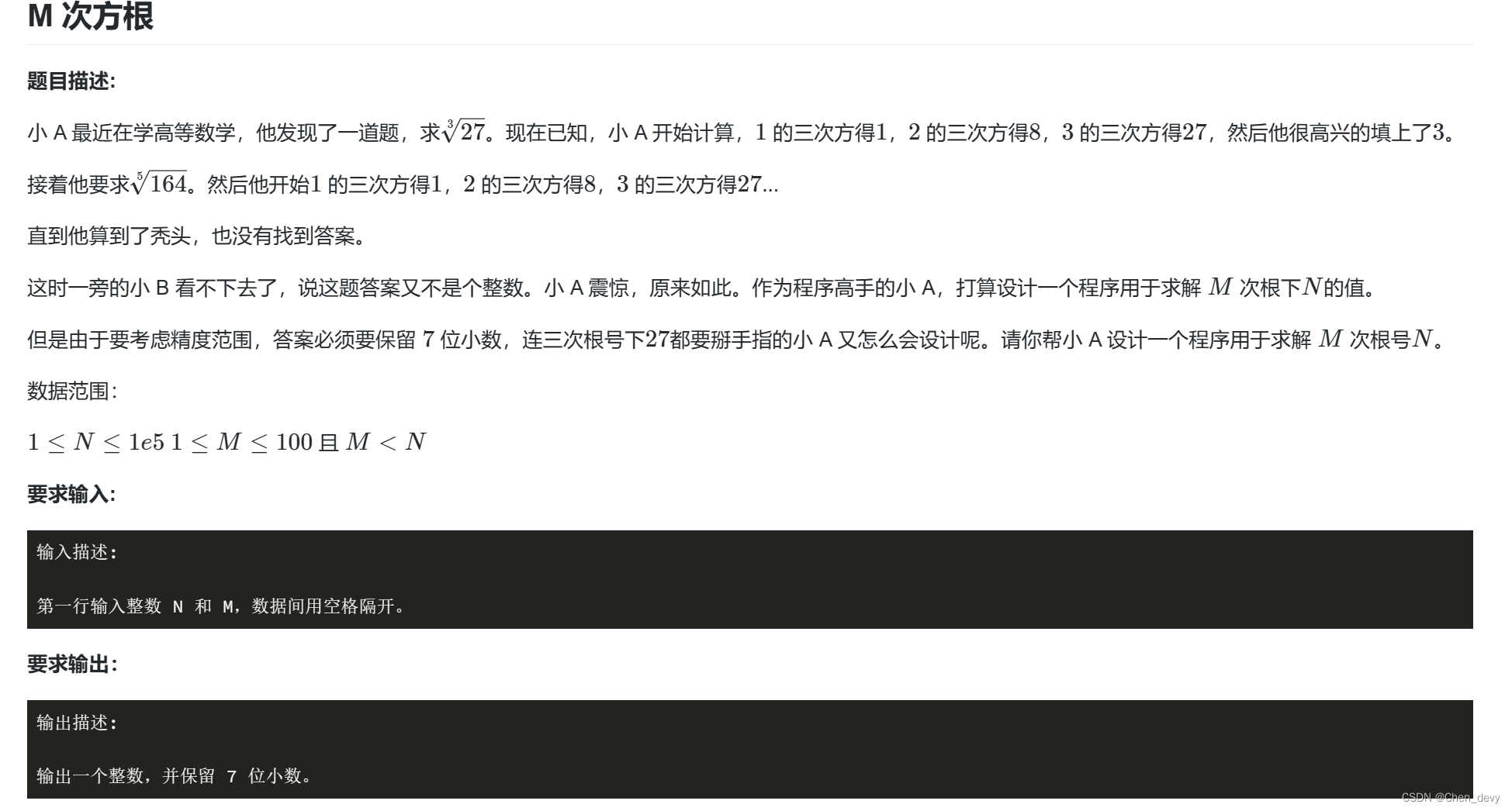
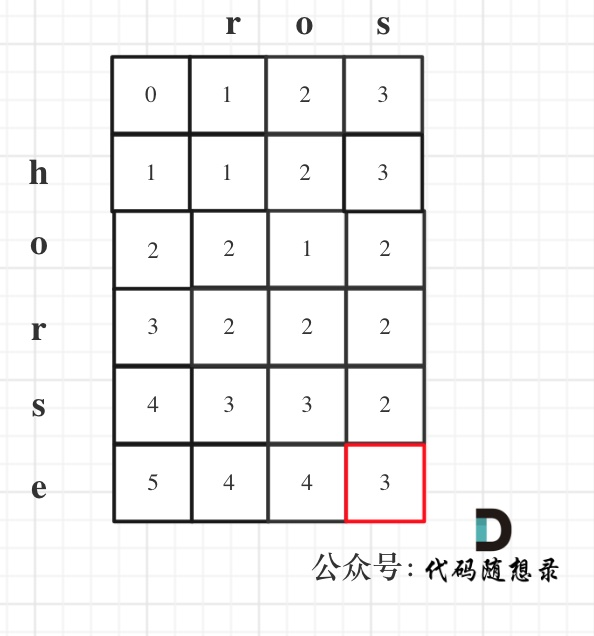
总结一下这类题型的思路:
每一步所求的最优解 = 上一步的最优解 + 这一步的情况
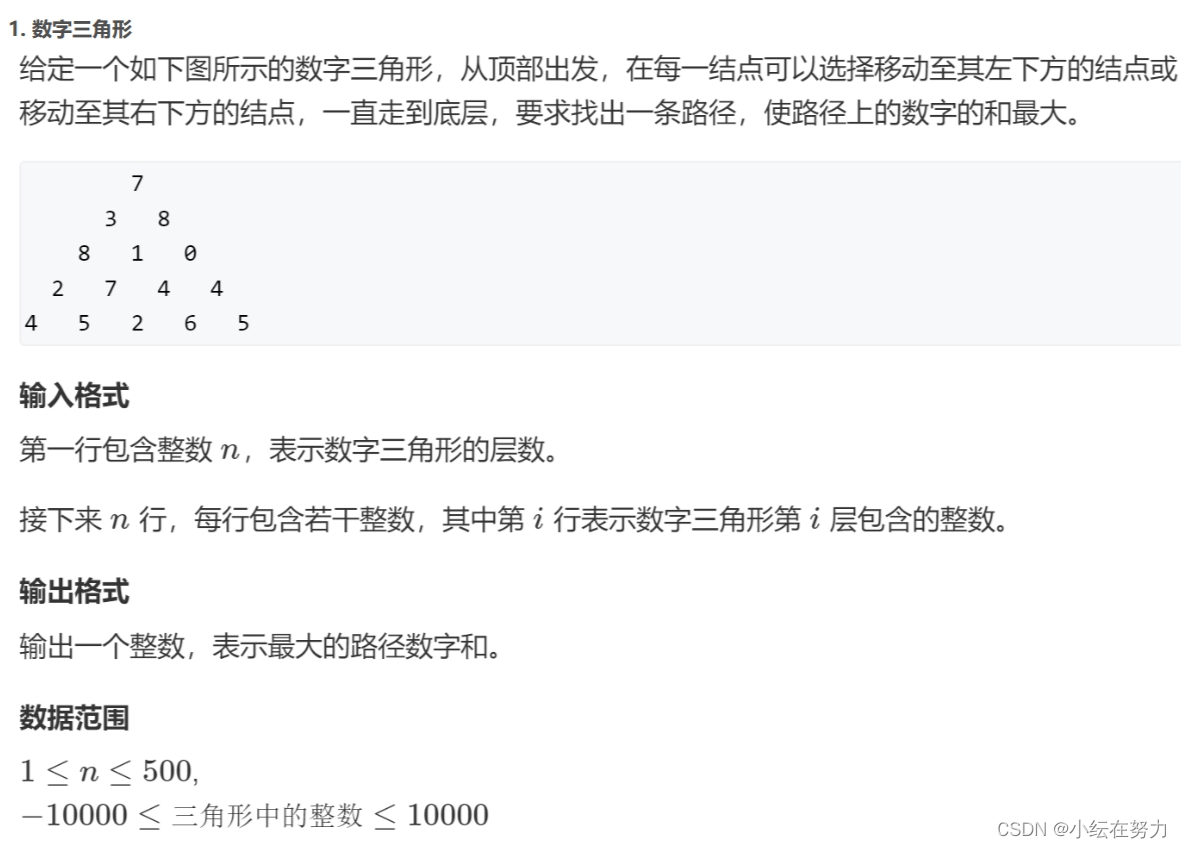
1.数字三角形
主要思路:
1.到达每一个位置的最大和等于前一步最大和加上这一位置的值,而前一步要么是从左上下来,要么是从右上下来,这样就将原问题分解了
2.记得初始化dp数组,不然里面元素初值是不确定的
//数字三角形
//给定一个三角形,每一个结点选择移动至左下或者右下,
//找出一条路径使路径上数字和最大
#include<stdio.h>
int max(int a, int b){
if(a>b){
return a;
}
else
return b;
}
int main(){
int n;
scanf("%d",&n);//输入三角形行数
int a[n+1][n+1],i,j;
int dp[n+1][n+1];//记录动态变化
for(i=0;i<=n;i++){
for(j=0;j<=n;j++){
dp[i][j]=-1;
}
}
for(i=1;i<=n;i++){
for(j=1;j<=i;j++){
scanf("%d",&a[i][j]);
}
}
dp[1][1]=a[1][1];
for(i=2;i<=n;i++){
for(j=1;j<=i;j++){
dp[i][j]=max(dp[i-1][j-1],dp[i-1][j])+a[i][j];
}
}
int the_max=0;
for(j=1;j<=n;j++){
if(dp[n][j]>the_max){
the_max=dp[n][j];
}
}
printf("%d",the_max);
return 0;
}2.最低通行费


//最低通行费
//N*N矩阵,左上角进,右下角出,不能斜对角通过,求最小和
#include<stdio.h>
int min(int a, int b){
if(a>b)
return b;
else
return a;
}
int main(){
int N;//矩阵宽度
scanf("%d",&N);
int a[N+1][N+1];
int i,j;
for(i=1;i<=N;i++){
for(j=1;j<=N;j++){
scanf("%d",&a[i][j]);
}
}
int dp[N+1][N+1];//动态数组
//初始化 ,求最小值,所以初始化尽可能大
for(i=0;i<=N;i++){
for(j=0;j<=N;j++){
dp[i][j]=10000000;
}
}
//完善初始化(很重要的一步)
//左上角元素
dp[1][1]=a[1][1];
//第一行只能从左边来
for(j=2;j<=N;j++){
dp[1][j]=dp[1][j-1]+a[1][j];
}
//第一列只能从上面来
for(i=2;i<=N;i++){
dp[i][1]=dp[i-1][1]+a[i][1];
}
//必须在2N-1个时间过去,所以只能从左边或者上边过来
for(i=2;i<=N;i++){
for(j=2;j<=N;j++){
dp[i][j]=min(dp[i][j-1],dp[i-1][j])+a[i][j];
}
}
printf("%d",dp[N][N]);
return 0;
}3.方格取数

主要思路:
1.两条路线一起走,每次记录到达两个点位置可取最大值,本来是用一个四维数组dp[i1][j1][i2][j2],但是我们发现每次只能往左或者往下走一步,说明每一步横纵坐标的和是相同的,就可以设一个k表示横纵坐标和,且i1+j1=k,i2+j2=k,用一个三维数组dp[k][i1][i2]替代四维,而可以降低时间复杂度(重要思维)
2.每一个坐标处的最大值,都等于上一步的最大值加上这一步可以获得的值,而上一步k-1有四种可能,依次比较即可
注意点:
1.给dp定义和初始化时要注意,从0,0开始赋初值(不然会访问到无值的地址),并且第三维度的大小是N*2+1
2.三重循环里的判断语句防止下标越界
3.不用根据题目意思将遍历过的地方设置为0,因为不是一次性的过程,这里一步一步只能往右边或者下面走是不会出现重复的
4.要注意,当两条路线的两个点不是同一个点时才能相加,否则会重复相加
//方格取数
//某些放入数据,其他为0,两条路径,和最大,向下或向右走
/*输入
8
2 3 13
2 6 6
3 5 7
4 4 14
5 2 21
5 6 4
6 3 15
7 2 14
0 0 0
*/
//输出:67
#include<stdio.h>
int max(int a, int b){
return a > b ? a : b ;
}
int main(){
int N;//方格N*N
scanf("%d",&N);
int np[N+1][N+1];
//初始化
int i,j,k;
for(i=1;i<=N;i++){
for(j=1;j<=N;j++){
np[i][j]=0;
}
}
//放入数据
int a,b,c;
scanf("%d %d %d",&a,&b,&c);
while(a!=0 || b!=0 || c!=0){
np[a][b]=c;
scanf("%d %d %d",&a,&b,&c);
}
//dp[k][i1][j1]
//i1+j1=i2+j2=k
int dp[N*2+1][N+1][N+1];
//初始化dp,注意下标范围
for(i=0;i<=N*2;i++){
for(j=0;j<=N;j++){
for(k=0;k<=N;k++){
dp[i][j][k]=0;
}
}
}
dp[2][1][1]=np[1][1];//左上角
int i1,i2;
for(k=2;k<=N*2;k++){
for(i1=1;i1<=N;i1++){
for(i2=1;i2<=N;i2++){
int j1=k-i1;
int j2=k-i2;
//防止下标越界
if(j1>=1 && j1<=N && j2>=1 && j2<=N){
int t=np[i1][j1];
if(i2!=i1) t+=np[i2][j2];//防止重复累加,一个地方只能过一次
//np[i1][j1]=np[i2][j2]=0;
//不能设为0,因为本来就是不会重复走的,如果设为0会影响其他位置的计算,导致所求值偏小
dp[k][i1][i2]=max(dp[k][i1][i2],dp[k-1][i1-1][i2-1]+t);
dp[k][i1][i2]=max(dp[k][i1][i2],dp[k-1][i1][i2-1]+t);
dp[k][i1][i2]=max(dp[k][i1][i2],dp[k-1][i1-1][i2]+t);
dp[k][i1][i2]=max(dp[k][i1][i2],dp[k-1][i1][i2]+t);
}
}
}
}
printf("%d",dp[N*2][N][N]);
return 0;
}