二分查找算法

什么是二分查找算法

• 枚举查找即顺序查找*，实现原理是逐个比较数组 a[0:n-1] 中的元素，直到找到元素 x 或搜索整个数组后确定 x 不在其中。最坏情况下需要比较N次，时间复杂度是 O(n)，属于线性阶算法。*

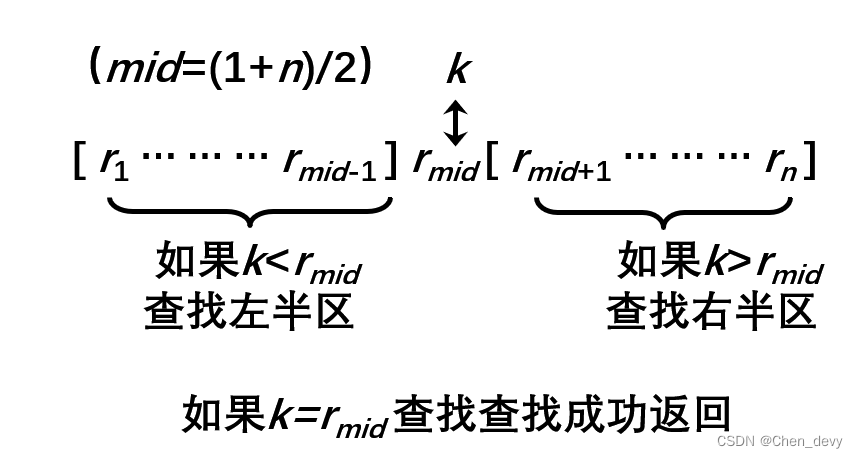
• 二分查找，也称为折半查找，是一种在有序数组或列表中查找特定元素的高效算法。它的基本思想是通过将查找范围逐渐缩小一半的方式来确定目标元素的位置。具体来说，它的步骤如下：

1. 初始化：首先确定整个有序数组或列表作为初始的查找范围。
2. 确定中间位置：计算初始查找范围的中间位置。
3. 比较目标值：将目标值与中间位置的元素进行比较。
4. 调整查找范围：根据比较结果，如果目标值等于中间位置的元素，则找到目标元素，算法结束；如果目标值小于中间位置的元素，则在左半部分继续查找；如果目标值大于中间位置的元素，则在右半部分继续查找。
5. 重复步骤 2 到步骤 4，直到找到目标元素或查找范围为空。

二分查找算法的关键在于每一步将查找范围减半，因此它的时间复杂度为 O(log n)，其中 n 为数组或列表的大小。这使得它在处理大规模数据时具有较高的效率。需要注意的是，二分查找要求数组或列表是有序的，否则无法保证正确性。

二分查找的示意图：

Step 1:

假设存在一个有序数组：
下标[ 0   1   2   3   4   5   6   7   8    9    10   11   12 ]
数据[ 7   14  18  21  23  29  31  35   38   42   46   49  52 ]
      ↑                                                   ↑
    low=0                                              high=12

                            mid=(low+high)/2
                            mid=(0+12)/2
                            mid=6
                            [mid]=31 > 14，所以选择左半部分

操作：
    此时令low不变，high=mid-1=5

Step 2:

下标[ 0   1   2   3   4   5   6   7   8    9    10   11   12 ]
数据[ 7   14  18  21  23  29  31  35   38   42   46   49  52 ]
      ↑                   ↑
   low=0                 high=5

            mid=(low+high)/2
            mid=(0+6)/2
            mid=3
            [mid]=21 > 14，所以选择左半部分

操作：
    此时令low不变，high=mid-1=2

Step 3:

下标[ 0   1   2   3   4   5   6   7   8    9    10   11   12 ]
数据[ 7   14  18  21  23  29  31  35   38   42   46   49  52 ]
      ↑       ↑
   low=0    high=2

            mid=(low+high)/2
            mid=(0+2)/2
            mid=1
            [mid]=14 = 14  找到答案

操作：
    返回下标

整数二分法常用算法模板

// 在单调递增序列a中查找>=x的数中最小的一个（即x或x的后继）
while (low < high)
{
    int mid = (low + high) / 2;
    if (a[mid] >= x)
        high = mid;

    else
        low = mid + 1;
}

// 在单调递增序列a中查找<=x的数中最大的一个（即x或x的前驱）
while (low < high)
{
    int mid = (low + high + 1) / 2;

    if (a[mid] <= x)
        low = mid;

    else
        high = mid - 1;
}

二分查找算法例题

例题一：分巧克力问题

输入示例：

2 10 6 5 5 6

输出示例：

2

解题思路：枚举所有的情况，从小到大排序进行切割，直到找到满足要求的巧克力边长。
求一块长方形$(h\ast w)$最多被分成正方形$(len\ast len)$巧克力个数为：$$num=(h/len)\ast (w/len)$$
为了减少运行时间，避免超时，采用二分查找的方法。
这个题解的解题思路非常清晰，我来为你总结一下：

解题思路

1. 问题描述：
   给定 n 块巧克力和 k 个小孩，每块巧克力的长和宽分别为h[i]和 w[i]。需要确定可以切割成 k 个相同大小的巧克力块的最大边长。

2. 枚举所有情况：

   • 题目要求找到满足要求的巧克力边长，这意味着需要枚举所有可能的边长，从小到大排序进行切割。

3. 计算巧克力个数：

   • 对于给定的长方形巧克力，将其切割成正方形（边长为 len）后，可以得到的正方形巧克力个数为 $num=(h[i]/len)\ast (w[i]/len)$。

4. 二分查找：

   • 为了减少运行时间，避免超时，采用二分查找的方法。首先确定二分查找的上下界，其中下界至少为 1。然后，在二分查找的过程中，不断调整中间值（边长），直到找到满足要求的最大边长。

5. 判断函数：

   • 设计判断函数 pd()，用于确定给定边长是否能够满足条件，即是否可以切割成至少 k 个相同大小的巧克力块。

通过枚举、计算和二分查找的结合，能够高效地解决给定问题。在确保了正确性的同时，通过二分查找的方式，也使得算法的时间复杂度得到了有效地降低，提高了算法的效率。

#include<bits/stdc++.h>

using namespace std;
const int MAXN=100010;
int n,k;//巧克力的个数 小孩儿的个数
int h[MAXN],w[MAXN];

bool pd(int l)
{
    int sum=0;
    for(int i=0; i<n; i++)
    {
        sum+=(h[i]/l)*(w[i]/l);
        if(sum>=k)
        {
            return true;
        }
    }
    return false;
}

int main()
{
    cin>>n>>k;//输入 巧克力 和 小孩儿的个数
    for(int i=0; i<n; i++)
        cin>>h[i]>>w[i];//每块巧克力的长和宽

    //找到二分查找的上界
    int high=0;

    for(int i=0; i<n; i++)
    {
        high=max(high,h[i]);
        high=max(high,w[i]);
    }
    // 二分下届由题意可得至少为1
    int low=1;

    // 由于本题目就是求符合要求的Mid 值所以要将mid定义在二分查找外边
    int mid=0;
    while(low<high)
    {

        mid = (low + high+1) / 2;
        if(pd(mid))
            low=mid;
        else
            high = mid - 1;

//        cout<<low<<" "<<high<<endl;
    }

    //因为low=high所以输出哪一个都一样
    cout<<low;
    return 0;
}

例题二：M次方根

输入样例:

27 3

输出样例：

3.0000000

运行限制：

最大运行时间：1s
最大运行内存: 256M

注意：
1. 请严格按要求输出，不要画蛇添足地打印类似：“请您输入…” 的多余内容。
2. 不要调用依赖于编译环境或操作系统的特殊函数。
3. 所有依赖的函数必须明确地在源文件中。
4. 不能通过工程设置而省略常用头文件。

题型通用模板：

//模版一：实数域二分，设置eps法

//令 eps 为小于题目精度一个数即可。比如题目说保留4位小数，0.0001 这种的。那么 eps 就可以设置为五位小数的任意一个数 0.00001- 0.00009 等等都可以。

//一般为了保证精度我们选取精度/100 的那个小数，即设置 eps= 0.0001/100 =1e-6

while (l + eps < r)
{
    double mid = (l + r) / 2;

    if (pd(mid))
        r = mid;
    else
        l = mid;
}

//模版二：实数域二分，规定循环次数法
//通过循环一定次数达到精度要求，这个一般 log2N < 精度即可。N 为循环次数，在不超过时间复杂度的情况下，可以选择给 N 乘一个系数使得精度更高。

    for (int i = 0; i < 100; i++)
{

    double mid = (l + r) / 2;
    if (pd(mid))
        r = mid;
    else
        l = mid;
}

判定条件pd():

double pd(double a,int m)
{
    double c=1;
    while(m>0)
    {//求a的m次方
        c=c*a;
        m--;
    }
    
    if(c>=n)//如果C大于等于原来的数 n
        return true;
    else
        return false;
}

解题分析：

1. 问题理解：

   • 该程序解决了一个求解数的 M 次方根的问题，其中给定了一个数 n 和一个整数m，需要求出 n 的 m 次方根。

2. 输入与初始化：

   • 程序首先通过输入流 cin 读取了两个变量 n 和 m。
   • 初始化了两个变量 l 和 r，分别表示二分查找的左右边界，初始值分别为0和 n。

3. 二分查找：

   • 采用了实数域二分的方式进行查找，即在区间 [l, r] 上进行二分查找。
   • 在 while 循环中，通过计算中间值 mid，并调用函数 pd(mid, m) 判断 mid 的 m 次方是否大于等于 n，来决定下一步搜索的方向。
   • 不断调整边界 l 和 r，直到满足精度要求（eps）。

4. 判断函数 pd：

   • 函数pd用于判断给定的数a的 m 次方是否大于等于 n。如果是，则返回 true，否则返回 false。

5. 输出结果：

   • 输出结果时，采用了 cout 进行输出，并通过 setprecision(7) 设置了输出的精度为 7 位小数。

算法复杂度分析

• 时间复杂度：由于采用了实数域二分查找，算法的时间复杂度为 O(log n)，其中 n 为目标数。
• 空间复杂度：算法使用了常数级别的额外空间，空间复杂度为 O(1)。

题解代码：

#include <cstdio>
#include <iostream>
#include<iomanip> //用于浮点数输出
using namespace std;

double n,l,r,mid;
double eps=1e-8;

bool pd(double a,int m)
{
    double c=1;
    while(m>0)
    {
        c=c*a;
        m--;
    }
    if(c>=n)
        return true;
    else
        return false;
}

int main()
{
    int m;
    cin>>n>>m;
//设置二分边界
    l=0,r=n;
//实数二分
    while (l + eps < r)
    {
        double mid = (l + r) / 2;
        if (pd(mid,m))
            r = mid;
        else
            l = mid;
    }

    cout<<fixed<<setprecision(7)<<l;
    //一般使用print
    //printf("%x.yf",n)
    //其中X是固定整数长度，小数点前的整数位数不够，会在前面补0
    //y是保留小数位数，不够补零
    //printf("%.7f",l);
    return 0;
}

感谢阅读！！！
【数据结构与算法】系列文章链接: 【数据结构与算法】递推法和递归法解题（递归递推算法典型例题）
【数据结构与算法】系列文章链接: 【数据结构与算法】C++的STL模板（迭代器iterator、容器vector、队列queue、集合set、映射map）以及算法例题
【数据结构与算法】系列文章链接: 【数据结构与算法】搜索算法（深度优先搜索 DFS和广度优先搜索 BFS）以及典型算法例题