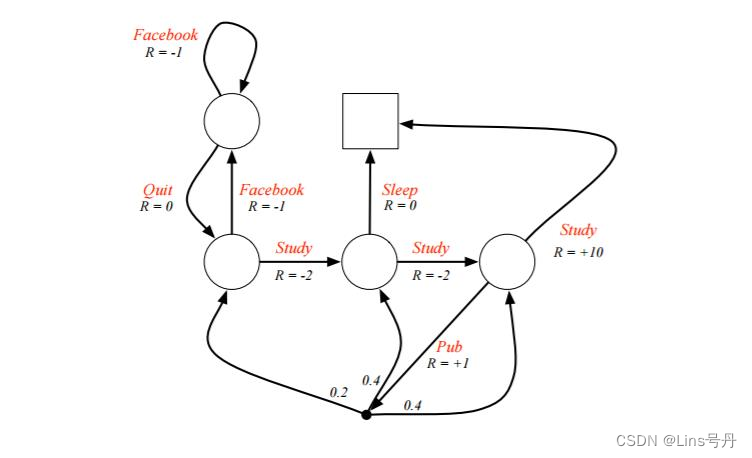
总结,建议看EXCEL的《算法》页签,不然感觉有点乱
| 备注 | 原理/步骤 | 时间复杂度 | 空间复杂度 | |||||||||||||||||||||||
| 串的应用 | 模式匹配 | 简单/暴力 | O(mn) | |||||||||||||||||||||||
| KMP | O(m+n) | |||||||||||||||||||||||||
| 树的应用 | 树 | 哈夫曼树 1、带权路径长度WPL 2、外部排序-最佳归并树 | 1、哈夫曼树的度,只有0和m(m叉树)(王道P176) 2、哈夫曼编码,是从根结点到叶子结点的路径上的01组合(王道P180.T4) 3、同一组编码/权值,构造出来的哈夫曼树可以不同【自己举个例子就知道了】(王道P180.T6A) 4、路径长度指:Σ(叶子结点的值 x 到根的长度数),之和【领悟:哈夫曼树的构造,除了第一次用m个数据(如0、2、3),其他每次只用m-1个数据(因为有1个数据是来自下一层的和)】 王道.P359.T07 | |||||||||||||||||||||||
| 并查集 1、Kruskal,克鲁斯卡尔(王道.P182.T10) 2、无向图的连通性判断 | ||||||||||||||||||||||||||
| 图的存储 | 邻接矩阵 | O( |V|2 ) | ||||||||||||||||||||||||
| 邻接表 | 删除,某个顶点相关的所有边 有向图:O( |V| + |E| ) | 无向图:O( |V| + 2|E| ) 有向图:O( |V| + |E| ) | ||||||||||||||||||||||||
| 十字链表(有向图) | 顶点表:[data,edge1,edge2] 边表:[弧尾点,弧头点,弧头指针,弧尾指针,info] | O( |V| + |E| ) | ||||||||||||||||||||||||
| 邻接多重表(无向图) | 顶点表:[data,edge] 边表:[点1,点2,指针1,指针2,info] | O( |V| + |E| ) | ||||||||||||||||||||||||
| 图的遍历 | BFS,广度优先 | 1、队列 2、相当于树的层次遍历 | 像波纹一样推开遍历 | 邻接矩阵:O( |V|2 ) 邻接表:O( |V| + |E| ) | O( |V| ) | |||||||||||||||||||||
| DFS,深度优先 | 1、栈 2、相当于树的先序遍历 3、可用于判断有向图是否有回路 4、逆拓扑排序(王道P210.T11) | 1、一条路走到黑 2、再退一步,再走到黑 | ||||||||||||||||||||||||
| 图的应用 | I 最小生成树 1、权值的和为最小 2、没有权值相同的边,生成树的树形才唯一 3、最小生成树的代价一定是唯一的(王道P228.T18) | Prim,普利姆 只与点有关 贪心算法 | 1、n个结点,时间复杂度,与边无关(因为是选n-1边,没选到的边,再多也无用),适合稠密图 2、n个结点,1个最小的,其余n-1个相等的值,从不同的顶点开始Prim算法,则会得到n-1种不同的最小生成树(王道.P228.T18.III) | 1、一个顶点选连接的最小的边(最小边:将已经连接的点,作为整体,看与未连接的边的权重/值,最小的一个),选完:若构成环,则去掉刚选的边,退到上一个顶点 2、结束:所有顶点都连接时 | O( |V|2 ) | |||||||||||||||||||||
| 普克(扑克) | Kruskal,克鲁斯卡尔 只与边有关 贪心算法 | 适合边稀疏 | 1、所有边从小到大排序,依次选择:若构成环,去掉继续选下一个 2、结束:所有顶点都连接时 | O( nlog2n ),n是边 | ||||||||||||||||||||||
| II 最短路径 简单路径 | BFS,广度优先 | 1、无权单源(点到点) 2、只能无向图(权值为1或相同) | / | 邻接矩阵:O( |V|2 ) 邻接表:O( |V| + |E| ) | ||||||||||||||||||||||
| 广迪弗(甘道夫) | Dijkstra,迪杰斯特拉 贪心算法 | 1、带权单源(点到点) 2、负权值、负回路不适用 | 1、主要3个元素:标记、距离、前驱 2、选一个点先初始化 3、①选中距离最小且未标记的点,标记置为True;②更新由点到其他未标记的距离、前驱 4、结束:所有结点标记都为True | O( |V|2 ) | ||||||||||||||||||||||
| Floyd,弗洛伊德 | 1、带权所有顶点 2、负回路不适用 | 1、A[i][j] > A[i][*] + A[*][j],选择一个"点*"作为转中点,到其他点的距离更新 2、每次选择都需要更新邻接矩阵 | O( |V|3 ) | O( |V|2 ) | ||||||||||||||||||||||
| III 有向无环图描述表达式 DAG,Directed Acyclic Graph | 最底层的元素都只有一个 | 1、先按顺序写出所有的字母,作为最底层的元素 2、依次往上连接符号,表示一个小的运算 | ||||||||||||||||||||||||
| IV 拓扑排序 AOV,Activity On Vertex Network | 1、有拓扑序列就不存在回路 ∵要选入度为0,回路是环,不存在入度为0的结点 2、每个顶点出现仅有一次 3、可能排序不唯一 4、A排在B前面,则不存在 B —>A 的路径 | 依次选择入度为0的点 | ||||||||||||||||||||||||
| 逆拓扑排序· | DFS,深度优先,出栈时读出 | DFS,可得逆拓扑顶点有序序列 | 依次选择出度为0的点 | |||||||||||||||||||||||
| V 关键路径 AOE,Activity On Edge Network | 1、缩短所有关键路径上共有的任意一个关键活动的时间,才可以缩短关键路径长度 2、 e(i):事件最早发生时间 l(i):事件最迟发生时间 ae(i):活动最早发生时间 al(i):活动最迟发生时间 d=ae(i)-al(i),为0就是关键活动 | 从起点到结束点,长度最大的路径 | 平均查找长度 ASL 类似EX数学期望 | |||||||||||||||||||||||
| 查找 | 线性结构 | 顺序查找 | 1、数组、链表均可 2、每个元素查找成功的比较次数只与位置有关,与是否有序无关,王道.P253.T2 | O(n) | 一般:ASL成功 = ΣPi(n-i+1) 等概率: ASL成功 = (n+1)/2 ASL不成功 = n+1 王道.P250推导 | |||||||||||||||||||||
| 折半查找 二分查找 | 1、必须有序,且只能用顺序存储(数组) 2、平衡二叉树 3、(low+high)/2 结果:向上取整或向下取整,但一棵树只能二选一,王道.P254.T12/T21 | 查找:O(log2n) 插入删除:O(n) | 等概率:ASL成功 ≈log2(n+1)-1 王道P252例子 P254T13/T18 | |||||||||||||||||||||||
| 分块查找 | 1、块内随意,块间有序;折半查找索引表,顺序查找块内表 2、索引表:一个块的最大的关键字,和第一个元素的位置 3、最理想的块长:√n,且平均查找长度为 (√n) +1 | 1、先查索引表(顺序查找/(数组时)二分查找) 2、块内顺序查找 | (b+1)/2 + (s+1)/2 分为 b 块,每块有 s 个记录,王道.P254.T16 | |||||||||||||||||||||||
| 树形结构 | 二叉排序树BST - 二叉查找树 - 左 < 根 < 右 | 0、空树也是二叉排序树 1、可以形成单支树,查找长度为 n,时间复杂度是O(nlogn) 2、中序遍历,会得到一个递增的序列 3、 叶结点,删除后插入,与原树一定相同 非叶结点,删除后插入,与原树一定不同 (王道.P276.T21) | 左子树结点的值 < 根结点的值 < 右子树结点的值 | 查找:O(log2n)/O(n) 插入删除:O(log2n) | ||||||||||||||||||||||
| 平衡二叉树AVL - 发明者G. M. Adelson-Velsky和E. M. Landis - 是特殊的二叉排序树 | 0、 - 空树也是平衡二叉树 - 平衡因子:左子树高度-右子树高度 - LL、RR、LR、RL 4种破坏平衡的方式 1、左右子树高度差不超过1 2、不一定是完全二叉树 3、 n0=0,n1=1,n2=2 nh = nh-1 + nh-2 +1 构造最大高度 h 的平衡二叉树,所需的最少的结点数nh(王道.P275.T10/T11),此时非叶结点的平衡因子为1(王道.P276.T20) 4、平衡二叉树,叶结点/非叶子结点,删除后插入,与原树可能相同也可能不同(王道.P276.T25) | O(log2n) | O(log2n) | |||||||||||||||||||||||
| B树,多路平衡查找树 |
| 1、每个结点: [(m/2)向上取整]-1 ≤ 关键字 ≤ m-1(王道.P290.T01) 2、平衡因子=0,绝对平衡,所有叶子结点都在同一层 3、高度 h ,m 阶B树:(王道.P291.T06) ①结点数最少:2h - 1(满二叉树) ②结点数最多:mh - 1(满m叉树) 4、外部结点不算层数 5、m阶,n个点,最大高度、最小高度 P287(王道.P291.T08/T09) | ||||||||||||||||||||||||
| B+树 | 1、用于各种索引:文件索引、数据库索引 | |||||||||||||||||||||||||
| 散列表(哈希表) 散列函数(哈希函数) 1、适合关键字集合与地址集合之间存在对应关系 2、平均查找长度ALS - 与表长、元素都无关 - 与散列函数、处理冲突的方法、装填因子有关 3、装填因子α = 已有记录数/表长度 α越大 - 表示哈希表的装满的程度 - 越容易发生冲突(王道.P302.T06) ∴想要提高查找效率,需要减小装填因子 4、探测:插入前检测次数(王道.P302.T07) | 处理冲突的方法1 开放地址法 Hi = [ H(key) + di ] % m 删除时只能是假删除,否则影响查找 | I 线性探测法 | 1、映射后,一直探测到下一个可以存放的地址 2、会出现元素堆积/聚集(同义词与非同义词发生冲突都可以造成堆积),大大降低查询效率 3、细节:空的也会消耗1次对比的机会(王道.P303.T17/T18) | di = 0 1 2 3 … m-1 | 理想情况:O(1) | |||||||||||||||||||||
| II 平方探测法 | 1、m 是一个 4k+3 的质数 2、有效避免堆积 | di = 02 12 -12 22 -22 … k2 -k2 | ||||||||||||||||||||||||
| III 伪随机序列法 | di = 一个随机数列,可以自己定义 | |||||||||||||||||||||||||
| IV 双散列法,再散列法,再哈希法 | k=Hash1(key) d=Hash2(key) 探测顺序:(k+d)%n、(k+2d)%n、(k+3d)%n… | |||||||||||||||||||||||||
| 处理冲突的方法2 拉链法 | 链接法,链接地址法 | 1、不会发生堆积 | 数组下标作为指针的起始,用链表存数据 | 稳定性 | ||||||||||||||||||||||
| 排序 | 插入排序 | 直接插入 | 1、不考虑哨兵的比较 - 最坏的情况需要 n(n-1)/2 次比较 - 最好的情况只要 n-1 次比较,有序,第一个元素视为已经排好序的,后面每个元素都只要比较1次,所以只要n-1次比较 | 1、第1个元素视为有序,无序消耗比较次数 2、第i个元素前面都是有序的 3、从后往前,找插入位置,然后进行插入 | 最好,初始化序列原本有序:O(n) 平均:O(n2/4),所以是O(n2),和最坏一样 最坏,初始化序列刚好逆序:O(n2) | O(1),每次只要常数个辅助单元 | Y,先比较,再移动 | |||||||||||||||||||
|
| 折半插入 二分插入 | 数组 | 因为是在有序表中查找插入位置,所以查找可以先采用二分查找,再移动元素 | O(n2) | O(1) | Y | ||||||||||||||||||||
| 希尔排序 缩小增量排序 | 数组,不适用于链表 | 1、%d 的为一组(d=间隔+1,王道.P316.T08),然后使用直接插入排序同组元素 2、d减小,再进行排序 | 最好/平均:O(n1.3) 最坏:O(n2) | O(1) | N,相同元素在不同组时,可能发生位置变化 | |||||||||||||||||||||
| 交换排序 两两比较,次序相反的就交换,直到所有数据没有反序为止 | 冒泡排序 起泡排序 | - 最坏的情况,刚好逆序,比较和交换次数相同,都需要 n(n-1)/2 次 - 适用于:数组、链表 - 在一趟排序过程中,没有发生交换,则算法可以提前结束 | 1、每次都是从头到尾,两两比较,满足条件的两两交换 2、细节:每次冒泡就确定了本趟“最后元素”的位置,剩余趟数就不用消耗比较次数 王道.P323.T08 | 最好,有序:O(n) 最坏/平均,逆序:O(n2) | O(1) | Y | ||||||||||||||||||||
| 快速排序 递归排序 | 1、待排序列最适合采用:顺序存储(40811T10) 2、"有序快排最慢"原则,有序每次划分是 0 和 n-1 个元素 每次将表分为长度相近的两个子表时最快(王道.P323.T9) 3、递归次数/趟数: - 对尚未确定最终位置的所有元素进行一遍处理。如:第二趟需要都处理左右两个子块才算一趟(王道.P324.T17) - 与初始数据的排列次序有关("有序最慢"原则) - 与划分后的分区处理前后顺序无关(408.10T10) 4、每一趟排序后,基准值元素,会放在最终的位置 | 选一个基准值,用两个前后两个指针 i、j: 1、比基准值大,将元素放在j,然后j=j-1 2、比基准值小,将元素放在i,然后i=i+1 3、与基准值相等,不处理 i==j时,左右继续重复上述操作,递归 | 最好/平均:O(nlog2n),最平衡的划分,每次划分,左右元素个数差不多都是n/2 最坏:O(n2),有序元素 | 递归工作栈,需要空间 最小:O(log2n) 最大:O(n) | N,同右侧的相同元素,都小于基准值,都要移去左边,那么这2个相同的元素相对位置会改变 | |||||||||||||||||||||
| 选择排序 在所有记录中,每次选择最小的,放在最后/前面 | 选择排序 | 1、数组、链表均可 2、比较次数与初始状态无关,n个元素都需要 n-1 趟 | 1、每次都要遍历排好序之后的待排序列 2、选择最小的数,与无序的第一个数交换 | 比较次数:O(n2),2层for循环 移动次数:O(n) | O(1) |
| ||||||||||||||||||||
| 堆排序 | 1、在1亿个数里面找出100个最小值,用大根堆(根 ≥ 左、右) 2、堆是用来排序的,其查找效率不高 3、堆,必须是一个完全二叉树 | 1、破坏堆(取出根值,并用完全二叉树的最后一个元素填充根值) 2、恢复堆 | 插入/删除:O(log2n) 构建堆:O(n) 排序:O(nlog2n) | O(1) | N | |||||||||||||||||||||
| 胜者树 - 竞赛树排序 - 其实就是败者树 | O(nlog2n) | |||||||||||||||||||||||||
| 归并排序 | 归并排序 | 1、N个元素,k路归并,趟数m:km = N 2、m = [logkN]向上取整,趟数 | 2路归并: 2个元素/2个块/2个小组,进行1对1比大小,合并成一组,组成新的有序数列 | 2路归并: O(nlog2n),每一趟是O(n),一共 log2n 趟 | O(n),合并需要n个辅助单元 | Y | ||||||||||||||||||||
| 基数排序 分配(收集)排序 | 基数排序 | 适用于 1、n比较大 2、r比较小 3、方便拆,且d比较小 不适用:float、double的实数 | 将n个元素每一个可以拆成d个关键字,每一个关键字有自己的r基数范围 | O( d·(n+r) ) | O(max(r)) | Y | ||||||||||||||||||||
| 外部排序 | 归并排序 | 1、外部排序时间 = 读写外存的时间 + 内部排序所需时间 + 内部归并所需时间 2、优化思路:减少读写外存的趟数:多路归并,可以减少趟数 2路归并需要在内存分配2个输入缓冲区 4路归并需要在内存分配4个输入缓冲区 r个初始归并段,做K路归并 3、内存中任意一个输入缓冲区空了,需要立即从磁盘中加载一个块继续在内存中排序 | 1、生成初始的归并段(让内部有序,每一块都需要读、写一次 2、归并2的次方个“归并段” | |||||||||||||||||||||||
| 优化1: 败者树(选择排序) | ||||||||||||||||||||||||||
| 优化2: 置换-选择排序 + 最佳归并树(哈夫曼树) | 1、置换-选择排序:生成不确定但更长的初始归并段 实际是一个一个先放在CPU输出缓冲区,当缓冲区满了才放回磁盘 2、最佳归并树/哈夫曼树 - 初始归并段的长度 = 每段中的整块数 - m路归并,初始段有x个,则需: (x-1)%(m-1) = u ≠ 0时,需要 m-1-u 个0的虚段 - 读写次数 = 2 · WPL | |||||||||||||||||||||||||










![[论文笔记] Pai-megatron Qwen1.5-14B-CT 后预训练 踩坑记录](https://img-blog.csdnimg.cn/direct/13ad315ebbbd4986a3331d2fd36fc4fd.png)