---

1. 什么是马尔科夫过程

马尔科夫过程（Markov Decision Process, MDP），也称为马尔科夫链（Markov Chain），是指具有马尔科夫性质的过程，而马尔科夫性质指的是该过程中的未来状态仅依赖于当前的状态和行动，与过去的状态序列无关。具体来说，马尔科夫过程满足以下两个性质：

• 无记忆性（Markov Property）：给定当前时刻的状态，未来时刻的状态只依赖于当前时刻的状态，而与过去的状态序列无关。这意味着过程中的状态转移概率只与当前状态有关，与之前的历史状态无关。
• 状态空间可数：马尔科夫过程的状态空间是可数的，即状态集合中的状态数量是有限或可列无穷的。

马尔科夫过程在许多领域都有应用，例如在统计学、信号处理、自然语言处理、金融等领域中都有广泛的应用。

2. 强化学习与MDP的关系

在强化学习中，马尔科夫决策过程是用于建立智能体与环境之间交互过程的重要数学框架，具体而言，强化学习解决的问题就是在一个MDP中找到一个最优的策略，使得智能体在这个策略下获得的累积奖励最大化。

可以将强化学习过程定义为马尔科夫过程的标准数学形式，用一个五元组 $(S,A,R,P,\pi )$ 表示，其中：

1. $S$ 是状态空间集合，包含了所有可能的有效状态；
2. $A$ 是动作空间集合；
3. $R$ 是奖励函数，阶段 $t$ 采取动作的奖励 $r_t=R(s_t,a_t,s_{t+1})$；
4. $P$ 状态转移概率矩阵，其中 $P(s^{\prime }|s,a)$ 是在状态 $s$ 下 采取动作 $a$ 转移到状态 $s^{\prime }$ 的概率；
5. $\pi$ 是智能体在每个状态下采取动作的策略。

其中，对应用强化学习的系统的如下元素做马尔科夫假设：

• 环境的状态转移：即未来的环境状态只与当前的环境状态和当前智能体所采取的动作有关，与过去的状态序列无关；
• 智能体的策略：即智能体在状态 $s$ 处所采取的动作 $a$ 的概率仅与当前状态有关，与其他要素无关，即如下的策略函数：
  $$\pi (a|s)=P(A_t=a|S_t=s)$$
• 状态价值函数：即对一个状态的价值估计只基于当前的状态，而不考虑过去的状态情况，仅评估当前状态下，基于已有策略 $\pi$ 还能获得的累积奖励，具体公式如下：
  $$v_{\pi }(s)={\mathrm{E}}_{\pi }\left(G_t\mid S_t=s\right)={\mathrm{E}}_{\pi }\left(R_t+\gamma R_{t+1}+{\gamma }^2{R}_{t+2}+\dots \mid S_t=s\right)$$
• 动作价值函数：同理，评估一个状态 $s$ 下采取动作 $a$ 的价值，只依赖于当前的状态和动作，与过去的状态和动作无关。

以上部分概念可以通过前文《强化学习基础概念入门》了解。

3. 价值函数的贝尔曼方程¹

在提到马尔科夫决策过程时，经常也会提到贝尔曼方程（Bellman Equation），这是描述马尔科夫决策过程中最优值函数的重要方程。前面提到，不论是状态价值函数还是动作价值函数都是只与当前状态有关，估计的累积价值包括当前阶段的价值和未来阶段的价值，而贝尔曼方程的核心思想就是，将基于当前状态的价值估计和基于下一个状态的价值估计联系起来，形成一个递归方程，作为求解最优价值函数或者动作价值函数的基础。

3.1 状态价值函数的贝尔曼方程

根据上面提到的状态价值函数的表达式，进行如下推导：

$$\begin{array}{rl}{v}_{\pi }(s)& ={\mathrm{E}}_{\pi }\left(R_t+\gamma R_{t+1}+{\gamma }^2{R}_{t+2}+\dots \mid S_t=s\right)\\ & ={\mathrm{E}}_{\pi }\left(R_t+\gamma \left(R_{t+1}+\gamma R_{t+2}+\dots \right)\mid S_t=s\right)\\ & ={\mathrm{E}}_{\pi }\left(R_t+\gamma G_{t+1}\mid S_t=s\right)\\ & ={\mathrm{E}}_{\pi }\left(R_t+\gamma v_{\pi }\left(S_{t+1}\right)\mid S_t=s\right)\end{array}$$

即在 $t$ 时刻的状态估计价值和在 $t+1$ 时刻的状态估计价值满足如下的递推关系（贝尔曼方程）：

$$v_{\pi }(s)={\mathrm{E}}_{\pi }(R_t+\gamma v_{\pi }(S_{t+1})|S_t=s)$$

其中，$R_t$ 是在状态 $s$ 下采取动作后的即时奖励，$\gamma$ 是奖励衰减因子。

3.2 动作价值函数的贝尔曼方程

除了状态价值估计函数 $v_{\pi }(s)$，还有一个动作价值函数 $q_{\pi }(s,a)$，该估计函数考虑了所采取的动作 $a$ 对回报的影响，公式与状态价值函数相似，如下：

$$q_{\pi }(s,a)={\mathrm{E}}_{\pi }\left(G_t\mid S_t=s,A_t=a\right)={\mathrm{E}}_{\pi }\left(R_t+\gamma R_{t+1}+{\gamma }^2{R}_{t+2}+\dots \mid S_t=s,A_t=a\right)$$

同理，可得 $q_{\pi }(s,a)$ 的贝尔曼方程如下：

$$q_{\pi }(s,a)={\mathrm{E}}_{\pi }(R_t+\gamma q_{\pi }(S_{t+1},A_{t+1})|S_t=s)$$

3.3 价值函数递推关系的转换

前面的两种价值函数的贝尔曼方程，尽管呈现了前后阶段的估计价值的递推关系，但是仍是期望表达式，为了最优化动作策略，需要将动作策略 $\pi (a|s)$ 纳入到递推关系当中。

根据动作价值函数 $q_{\pi }(s,a)$ 和状态价值函数 $v_{\pi }(s)$ 的定义，可以得到如下的关系：

$$v_{\pi }(s)=\sum _{a\in A}\pi (a|s)q_{\pi }(s,a)$$

即当前状态的估计价值，是所有动作的估计价值基于策略（概率分布函数） $\pi (a|s)$ 的期望值，即在当前状态和当前策略下，所有动作的估计价值乘以动作的选择概率，求和后得到当前状态的估计价值。

同理，在一个状态 $s$ 下，估计动作 $a$ 的价值即采取了该动作之后，状态转移到下一阶段状态的期望价值，关系如下：

$$q_{\pi }(s,a)=R_t+\gamma \sum _{s^{\prime }\in S}(P_{s{s}^{\prime }}^a{v}_{\pi }(s^{\prime }))$$

即在状态 $s$ 下采取动作 $a$，由于环境的随机因素，状态可能转移到其他的多种状态 $s^{\prime }$，因此评估状态 $s$ 下动作 $a$ 的价值，计算的是下一阶段的状态估计价值的期望，再乘以下一阶段价值（奖励）的衰减因子 $\gamma$。

将上述两个式子彼此代入，得到新的贝尔曼递推关系式，如下：

$$v_{\pi }(s)=\sum _{a\in A}\pi (a|s)(R_t^a+\gamma \sum _{s^{\prime }\in S}(P_{s{s}^{\prime }}^a{v}_{\pi }(s^{\prime })))$$

$$q_{\pi }(s,a)=R_t^a+\gamma \sum _{s^{\prime }\in S}(P_{s{s}^{\prime }}^a\sum _{a^{\prime }\in A}\pi (a^{\prime }|s^{\prime })q_{\pi }(s^{\prime },a^{\prime }))$$

4. 最优价值函数

当我们对价值函数的估计越准确，即策略越有效，则我们决策过程的累积奖励值越大。前面提到，贝尔曼方程是作为求解最优价值函数的基础，通过贝尔曼方程的递推关系，我们可以迭代地求解出最优价值函数，直到算法收敛。

假设在马尔可夫决策过程当中，我们所采取的策略是最优的，表示为 ${\pi }^{\ast }$，它能使得我们在每个阶段的回报都比其他的策略所获回报要高，得到这么一个策略就是强化学习问题所要求的解。但我们很难直接地找到这样地策略，只能在不断的训练中，去比较和学习更优的策略，且对于复杂问题，几乎不可能穷举所有的策略，因此比较得到的最优策略是局部最优的。

比较策略的优劣最直接的方式就是通过比较策略在不同状态下的期望累积奖励大小，其中使得期望累积奖励值达到最大的策略即为最优策略，如下：

$$v_{\ast }(s)=\underset{\pi }{\max }{v}_{\pi }(s)$$

同理，最优动作价值函数的最优策略，如下：

$$q_{\ast }(s,a)=\underset{\pi }{\max }{q}_{\pi }(s,a)$$

假设动作 $a$ 是最优策略所选出的最优动作（这里暂不考虑策略的随机性），则最优状态价值函数和最优动作价值函数之间的关系为：

$$v_{\ast }(s)=\underset{a}{\max }{q}_{\ast }(s,a)$$

$$q_{\ast }(s,a)=R_t^a+\gamma \sum _{s^{\prime }\in S}(P_{s{s}^{\prime }}^a{v}_{\ast }(s^{\prime }))$$

同理，将上述两个式子代入彼此，可以得到最优价值函数，如下：

$$v_{\ast }(s)=\underset{a}{\max }(R_t^a+\gamma \sum _{s^{\prime }\in S}(P_{s{s}^{\prime }}^a{v}_{\ast }(s^{\prime })))$$

$$q_{\ast }(s,a)=R_t^a+\gamma \sum _{s^{\prime }\in S}(P_{s{s}^{\prime }}^a\underset{a‘}{\max }{q}_{\ast }(s^{\prime },a^{\prime }))$$

上述的最优价值函数是在强化学习的迭代训练中不断更新得到的，随着训练场景增多，价值函数不断逼近最优价值函数。

5. MDP计算最优值函数实例²

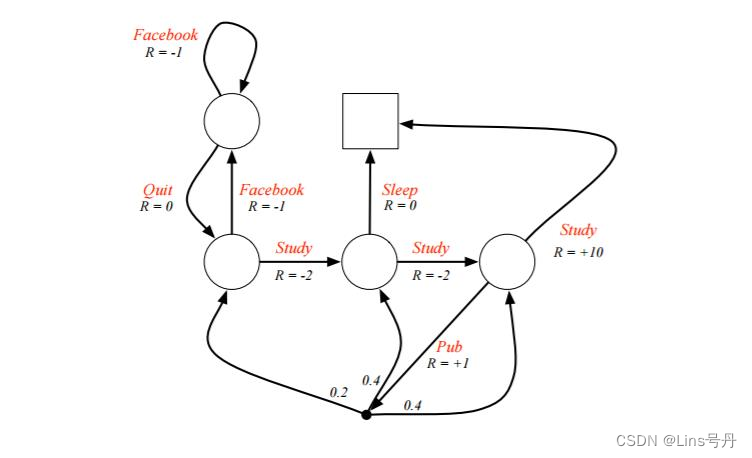
现有一个关于学生开始的马尔科夫决策过程，左上角的圆圈是当前的起始位置（状态），右上角的方框是终点位置（状态）。学生可以采取的动作为下图弧线上的红色字符串，有 $Study,Facebook,Quit,Sleep,Pub$，各个状态下采取动作对应的即时奖励 $R$ 的值在相关弧线上。现需要找到最优的状态价值或动作价值函数，以期能够达成最优策略。

每个非结束状态，都有两种可选择的动作，因此为了方便，我们令初始策略选择每个动作的概率 $\pi (a|s)$ 均为 $0.5$，同时假设奖励衰减因子为 $1$，即初始策略下会考虑当前及未来全量的累积奖励。

这里我们将终点状态的价值设为 $0$，即不论由什么状态通过什么动作直接到达终点，都不增加奖励。接着，定义左上 $s_1$、左下 $s_2$、中下 $s_3$、右下 $s_4$ 四个圆圈的状态价值为 $v_1,v_2,v_3,v_4$，通过以下公式计算各个状态的估计价值（状态价值函数）：

$$v_{\pi }(s)=\sum _{a\in A}\pi (a|s)(R_t^a+\gamma \sum _{s^{\prime }\in S}(P_{s{s}^{\prime }}^a{v}_{\pi }(s^{\prime })))$$

先从起始状态出发，可得如下的方程组：

$$\begin{gathered} v_1=0.5\times (0+v_2)+0.5\times (-1+v_1) \\ {v}_2=0.5\times (-1+v_1)+0.5\times (-2+v_3) \\ {v}_3=0.5\times (-2+v_4)+0.5\times (0+0) \\ {v}_4=0.5\times (10+0)+0.5\times (1+0.2\times v_2+0.4\times v_3+0.4\times v_4) \end{gathered}$$

通过解方程得到 $v_1=-2.3,v_2=-1.3,v_3=2.7,v_4=7.4$，这是在我们规定好价值函数之后求得的状态估计价值，但这不一定是最优价值函数。求最有价值函数的关键在于，求出各个状态的价值，以及每个状态可以采取的动作的估计价值，

假设终点的状态价值仍为 $0$，系统的奖励衰减因子 $\gamma =1$，可得，在（未知）最优策略 $\pi (a|s)$ 下，$q_{\ast }(s_3,sleep)=0,q_{\ast }(s_4,study)=10$。接着利用如下公式：

$$q_{\ast }(s,a)=R_t^a+\gamma \sum _{s^{\prime }\in S}(P_{s{s}^{\prime }}^a\underset{a’}{\max }{q}_{\ast }(s^{\prime },a^{\prime }))$$

得到：

$$\begin{gathered} q_{\ast }(s_3,study)=-2+\max (q_{\ast }(s_4,study),q_{\ast }(s_4,pub)) \\ {q}_{\ast }(s_4,pub)=1+0.2\times \max (q_{\ast }(s_2,facebook),q_{\ast }(s_2,study))+0.4\times \max (q_{\ast }(s_3,study),q_{\ast }(s_3,sleep))+0.4\times \max (q_{\ast }(s_4,study),q_{\ast }(s_4,pub)) \\ {q}_{\ast }(s_2,study)=-2+\max (q_{\ast }(s_3,study),q_{\ast }(s_3,sllep)) \\ {q}_{\ast }(s_2,facebook)=-1+\max (q_{\ast }(s_1,facebook),q_{\ast }(s_1,quit)) \\ {q}_{\ast }(s_1,facebook)=-1+\max (q_{\ast }(s_1,facebook),q_{\ast }(s_1,quit)) \\ {q}_{\ast }(s_1,quit)=-1+\max (q_{\ast }(s_2,study),q_{\ast }(s_2,facebook)) \end{gathered}$$

根据上述方程组求解得到各个状态下的动作价值：

$$\begin{gathered} q_{\ast }(s_3,study)=8 \\ {q}_{\ast }(s_4,pub)=9.4 \\ {q}_{\ast }(s_2,study)=6 \\ {q}_{\ast }(s_2,facebook)=5 \\ {q}_{\ast }(s_1,facebook)=5 \\ {q}_{\ast }(s_1,quit)=6 \end{gathered}$$

接着根据如下公式计算各个状态的估计价值：

$$v_{\ast }(s)=\underset{a}{\max }{q}_{\ast }(s,a)$$

可得：$v_1=6,v_2=6,v_3=8,v_4=10$，即为最终的最优价值估计，基于这些价值估计的策略可得，最优的学习路线为：$s_1\to s_2\to s_3\to s_4\to$ 终点。

---

1. 马尔科夫决策过程(MDP) ：https://www.cnblogs.com/pinard/p/9426283.html ↩︎

2. UCL 强化学习第二章节讲义 https://www.davidsilver.uk/wp-content/uploads/2020/03/MDP.pdf ↩︎