【软件测试之因果图法】

news2024/11/26 1:54:51

【软件测试之判断表法】(蓝桥课学习笔记)

因果图法是一种利用图解法分析输入的各种组合情况，从而设计测试用例的方法，它适合于检查程序输入条件的各种情况的组合。因果图（Cause-Effect-Graphing）提供了把规则转化为判定表的系统化方法，其中“原因”是表示输入条件，“结果”是输入条件经过一系列计算后得到的输出。

因果图实际上是一种数字逻辑电路（一个组合的逻辑网络），但没有使用标准的电子学符号，而是使用了稍微简单点的符号。当然，读者不必要掌握电子学方面的知识，只需要了解逻辑运算符“与”、“或”、“非”即可。

在因果图中使用 4 种符号分别表示 4 种因果关系，如下图所示。用直线连接左右结点，其中左结点 c 表示输入状态（或称原因），右结点 e 表示输出状态（或称结果）。c 和 e 取值都是 0 或者 1，0 表示该条件不出现，1 表示该条件出现。

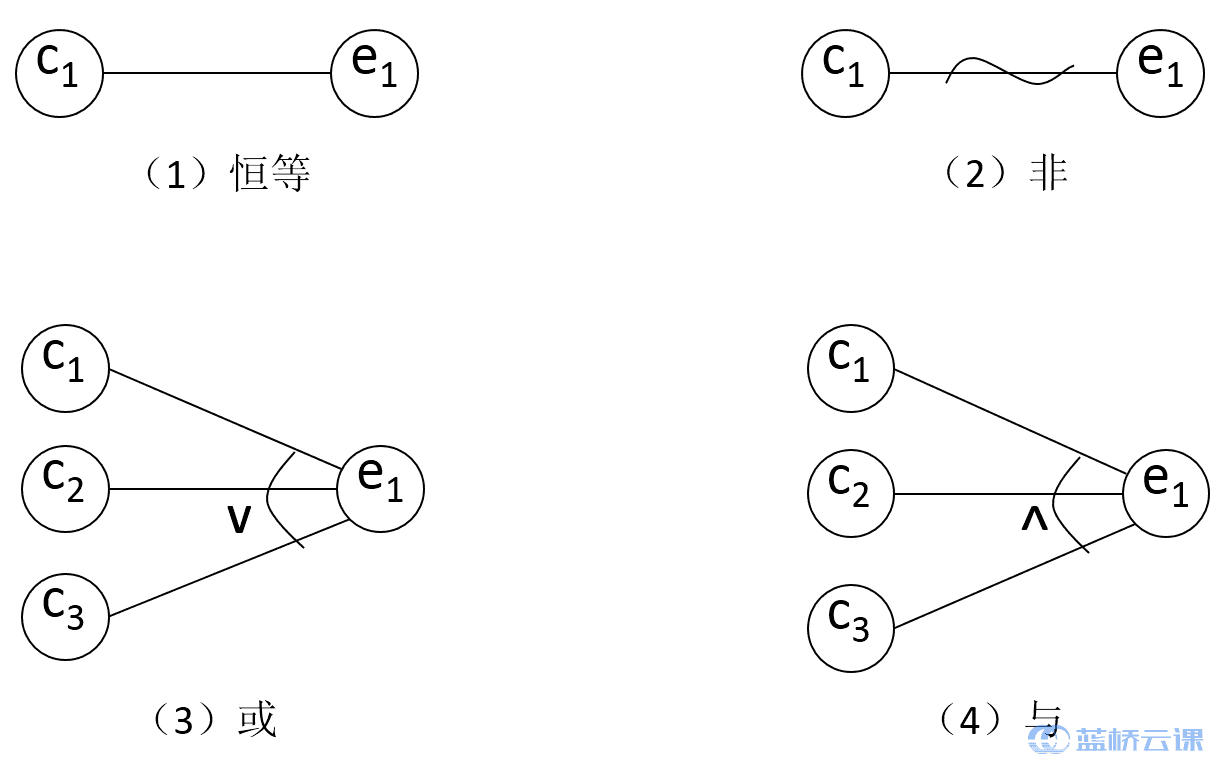
因果图中的四种因果关系

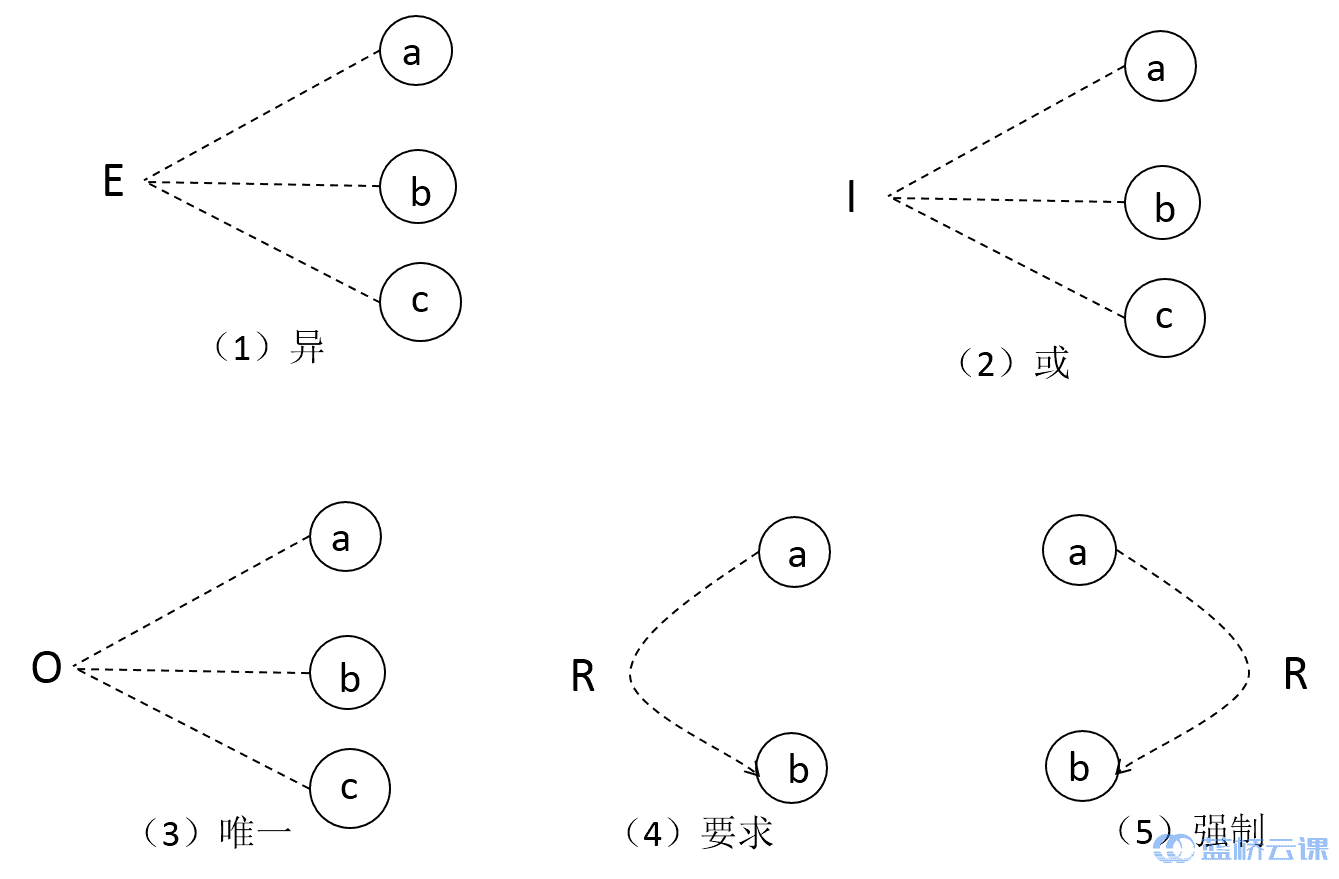
在大多数程序中，有一些输入条件是不可能同时存在的，比如在等价类划分法中的“用户注册”的案例中，用户名的首字符不可能既为字母又为数字，二者为互斥。也就是说输入条件相互之间存在着某些制约关系，称为“约束”。在因果图中，用特定的符号标明这些约束，如下图所示。

因果图中的五种约束关系

E 约束（异、互斥）：a、b、c 中最多有一个可能为 1，也就是 a、b、b 不能同时为 1，输入条件之间为互斥关系。但可以同时为 0。
I 约束（或、包含）：a、b、c 中最少有一个必须是 1，也就是 a、b、c 不能同时为 0，输入条件之间为包含关系。但可以同时为 1。比如程序中的多选按钮。
O 约束（唯一）：a、b、c 中必须有一个且仅有一个为 1。比如程序中的单选按钮。
R 约束（要求）：a 是 1 时，b 必须是 1，a 为 0 时，b 的值不确定。即不可能 a 是 1 时，b 是 0。

以上 4 种是输入条件的约束，输出条件的约束只有一种，就是 M 约束：
M 约束（强制、屏蔽）：若 a 是 1，则 b 强制为 0；若 a 是 0，那么 b 的值不确定。

比如假设在一个注册界面，输入错误的用户名和错误的密码时，都会弹出对应的错误提示。但如果弹出了“用户名错误”的提示，则“密码错误”的提示信息则被屏蔽不会弹出；但如果输入正确的用户名时，那么就不会弹出“用户名错误”的提示信息，但是是否弹出“密码错误”的提示信息则依据密码是否正确而定。

因果图法是从程序规格说明描述中，找出原因（输入条件）和结果（输出或程序状态的改变）。根据原因和结果之间的关系画出关系图，然后转换为特定的判定表的黑盒测试方法。

使用因果图设计测试用例的步骤如下：

某软件的规格说明中对登录名输入包含这样的要求：输入的第一个字符必须是”$”或英文字母，第二个字符必须是一个数字，在此情况下进入第二个窗口；但如果第一个字符不正确，则给出信息 M；如果第二个字符不是数字，则给出信息 N。

【解析】：

分析程序的规格说明，列出原因和结果。如下表所示。

登录的原因和结果分析

将原因和结果之间因果关系用逻辑符号连接起来，得到因果图，如下图所示。

图中 c12为中间节点，是导出结果的进一步原因。

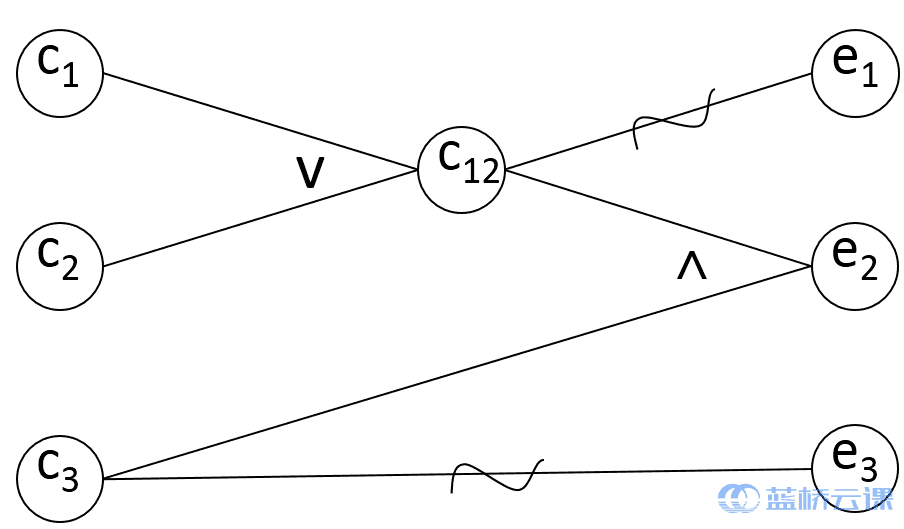
登录的因果图

在因果图上标记约束条件。

因为 c1和 c2不可能同时为 1，即第一个字符不可能既是 c1又是 c2，所以在因果图上对其施加 E 约束，得到具有约束的因果图。如下图所示。

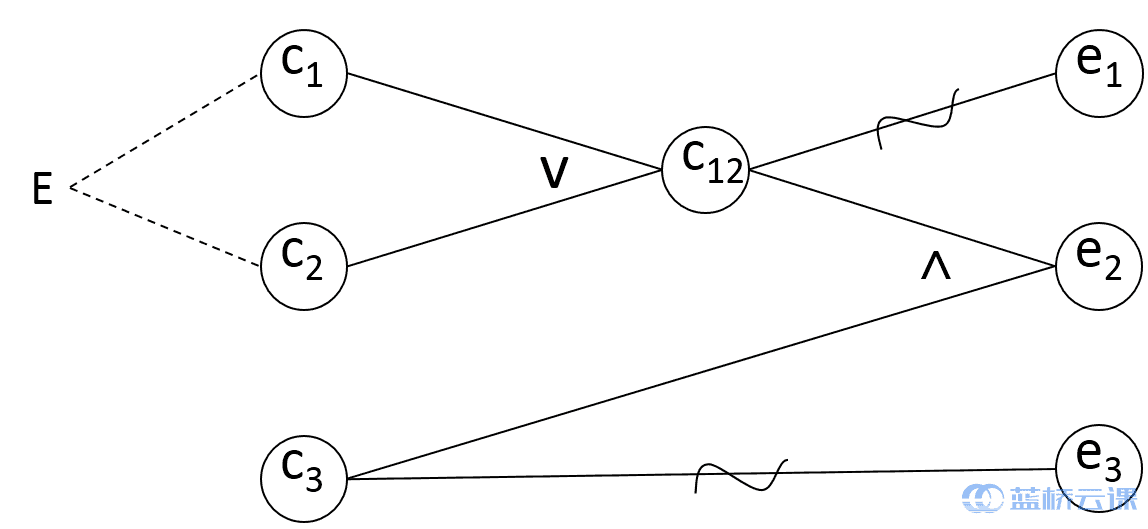
添加约束关系

将因果图转换成判定表，如下表所示：

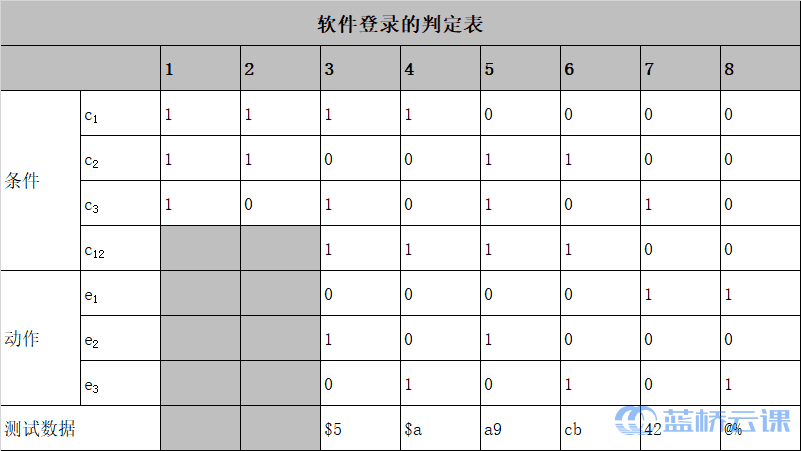
软件登录的判定表

设计测试用例。

表中的前 2 种情况，因为 c1和 c2不可能同时为 1，所以排除。根据判定表，设计出 6 个测试用例，如下表所示。

用例编号	输入数据	预期输出
TC-001	$5	进入第 2 个窗口
TC-002	$a	给出信息 N
TC-003	a9	进入第 2 个窗口
TC-004	cb	给出信息 N
TC-005	42	给出信息 M
TC-006	@%	给出信息 M 和信息 N（是否会弹出信息 N，具体要看程序是否有 M 约束屏蔽发生）