2024年第十四届MathorCup数学应用挑战赛A题解题思路

2024年第十四届MathorCup数学应用挑战赛A题解题思路点击链接加入【2024年第十四届MathorCup数学建模】：

http://qm.qq.com/cgi-bin/qm/qr?_wv=1027&k=Nol416eFZyg4AFPHCZsYfGkLnEnZ8H36&authKey=o9lIFgRfnk2U%2FfYYg1AlFJd5I456CSA2M6nlvJX2qcUockIKuMHj%2BhKMP6RnPeo1&noverify=0&group_code=798702341

添加图片注释，不超过 140 字（可选）

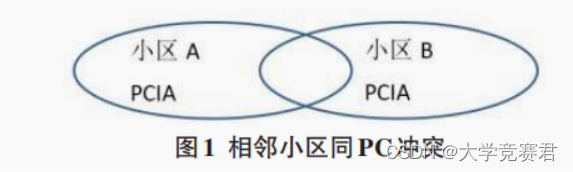
PCI规划原则不冲突原则同（异）频组网时，任意相邻的同频小区不能使用相同的PCI；异频组网时，相邻的异频小区PCI规划不受此原则限制。PCI规划过程有一个基本步骤，即相邻小区不能具有相同的PCI。如果相邻小区具有相同的PCI，则有可能发生 PCI 冲突。在 PCI 冲突的情况下，手机（手机）可能无法获得合适的小区来锁定，这种现象称为PCI冲突。这个问题可以通过在使用相同PCI 的小区之间进行物理分离来解决，以确保手机（手机）永远不会获得相同的PCI。因此应牢记重用距离，PCI冲突会延迟下行链路同步和切换失败。

添加图片注释，不超过 140 字（可选）

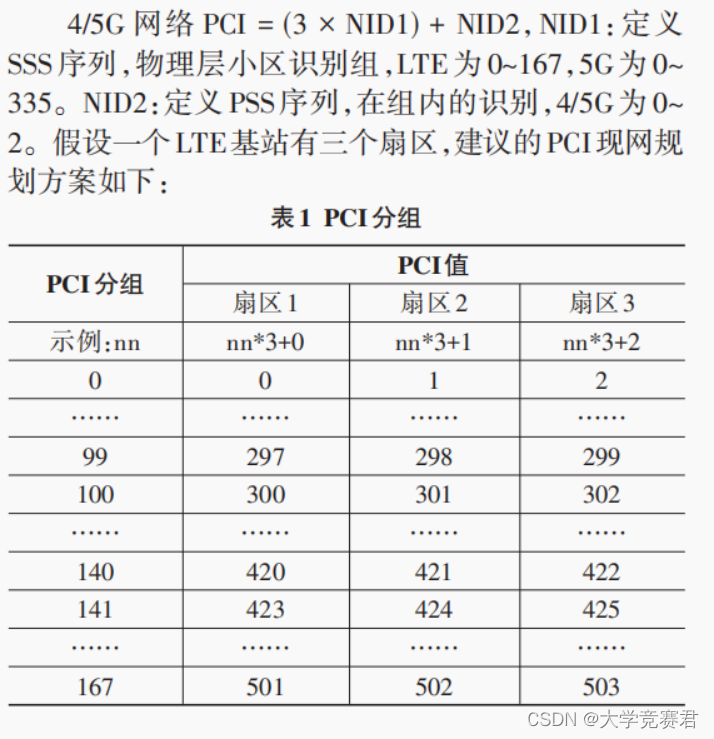
相邻的同频小区的所配置的 PCI 模 3、模 6 不应相同，同时在地理位置上的隔离度足够大，以降低PCI对基站小区的下（上）行参考信号干扰。

添加图片注释，不超过 140 字（可选）

问题1:给这2067个小区重新分配PCI,使得这2067个小区之间的冲突MR数、混淆MR数和模3干扰MR数的总和最少？

问题1的目标是通过重新分配PCI，使得2067个小区之间的冲突MR数、混淆MR数和模3干扰MR数的总和最少。这是一个优化问题，可以采用启发式算法或者数学规划方法来解决。启发式算法如遗传算法、模拟退火等，能够在大规模问题上找到较好的解，而数学规划方法则可以通过确定性的数学模型找到最优解。具体实施时，首先需要根据给定的MR数据计算出冲突矩阵、混淆矩阵和干扰矩阵，然后将这些信息输入到相应的优化算法中，以找到最优的PCI分配方案。

让我们通过一个简化的例子来说明问题。假设我们有6个小区，它们的MR数据如下：

小区A与小区B同频，有3个冲突MR，小区A为主控，小区B为邻区。

小区A与小区C同频，有2个冲突MR，小区A为主控，小区C为邻区。

小区B与小区D同频，有4个冲突MR，小区B为主控，小区D为邻区。

小区C与小区D同频，有1个冲突MR，小区C为主控，小区D为邻区。

根据这些信息，我们可以构建冲突矩阵A如下：

A B C D

A 0 3 2 0

B 3 0 0 4

C 2 0 0 1

D 0 4 1 0

接下来，我们可以根据冲突矩阵A来计算混淆矩阵B。混淆矩阵B表示的是同频小区之间共同邻区的MR数量。在这个例子中，我们可以得到如下的混淆矩阵B：

A B C D

A 0 0 0 0

B 0 0 0 0

C 0 0 0 1

D 0 0 1 0

最后，根据冲突矩阵A和混淆矩阵B，我们可以计算干扰矩阵C。干扰矩阵C表示的是主控小区与其重叠覆盖邻区的MR数量。在这个例子中，我们得到如下的干扰矩阵C：

A B C D

A 0 0 0 0

B 0 0 0 0

C 0 0 0 0

D 0 0 0 0

现在，我们的目标是重新分配PCI，使得这些小区之间的冲突MR数、混淆MR数和模3干扰MR数的总和最少。通过优化算法，我们可以找到最优的PCI分配方案，从而最小化冲突、混淆和干扰的数量。

问题2:考虑冲突、混淆和干扰的不同优先级，给这2067个小区重新分配 PCI，也是考虑这2067个小区之间的冲突、混淆和模3干扰。首先保证冲突的 MR数降到最低，在此基础上保证混淆的MR数降到最低，最后尽量降低模3干扰的MR数。实际网络中，给这2067个小区重新分配PCI，会对这些小区以外的一些距离较近的小区产生影响，也就是这些小区和外围小区之间会产生冲突、混淆和模3干扰的MR数的变化。

问题2需要考虑不同优先级的冲突、混淆和模3干扰，并给这2067个小区重新分配PCI，以最小化这些影响。这是一个更复杂的优化问题，需要综合考虑内部小区之间的冲突、混淆和干扰以及与外部小区之间的影响。

一种解决方法是使用多目标优化算法，如多目标遗传算法或多目标粒子群优化算法。这些算法可以同时优化多个目标函数，以找到一个平衡的解决方案。在这个情况下，我们可以将冲突MR数、混淆MR数和模3干扰MR数分别作为目标函数，并根据其优先级进行加权组合。

为了考虑内部小区对外部小区的影响，我们可以使用仿真方法。通过模拟不同PCI分配方案下的网络性能，可以评估内部小区重新分配PCI对周围小区的影响。这样可以在优化过程中考虑到外部小区与内部小区之间的相互影响，从而得到更全面的解决方案。

综上所述，问题2需要综合考虑多个因素，并采用多目标优化算法和仿真方法来找到最佳的PCI重新分配方案，以最小化冲突、混淆和干扰的影响。

让我们通过一个简化的例子来说明问题2。

假设我们有8个小区，它们之间的冲突、混淆和模3干扰的MR数如下：

冲突MR数：

A B C D E F G H

A 0 3 2 1 0 0 0 0

B 3 0 0 4 0 0 0 0

C 2 0 0 1 0 0 0 0

D 1 4 1 0 0 0 0 0

E 0 0 0 0 0 2 3 1

F 0 0 0 0 2 0 4 2

G 0 0 0 0 3 4 0 3

H 0 0 0 0 1 2 3 0

混淆MR数：

A B C D E F G H

A 0 0 0 0 0 0 0 0

B 0 0 0 0 0 0 0 0

C 0 0 0 0 0 0 0 0

D 0 0 0 0 0 0 0 0

E 0 0 0 0 0 0 0 0

F 0 0 0 0 0 0 0 0

G 0 0 0 0 0 0 0 0

H 0 0 0 0 0 0 0 0

模3干扰MR数：

A B C D E F G H

A 0 0 0 0 0 0 0 0

B 0 0 0 0 0 0 0 0

C 0 0 0 0 0 0 0 0

D 0 0 0 0 0 0 0 0

E 0 0 0 0 0 0 0 0

F 0 0 0 0 0 0 0 0

G 0 0 0 0 0 0 0 0

H 0 0 0 0 0 0 0 0

假设我们将优先级设定为：冲突 > 混淆 > 模3干扰。

我们首先尝试找到一种方案，以最小化冲突MR数为目标。我们可以使用多目标优化算法，如多目标遗传算法，来搜索最佳的PCI分配方案。该算法会尝试不同的PCI分配方案，并根据优先级，选择具有最小冲突MR数的方案。

在得到最小冲突MR数的PCI分配方案后，我们继续优化，以最小化混淆MR数。我们可以在之前的基础上，继续使用多目标优化算法，但这次优化的目标是混淆MR数。算法会尝试调整PCI分配方案，以减少混淆MR数。

最后，我们考虑模3干扰MR数。同样地，我们可以使用多目标优化算法，在之前的基础上继续优化，以最小化模3干扰MR数。

通过这种方式，我们可以得到一个综合考虑冲突、混淆和模3干扰的PCI分配方案，以尽可能减少这些影响。

问题3:给这 2067个小区重新分配PCI，使得所有可能被影响到的小区间的冲突MR数、混淆MR数和模3干扰MR数的总和最少。

解决这个问题需要采用复杂的优化算法，因为要考虑到所有可能被影响到的小区之间的冲突、混淆和模3干扰的情况。一种可能的方法是使用启发式算法，如遗传算法或模拟退火算法，来搜索最佳的PCI分配方案。

首先，我们需要定义一个适应度函数，它将根据PCI分配方案计算出所有可能被影响到的小区之间的冲突、混淆和模3干扰的总和。然后，优化算法将尝试不同的PCI分配方案，并通过评估适应度函数来确定哪个方案最优。

这种问题的规模较大，涉及到2067个小区，因此需要高效的算法和计算资源来求解。实际应用中，可能需要结合各种技术和策略，以找到一个合理的解决方案。

让我们通过一个简化的例子来说明问题3。

假设我们有8个小区，它们之间的冲突、混淆和模3干扰的MR数如下：

冲突MR数：

A B C D E F G H

A 0 3 2 1 0 0 0 0

B 3 0 0 4 0 0 0 0

C 2 0 0 1 0 0 0 0

D 1 4 1 0 0 0 0 0

E 0 0 0 0 0 2 3 1

F 0 0 0 0 2 0 4 2

G 0 0 0 0 3 4 0 3

H 0 0 0 0 1 2 3 0

混淆MR数：

A B C D E F G H

A 0 0 0 0 0 0 0 0

B 0 0 0 0 0 0 0 0

C 0 0 0 0 0 0 0 0

D 0 0 0 0 0 0 0 0

E 0 0 0 0 0 0 0 0

F 0 0 0 0 0 0 0 0

G 0 0 0 0 0 0 0 0

H 0 0 0 0 0 0 0 0

模3干扰MR数：

A B C D E F G H

A 0 0 0 0 0 0 0 0

B 0 0 0 0 0 0 0 0

C 0 0 0 0 0 0 0 0

D 0 0 0 0 0 0 0 0

E 0 0 0 0 0 0 0 0

F 0 0 0 0 0 0 0 0

G 0 0 0 0 0 0 0 0

H 0 0 0 0 0 0 0 0

我们的目标是重新分配PCI，使得所有可能被影响到的小区之间的冲突、混淆和模3干扰的MR数总和最少。

我们可以使用启发式算法来解决这个问题，如遗传算法。该算法将尝试不同的PCI分配方案，并评估每个方案对于总冲突、混淆和模3干扰的MR数的影响。

在遗传算法中，我们首先生成一个初始的PCI分配方案。然后，我们通过交叉、变异等操作来产生新的PCI分配方案。接着，我们计算每个方案的总冲突、混淆和模3干扰的MR数，评估其适应度。根据适应度，我们选择一些优秀的方案，并进行繁殖，以产生下一代的PCI分配方案。重复这个过程，直到达到停止条件，比如达到最大迭代次数或者达到满意的解决方案。

通过这种方式，我们可以找到一个相对优秀的PCI分配方案，以最小化所有可能被影响到的小区之间的冲突、混淆和模3干扰的MR数总和。

问题4:考虑冲突、混淆和干扰的不同优先级，给这2067个小区重新分配 PCI,也是考虑所有可能被影响到的小区间的冲突、混淆和模3干扰。首先保证冲突的MR数降到最低,在此基础上保证混淆的MR数降到最低，最后尽量降低模3干扰的MR数

这个问题涉及到一个复杂的优化过程，需要综合考虑不同优先级的冲突、混淆和干扰的影响，以及各个小区之间的相互影响。以下是一个可能的解决方案：

1.冲突MR数最低化：首先，我们可以尝试寻找一种PCI分配方案，以最小化所有小区之间的冲突MR数。这可以通过启发式算法（如遗传算法、模拟退火算法等）来实现。该算法将尝试不同的PCI分配方案，并评估每个方案对于冲突MR数的影响，选择最优的方案。

2.混淆MR数最低化：在冲突MR数最低化的基础上，我们可以进一步优化PCI分配方案，以最小化所有小区之间的混淆MR数。这也可以通过启发式算法来实现，类似于第一步中所述的方法。

3.模3干扰MR数降低：最后，我们可以尝试调整PCI分配方案，以尽量降低所有小区之间的模3干扰MR数。这可能需要更多的计算资源和时间，因为模3干扰与PCI的模3余数相关，需要考虑更多的约束条件。

整个过程需要综合考虑不同优先级的目标，并根据实际情况进行调整和优化。启发式算法是处理这种复杂优化问题的常用方法，但需要根据具体情况进行参数调整和实验验证，以获得较优的结果。

让我们通过一个简化的例子来说明问题4。

假设我们有8个小区，它们之间的冲突、混淆和模3干扰的MR数如下：

冲突MR数：

A B C D E F G H

A 0 3 2 1 0 0 0 0