面试经典算法系列之二叉树3 -- 二叉树的层序遍历

news2024/11/26 22:45:14

面试经典算法18 - 二叉树的层序遍历

LeetCode.102
公众号：阿Q技术站

问题描述

给你二叉树的根节点 root ，返回其节点值的 层序遍历 。 （即逐层地，从左到右访问所有节点）。

示例 1：

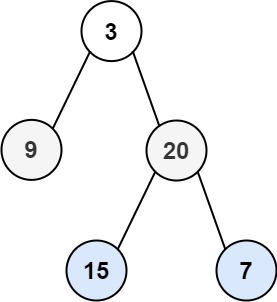
输入：root = [3,9,20,null,null,15,7]
输出：[[3],[9,20],[15,7]]

示例 2：

输入：root = [1]
输出：[[1]]

示例 3：

输入：root = []
输出：[]

提示：

  • 树中节点数目在范围 [0, 2000] 内
  • -1000 <= Node.val <= 1000

思路

递归
  1. 定义一个辅助函数 levelOrderHelper，用来递归遍历二叉树的每一层，并将节点值按层级存储在 result 中。
  2. 辅助函数的参数包括当前节点 root、当前层级 level 和存储结果的二维数组 result。
  3. 如果当前节点为空，则直接返回。
  4. 如果当前层级大于等于 result 的大小，说明需要添加新的一层，因为层序遍历是逐层遍历的。
  5. 将当前节点的值加入到 result 的对应层级中。
  6. 递归遍历当前节点的左子树，层级加一。
  7. 递归遍历当前节点的右子树，层级加一。
  8. 主函数 levelOrder 中调用辅助函数 levelOrderHelper 开始遍历整棵树。
  9. 最后返回存储结果的二维数组 result。
非递归
  1. 创建一个队列 queue 和一个存储结果的二维数组 result。
  2. 将根节点入队。
  3. 循环直到队列为空：
    • 从队列中取出一个节点，将其值存储到当前层级的结果数组中。
    • 如果节点有左子节点，则将左子节点入队。
    • 如果节点有右子节点，则将右子节点入队。
  4. 将当前层级的结果数组加入到最终的结果中。
  5. 继续循环直到队列为空，完成整个二叉树的层序遍历。

图解

  1. 创建一个队列 queue 和一个存储结果的二维数组 result，将根节点入队。

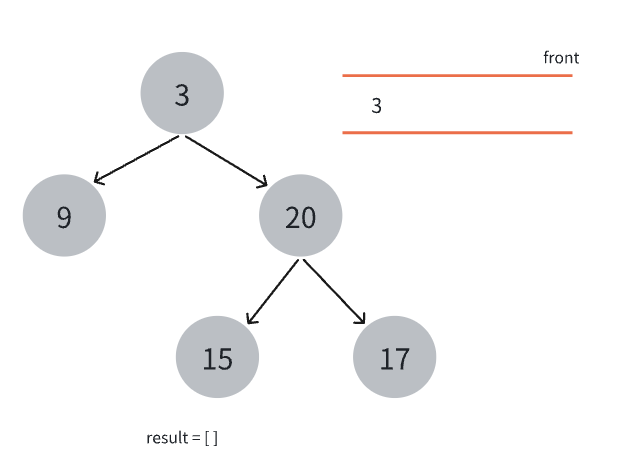
  1. 队列不为空时，新建一个空数组level，用于存储当前层级节点值，然后进行循环打印，循环次数为当前层的节点数，也就是队列的长度。

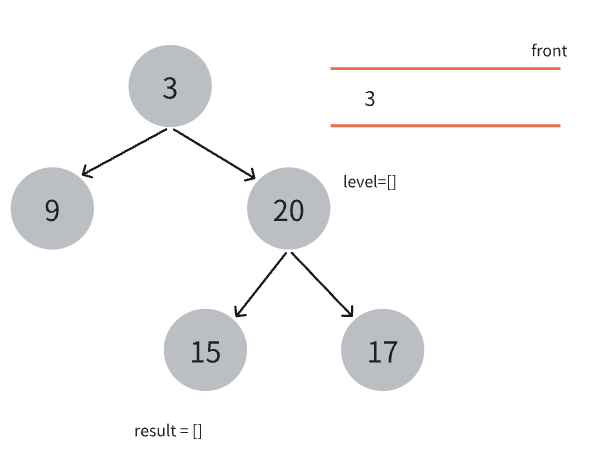
  1. 将队头元素弹出，存入当前层级的数组中。

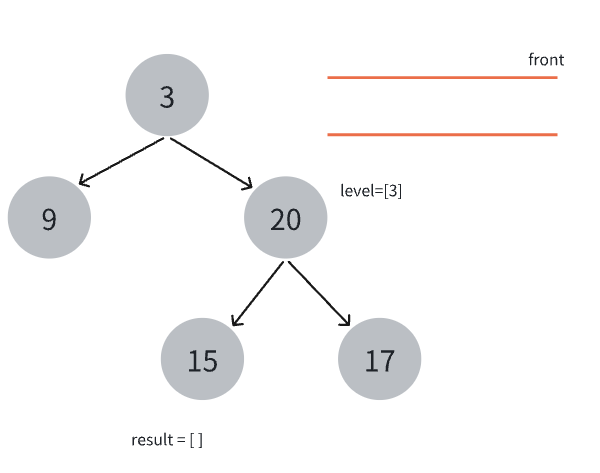
  1. 接着将当前节点的左右节点依次入队（如果有），然后将当前层级的节点值数组加入结果中。

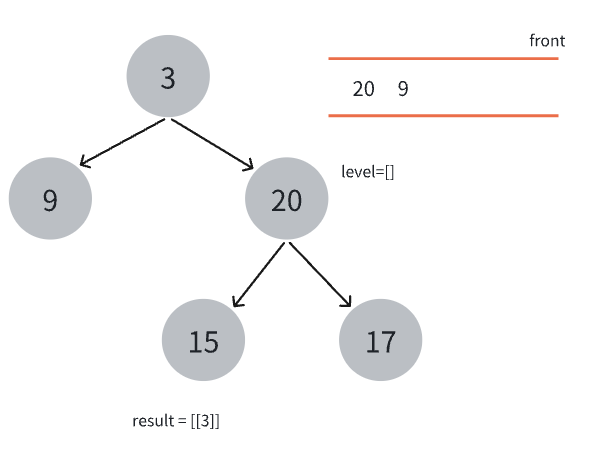
  1. 继续第3步。

  1. 继续第4步。

  1. 继续第3步。

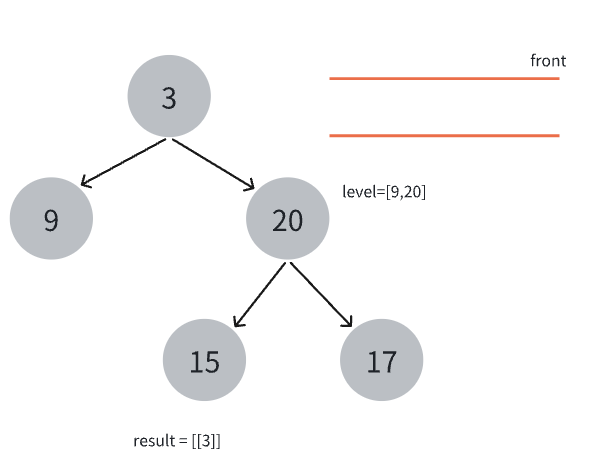
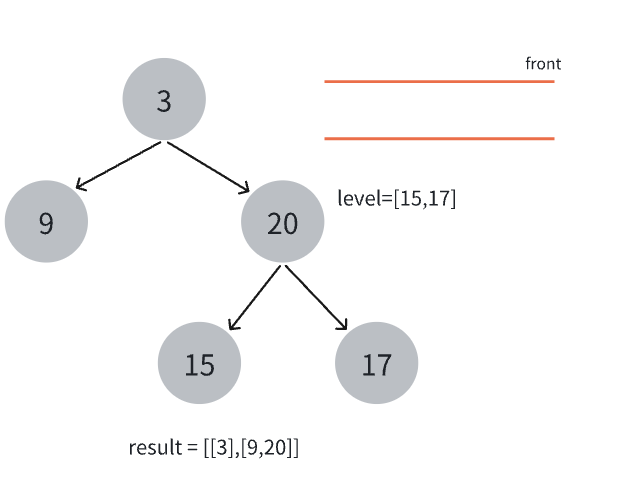
  1. 继续第4步。

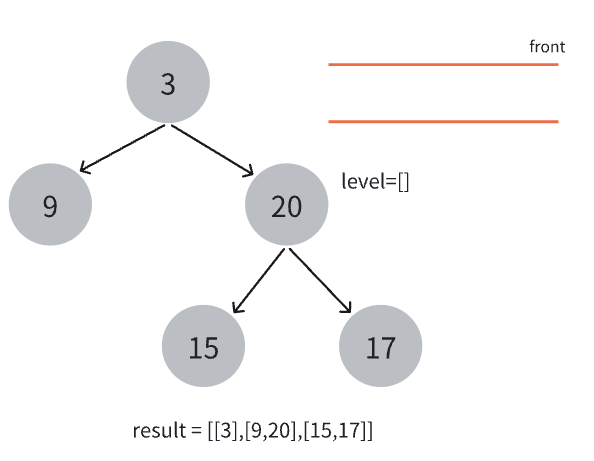
此时，队列为空，退出循环，返回结果集。

参考代码

C++
递归
#include <iostream>
#include <vector>

using namespace std;

// 二叉树节点的定义
struct TreeNode {
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};

// 辅助函数，递归实现层序遍历
void levelOrderHelper(TreeNode* root, int level, vector<vector<int>>& result) {
    if (!root) return;
    
    if (level >= result.size()) {
        result.push_back({});
    }
    
    result[level].push_back(root->val);
    
    levelOrderHelper(root->left, level + 1, result);
    levelOrderHelper(root->right, level + 1, result);
}

// 主函数，返回二叉树的层序遍历结果
vector<vector<int>> levelOrder(TreeNode* root) {
    vector<vector<int>> result;
    levelOrderHelper(root, 0, result);
    return result;
}

// 创建二叉树
TreeNode* createTree(vector<int>& nodes, int index) {
    if (index >= nodes.size() || nodes[index] == -1) {
        return nullptr; // 如果节点为空，则返回nullptr
    }
    TreeNode* root = new TreeNode(nodes[index]); // 创建当前节点
    root->left = createTree(nodes, 2 * index + 1); // 创建左子树
    root->right = createTree(nodes, 2 * index + 2); // 创建右子树
    return root; // 返回当前节点
}

// 销毁二叉树
void destroyTree(TreeNode* root) {
    if (!root) return; // 如果根节点为空，直接返回
    destroyTree(root->left); // 递归销毁左子树
    destroyTree(root->right); // 递归销毁右子树
    delete root; // 删除当前节点
}

int main() {
    // 输入数据，示例二叉树为 {3,9,20,#,#,15,7}
    vector<int> nodes = {3, 9, 20, -1, -1, 15, 7};
    TreeNode* root = createTree(nodes, 0); // 创建二叉树

    // 调用层序遍历函数
    vector<vector<int>> result = levelOrder(root);

    // 输出遍历结果
    for (vector<int> level : result) {
        for (int val : level) {
            cout << val << " ";
        }
        cout << endl;
    }

    // 销毁二叉树
    destroyTree(root);

    return 0;
}
非递归
#include <iostream>
#include <vector>
#include <queue>

using namespace std;

// 二叉树节点的定义
struct TreeNode {
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};

vector<vector<int>> levelOrder(TreeNode* root) {
    vector<vector<int>> result; // 存储结果的二维数组
    if (!root) return result; // 如果根节点为空，直接返回空结果数组

    queue<TreeNode*> q; // 辅助队列，用于层序遍历
    q.push(root); // 将根节点入队

    while (!q.empty()) {
        int size = q.size(); // 当前层级的节点数
        vector<int> level; // 存储当前层级节点值的数组
        for (int i = 0; i < size; i++) {
            TreeNode* node = q.front(); // 获取队头节点
            q.pop(); // 弹出队头节点
            level.push_back(node->val); // 将节点值加入当前层级的数组中
            if (node->left) q.push(node->left); // 将左子节点入队
            if (node->right) q.push(node->right); // 将右子节点入队
        }
        result.push_back(level); // 将当前层级的节点值数组加入结果中
    }

    return result; // 返回层序遍历的结果数组
}

// 创建二叉树
TreeNode* createTree(vector<int>& nodes, int index) {
    if (index >= nodes.size() || nodes[index] == -1) {
        return nullptr; // 如果节点为空，则返回nullptr
    }
    TreeNode* root = new TreeNode(nodes[index]); // 创建当前节点
    root->left = createTree(nodes, 2 * index + 1); // 创建左子树
    root->right = createTree(nodes, 2 * index + 2); // 创建右子树
    return root; // 返回当前节点
}

// 销毁二叉树
void destroyTree(TreeNode* root) {
    if (!root) return; // 如果根节点为空，直接返回
    destroyTree(root->left); // 递归销毁左子树
    destroyTree(root->right); // 递归销毁右子树
    delete root; // 删除当前节点
}

int main() {
    vector<int> nodes = {3, 9, 20, -1, -1, 15, 7}; // 二叉树的层序遍历序列
    TreeNode* root = createTree(nodes, 0); // 创建二叉树
    vector<vector<int>> result = levelOrder(root); // 进行层序遍历
    for (auto& level : result) { // 输出遍历结果
        for (int val : level) {
            cout << val << " ";
        }
        cout << endl;
    }

    destroyTree(root); // 销毁二叉树

    return 0;
}
Java
import java.util.*;

// 二叉树节点的定义
class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;
    TreeNode(int x) { val = x; }
}

public class Main {

    public List<List<Integer>> levelOrder(TreeNode root) {
        List<List<Integer>> result = new ArrayList<>(); // 存储结果的二维数组
        if (root == null) return result; // 如果根节点为空，直接返回空结果数组

        Queue<TreeNode> queue = new LinkedList<>(); // 辅助队列，用于层序遍历
        queue.offer(root); // 将根节点入队

        while (!queue.isEmpty()) {
            int size = queue.size(); // 当前层级的节点数
            List<Integer> level = new ArrayList<>(); // 存储当前层级节点值的数组
            for (int i = 0; i < size; i++) {
                TreeNode node = queue.poll(); // 获取队头节点
                level.add(node.val); // 将节点值加入当前层级的数组中
                if (node.left != null) queue.offer(node.left); // 将左子节点入队
                if (node.right != null) queue.offer(node.right); // 将右子节点入队
            }
            result.add(level); // 将当前层级的节点值数组加入结果中
        }

        return result; // 返回层序遍历的结果数组
    }

    // 创建二叉树
    public TreeNode createTree(Integer[] nodes, int index) {
        if (index >= nodes.length || nodes[index] == null) {
            return null; // 如果节点为空，则返回null
        }
        TreeNode root = new TreeNode(nodes[index]); // 创建当前节点
        root.left = createTree(nodes, 2 * index + 1); // 创建左子树
        root.right = createTree(nodes, 2 * index + 2); // 创建右子树
        return root; // 返回当前节点
    }

    // 销毁二叉树
    public void destroyTree(TreeNode root) {
        if (root == null) return; // 如果根节点为空，直接返回
        destroyTree(root.left); // 递归销毁左子树
        destroyTree(root.right); // 递归销毁右子树
        root = null; // 将当前节点置为null
    }

    public static void main(String[] args) {
        Integer[] nodes = {3, 9, 20, null, null, 15, 7}; // 二叉树的层序遍历序列
        Main main = new Main();
        TreeNode root = main.createTree(nodes, 0); // 创建二叉树
        List<List<Integer>> result = main.levelOrder(root); // 进行层序遍历
        for (List<Integer> level : result) { // 输出遍历结果
            for (int val : level) {
                System.out.print(val + " ");
            }
            System.out.println();
        }

        main.destroyTree(root); // 销毁二叉树
    }
}
Python
from typing import List
from collections import deque

# 二叉树节点的定义
class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

def levelOrder(root: TreeNode) -> List[List[int]]:
    result = [] # 存储结果的二维数组
    if not root:
        return result # 如果根节点为空，直接返回空结果数组

    queue = deque([root]) # 辅助队列，用于层序遍历
    while queue:
        level_size = len(queue) # 当前层级的节点数
        level = [] # 存储当前层级节点值的数组
        for _ in range(level_size):
            node = queue.popleft() # 获取队头节点
            level.append(node.val) # 将节点值加入当前层级的数组中
            if node.left:
                queue.append(node.left) # 将左子节点入队
            if node.right:
                queue.append(node.right) # 将右子节点入队
        result.append(level) # 将当前层级的节点值数组加入结果中

    return result # 返回层序遍历的结果数组

# 创建二叉树
def createTree(nodes: List[int], index: int) -> TreeNode:
    if index >= len(nodes) or nodes[index] is None:
        return None # 如果节点为空，则返回None
    root = TreeNode(nodes[index]) # 创建当前节点
    root.left = createTree(nodes, 2 * index + 1) # 创建左子树
    root.right = createTree(nodes, 2 * index + 2) # 创建右子树
    return root # 返回当前节点

# 销毁二叉树
def destroyTree(root: TreeNode) -> None:
    if not root:
        return # 如果根节点为空，直接返回
    destroyTree(root.left) # 递归销毁左子树
    destroyTree(root.right) # 递归销毁右子树
    root = None # 将当前节点置为None

# 测试代码
nodes = [3, 9, 20, None, None, 15, 7] # 二叉树的层序遍历序列
root = createTree(nodes, 0) # 创建二叉树
result = levelOrder(root) # 进行层序遍历
for level in result: # 输出遍历结果
    print(level)

destroyTree(root) # 销毁二叉树

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1587555.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

虚拟机中，IP地址查询失败怎么办

虚拟机中，IP地址查询失败怎么办

有时候ifconfig查出来的地址是下面这样&#xff0c;只有ipv6 只需要运行下面这两条命令&#xff0c;再次查询即可成功&#xff01; systemctl stop NetworkManagersystemctl start network.service
阅读更多...
Python如何安装第三方模块

Python如何安装第三方模块

cmd窗口中使用pip install命令安装 1、键盘按下win R&#xff0c;然后在输入框中输入cmd&#xff0c;回车&#xff0c;就打开了cmd窗口。 下图的运行框会出现到屏幕左下角。 2、输入下面的命令&#xff0c;回车即可。 pip install xxx # xxx为要安装的模块名 如图所示&…
阅读更多...
RabbitMQ消息模型之Simple消息模型

RabbitMQ消息模型之Simple消息模型

simple消息模型 生产者 package com.example.demo02.mq.simple;import com.example.demo02.mq.util.ConnectionUtils; import com.rabbitmq.client.Channel; import com.rabbitmq.client.Connection;import java.io.IOException;/*** author Allen* 4/10/2024 8:07 PM* versi…
阅读更多...
【论文阅读笔记】Head-Free Lightweight Semantic Segmentation with Linear Transformer

【论文阅读笔记】Head-Free Lightweight Semantic Segmentation with Linear Transformer

莫名地这篇论文我特别难理解&#xff0c;配合代码也食用不了 1.论文介绍 Head-Free Lightweight Semantic Segmentation with Linear Transformer 基于线性Transformer的无头轻量级语义分割 2023年 AAAI Paper Code 2.摘要 现有的语义分割工作主要集中在设计有效的解码器&am…
阅读更多...
MATLAB GUI图形化界面设计计算器

MATLAB GUI图形化界面设计计算器

MATLAB GUI界面设计教程可以帮助用户创建交互式的图形用户界面&#xff0c;以简化与MATLAB程序的交互过程。以下是一个简化的教程&#xff0c;指导你如何进行MATLAB GUI界面设计&#xff1a; 1. 启动GUIDE或App Designer GUIDE&#xff1a;在MATLAB命令窗口中输入guide命令&a…
阅读更多...
锐化空间滤波器--二阶微分图像增强（提高清晰度的另一种方式）

锐化空间滤波器--二阶微分图像增强（提高清晰度的另一种方式）

书上一阶微分的定义可以理解&#xff0c;毕竟这里不死数学上的曲线的概念&#xff0c;而是像素点上的曲线。所以&#xff0c;不同于数学的严格单调递增曲线的导数是大于等于零&#xff0c;这里的严格单调递增曲线&#xff0c;只能是大于零。 至于二阶微分的定义&#xff0c;就…
阅读更多...
Scala实战：打印九九表

Scala实战：打印九九表

本次实战的目标是使用不同的方法实现打印九九表的功能。我们将通过四种不同的方法来实现这个目标&#xff0c;并在day02子包中创建相应的对象。 方法一&#xff1a;双重循环 我们将使用双重循环来实现九九表的打印。在NineNineTable01对象中&#xff0c;我们使用两个嵌套的fo…
阅读更多...
如何使用pgvector为RDS PostgreSQL构建专属ChatBot？

如何使用pgvector为RDS PostgreSQL构建专属ChatBot？

背景 越来越多的企业和个人希望能够利用LLM和生成式人工智能来构建专注于其特定领域的具备AI能力的产品。目前&#xff0c;大语言模型在处理通用问题方面表现较好&#xff0c;但由于训练语料和大模型的生成限制&#xff0c;对于专业知识和时效性方面存在一些局限。在信息时代&…
阅读更多...
Day37:LeedCode 738.单调递增的数字 968.监控二叉树 蓝桥杯 翻转

Day37:LeedCode 738.单调递增的数字 968.监控二叉树 蓝桥杯 翻转

738. 单调递增的数字 当且仅当每个相邻位数上的数字 x 和 y 满足 x < y 时&#xff0c;我们称这个整数是单调递增的。 给定一个整数 n &#xff0c;返回 小于或等于 n 的最大数字&#xff0c;且数字呈 单调递增 。 示例 1: 输入: n 10 输出: 9 思路: 假设这个数是98,…
阅读更多...
三次 Bspline(B样条曲线) NURBS曲线的绘制 matlab

三次 Bspline(B样条曲线) NURBS曲线的绘制 matlab

先来了解几个概念&#xff1a; 1.1 节点向量&#xff1a; B-Spline需要定义曲线的节点向量U&#xff0c;它可以对应到Bezier曲线的参数u。 其元素个数 (m1) 和曲线阶数 k 、控制点个数n满足&#xff1a;m1k1n1 如果U的每段的距离是相等&#xff0c;那么这个B-Spline就被称为均…
阅读更多...
labview中FP.isFrontmost不生效？

labview中FP.isFrontmost不生效？

主GUI界面中调用子GUI程序FP.isFrontmost不生效&#xff1f; 如果主GUI程序使用“floating”,子GUI程序使用default动作&#xff0c;则子GUI无法打开到最前。子GUI程序只能使用“模态”才能置顶。 主GUI程序&#xff1a; 子GUI程序&#xff1a; 改正的方法很简单&#xff0c…
阅读更多...
浙大恩特客户资源管理系统 i0004_openFileByStream.jsp 任意文件读取漏洞复现

浙大恩特客户资源管理系统 i0004_openFileByStream.jsp 任意文件读取漏洞复现

0x01 产品简介 浙大恩特客户资源管理系统是一款针对企业客户资源管理的软件产品。该系统旨在帮助企业高效地管理和利用客户资源，提升销售和市场营销的效果。 0x02 漏洞概述 浙大恩特客户资源管理系统 i0004_openFileByStream.jsp接口处存在任意文件读取漏洞，未经身份验证攻…
阅读更多...
代码随想录 Day17 字符串 | LC344 反转字符串 LC541 反转字符串II 卡码网54替换数字

代码随想录 Day17 字符串 | LC344 反转字符串 LC541 反转字符串II 卡码网54替换数字

一、反转字符串 题目&#xff1a; 力扣344&#xff1a;反转字符串 编写一个函数&#xff0c;其作用是将输入的字符串反转过来。输入字符串以字符数组 s 的形式给出。 不要给另外的数组分配额外的空间&#xff0c;你必须原地修改输入数组、使用 O(1) 的额外空间解决这一问题…
阅读更多...
时间序列突破性创新！与对比学习结合，性能超越SOTA

时间序列突破性创新！与对比学习结合，性能超越SOTA

对比学习可以通过自我监督的方式捕捉时间序列数据中的时间依赖性和动态变化&#xff0c;这使得它特别适合处理时间序列数据&#xff0c;因为时间序列的本质特征就在于其随时间的演变和变化。 因此&#xff0c;相较于传统的时序&#xff0c;基于对比学习的时间序列能够适应更广…
阅读更多...
npm创建Vue3项目

npm创建Vue3项目

npm创建Vue3项目 1 创建Vue项目说明 2 安装3 运行 1 创建Vue项目 创建最新版的Vue项目&#xff0c;已经不推荐使用CLI构建方式了。参考如下即可。 npm create vuelatest如果发现一直动不了&#xff0c;切换网络试一下&#xff0c;个人热点尝试一下。 按下图的选项按需引入自…
阅读更多...
移位寄存器

移位寄存器

移位寄存器是如何工作的&#xff1f; 移位寄存器按照移位方向可分为左移位寄存器、右移位寄存器、双向移位寄存器。图11-15所示为用D触发器构成的4位左移位寄存器。待存数码由触发器F0的输入端D0输入&#xff0c;在移位脉冲作用下&#xff0c;可将数码从高位到低位向左逐步移入…
阅读更多...
如何选择适用于Mac的文件恢复软件？适用于 Mac 的最佳数据恢复软件清单

如何选择适用于Mac的文件恢复软件？适用于 Mac 的最佳数据恢复软件清单

有人会说&#xff0c;我们的数字生活正变得几乎和我们的物理生活一样重要。我们在线工作&#xff0c;将记忆保存在数码照片库中&#xff0c;在信使中交流&#xff0c;并保留各种文档的数字扫描。 每个人都知道备份是必不可少的。建议每天至少同步一个数字备份&#xff08;例如…
阅读更多...
CDHD高创驱动器恢复出厂设置的具体方法演示

CDHD高创驱动器恢复出厂设置的具体方法演示

CDHD高创驱动器恢复出厂设置的具体方法演示 首先，下载并安装高创驱动器的调试软件，有需要的可以从以下链接中获取：高创CDHD伺服调试软件ServoStudio安装包-V2.38.6.30 安装完成后，打开软件，如下图所示， 如下图所示，在左侧找到配置—通信，点击连接， 如下图所示，正常情…
阅读更多...
电力综合自动化系统对电力储能技术的影响有哪些？

电力综合自动化系统对电力储能技术的影响有哪些？

电力综合自动化系统对电力储能技术的影响主要体现在以下几个方面&#xff1a; 提高能源利用效率&#xff1a;电力综合自动化系统通过优化调度和能量管理&#xff0c;可以实现储能设备的有效利用&#xff0c;提高能源利用效率。在电力系统中&#xff0c;储能设备可以有效地平抑风…
阅读更多...
EFcore 6 连接oracle19 WinForm vs2022

EFcore 6 连接oracle19 WinForm vs2022

用EFcore访问Oracle&#xff0c;终于不需要Oracle的什么安装包了&#xff0c;直接在VS2022中就可以轻松搞定。在csdn上看到一哥们的帖子&#xff0c;测试了一下&#xff0c;发现很方便。使用的场景是&#xff1a;VS2022中EFcore6。经过测试&#xff0c;同 Navicat Premium 16比…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023