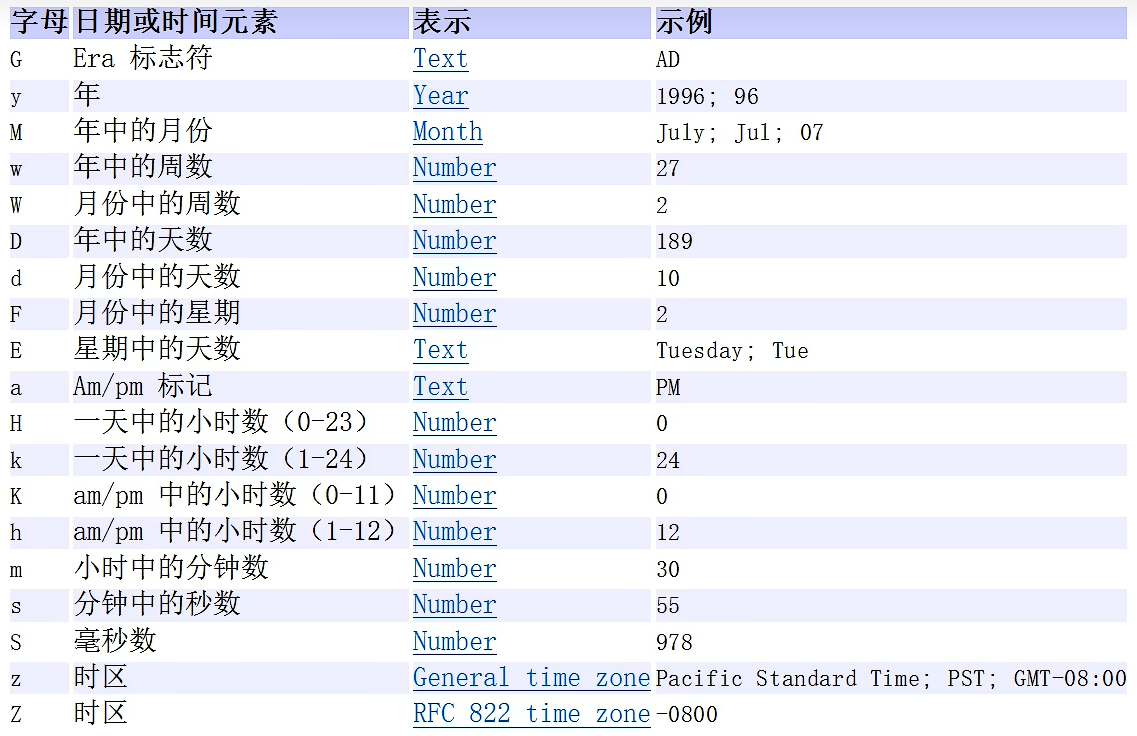
递归算法实例应用（一）

递归简笔

递归和普通函数调用一样，都是通过函数栈实现。

以斐波那契数列递归调用为例
斐波那契数列递归调用图示

递归时函数调用栈的进栈、出栈过程可以由上述图示直观的体现出来，

因此可以得出递归的几个作用：

1）替代多重循环

2）解决以递归形式或潜在以递归形式定义的问题

3）将问题规模分解，分解为规模更小的子问题进行求解

$\cdots\cdots\cdots$

Hanoi (Simple)

Description

古代有一座汉诺塔，塔内有3个座A、B、C，A座上有n个盘子，盘子大小不等，大的在下，小的在上，如图4-1所示。有一个和尚想把这n个盘子从A座移到C座，但每次只能移动一个盘子，并且在移动过程中，3个座上的盘子始终保持大盘在下，小盘在上。在移动过程中可以利用B座来放盘子。要求输出移动的步骤。

Input

汉诺塔内的盘子个数 $\le n \le 64）$ 。

Output

输出移动的步骤，每行一步，如从A座移动到C座，输出“A->C”。

Sample Input

Sample Output

A->C
A->B
C->B
A->C
B->A
B->C
A->C

这是最简单的Hanoi问题，其余进阶版的Hanoi问题均由此发展而来。

该题是一个非常明显的以递归形式定义的问题，即：

要把A座上的盘子移动到C座的问题分解为三步：

把A座上的n-1个盘子移动到B座作为中转，且以C座作为中转；
把A座剩余的一个盘子移动到C座；
再把B座的n-1个盘子移动到C座，且以A做作为中转。

这样就把原问题的规模减小至n-1，通过逐层递归可以将问题规模减少至1，此时就可以通过直接将A座盘子移动到C座完成，在逐步向上返回至上一层调用函数，直至问题规模n完成求解。

由上述分析显然可知，当问题规模减少至1时为终止条件，此时应将A座盘子移动到C座上，即输出A->C，同时结束本次递归，返回至上一层递归函数处。

所以主函数及递归段代码为：

void Hanoi(int n, char A, char B, char C) {
    if (n == 1) {//问题规模到达1时为递归终止条件
        printf("%c->%c\n", A, C);
        return;
    }
    //将A座n-1个盘子移动至B座，同时以C座作为中转
    Hanoi(n - 1, A, C, B);
    //将A座第n个盘子移动至C座
    printf("%c->%c\n", A, C);
    //将B座的n-1个盘子移动至C座，同时以A座作为中转
    Hanoi(n - 1, B, A, C);
}

int main() {
    int n;
    scanf("%d",&n);
    //将n层汉诺塔中A座移动到C座，同时以B座作为中转
    Hanoi(n, 'A', 'B', 'C');
}

N Queens

Description

The eight queens puzzle is the problem of putting eight chess queens on an 8 × 8 chessboard such that none of them is able to capture any other. The puzzle has been generalized to arbitrary n × n boards. Given n, you are to find a solution to the n queens puzzle.

Input

The input contains multiple test cases. Each test case consists of a single integer n between 8 and 300 (inclusive). A zero indicates the end of input.

Output

For each test case, output your solution on one line. The solution is a permutation of $\{1,2,\cdots,n \}$ . The number in the ith place means the ith-column queen in placed in the row with that number.

Sample Input

Sample Output

2 4 1 3
3 1 4 2

为方便理解题意，依样例输入输出可以画出四皇后图例：

题中要求皇后不能在同一行、同一列、同一对角线。

不难想到可以通过枚举所有可能的皇后状态来暴力求解，比如当 N = 4 时，可以通过4重循环嵌套来实现枚举。

但是该问题的问题规模N是一个不确定是整数，N重循环嵌套就无法实现，所以可以考虑采用递归来替代多重循环。

分析至此，本题的递归又自然而然的引出了回溯法这一基本算法理念，当不断的枚举每一种可能的状态时，若发生了与规则矛盾的错误，则应立即终止本层递归，回溯至上层，进行下一状态的枚举。

准备工作：

而如何枚举全每一种可能的状态，有多种方法，如按行枚举、按列枚举、按对角线枚举等，本文采用按行枚举进行操作。所以递归函数的形参就呼之欲出：int n，因为我们假定递归模型是按行进行枚举的，所以n用于表示0~n-1行皇后已经摆好，当前递归函数为处理第n行皇后的位置。

所以应再设置一个PosOfQueen的一维数组，其下标表示棋盘的第i行，其值PosOfQueen[i]表示第i行皇后摆放在第几列，如PosOfQueen[2]=4,表明第2行（棋盘的第3行）皇后摆放第4列（棋盘的第五列）。

算法逻辑：

其中，NofQueen表示N皇后中的规模N

若本层递归参数n==NofQueen，即表明N皇后已经摆放正确，所以此时为该问题的递归终止条件，应输出问题的一个解。

代码描述为：

if (n == NofQueen) {//N个皇后已经摆好
    for (i = 0; i < NofQueen; ++i) {
        printf("%d ", PosOfQueen[i] + 1);//输出每一行皇后摆在哪一列
    }
    printf("\n");
    return;
}

若本层递归不为第N行，则应处理第n行的皇后，即确定第n行皇后的摆放位置。所以应从0~NofQueen-1枚举所有可能的摆放位置。假设以i枚举时行递增变量

枚举时，首先，与前0~n-1行已经确定位置的n个元素进行比较，判断是否同行、同列、同对角线
- 同行判定：由于是按行遍历每行确定一个元素的位置，所以不可能有元素是同行。
- 同列判定：PosOfQueen[j]数组的值表明第j行皇后摆放在第几列，所以同列判断较为简单，代码描述为：
```
PosOfQueen[j] == i
```
- 同对角线判定：
  
  j=1 j=2 j=3 j=4
  i=1 (1,1) (1,2) (1,3) (1,4)
  i=2 (2,1) (2,2) (2,3) (2,4)
  i=3 (3,1) (3,2) (3,3) (3,4)
  i=4 (4,1) (4,2) (4,3) (4,4)
  上表描述为4*4的棋盘，其中
  1. 主对角线
    - 主对角线1：(1,1)、(2,2)、(3,3)、(4,4)
    - 主对角线2：(1,2)、(2,3)、(3,4)
    - 主对角线3：(2,1)、(3,2)、(4,3)
    - 主对角线4：(1,3)、(2,4)
    - 主对角线x: …、…
      
      观察发现，每一个主对角线上各个元素的行列下标差的绝对值均相等，即 $∣ i - j ∣$ 均相等。
      
      如：主对角线2中， $∣1 - 2∣ = ∣2 - 3∣ = ∣3 - 4∣ = 1$
      
      主对角线3中， $∣2 - 1∣ = ∣3 - 2∣ = ∣4 - 3∣ = 1$
  2. 副对角线
    - 副对角线1：(1,4)、(2,3)、(3,2)、(4,1)
    - 副对角线2：(1,3)、(2,2)、(3,1)
    - 副对角线3：(2,4)、(3,3)、(4,2)
    - 副对角线4：(1,2)、(2,1)
    - 副对角线x: …、…
      
      观察发现，每一个副对角线上各个元素的行列下标之和均相等。即 $i + j$ 均相等。
      
      如：副对角线2中， $1 + 3 = 2 + 2 = 3 + 1 = 4$ 。
      
      副对角线3中， $2 + 4 = 3 + 3 = 4 + 2 = 6$ 。
综上所述，可将同行（忽略）、同列、同主副对角线判定代码合并为：
```
if (PosOfQueen[j] == i || abs(PosOfQueen[j] - i) == abs(n - j)) {
    //同行不必判断，判断是否同列、同主对角线、同副对角线。
    break;//规则冲突,测试下一可能位置，再通过剪枝来减少不必要的开销
}
```
其次，若与前0~n-1行判断是否同行、同列、同对角线完成后，与题目规则不冲突，则将第n行皇后摆放在当前枚举状态下的的可能位置i处，随后进行下一行皇后位置的确定，即进入下一层递归中。

代码描述如下：
```
if (j == n) {//当前轮次枚举中位置i与前0~n-1行合法性判断均通过，当前位置合法
    PosOfQueen[n] = i;//将第n个皇后摆放在位置i
    NQueen(n + 1);//递归调用函数，处理n+1行皇后位置摆放问题
}
```
至此，递归函数已经完成，在递归函数中，第一步中的if语句为递归终止点，同时也是回溯法成功找到解时的判定条件。在第二步中，通过逐步尝试每一个可能位置的，并通过回溯保证本次递归是在上一层递归函数正确的条件下进行的枚举尝试，不断穷尽解集二叉树中的所有分支。

	j=1	j=2	j=3	j=4
i=1	(1,1)	(1,2)	(1,3)	(1,4)
i=2	(2,1)	(2,2)	(2,3)	(2,4)
i=3	(3,1)	(3,2)	(3,3)	(3,4)
i=4	(4,1)	(4,2)	(4,3)	(4,4)

代码整合：

综上，代码可整合为：

void NQueen(int n) {//在0~n-1行的皇后已经摆好的情况下，摆第n行及其之后的皇后
    int i, j;
    if (n == NofQueen) {//N个皇后已经摆好
        for (i = 0; i < NofQueen; ++i) {
            printf("%d ", PosOfQueen[i] + 1);//输出每一行皇后摆在哪一列
        }
        printf("\n");
        return;
    }
    for (i = 0; i < NofQueen; ++i) {
        for (j = 0; j < n; ++j) {//每一轮for循环均回溯至i行处，因此可以穷尽所有可能解的二叉树的叶子结点
            if (PosOfQueen[j] == i || abs(PosOfQueen[j] - i) == abs(n - j)) {
                //同行不必判断，判断是否同列、同主对角线、同副对角线。
                break;//规则冲突,test next pos  再通过剪枝来减少不必要的开销
            }
        }
        if (j == n) {//与前0~n-1行合法性判断均通过，当前位置合法
            PosOfQueen[n] = i;//将第n个皇后摆放在位置i
            NQueen(n + 1);//递归调用函数，处理n+1行皇后位置摆放问题
        }
    }
}

int NofQueen;           //N皇后的N
int PosOfQueen[100];    //棋盘数组，下标表示行号，值表示列号

int main() {
    scanf("%d", &NofQueen);
    NQueen(0);//从棋盘第0层开始逐层递归解决
}