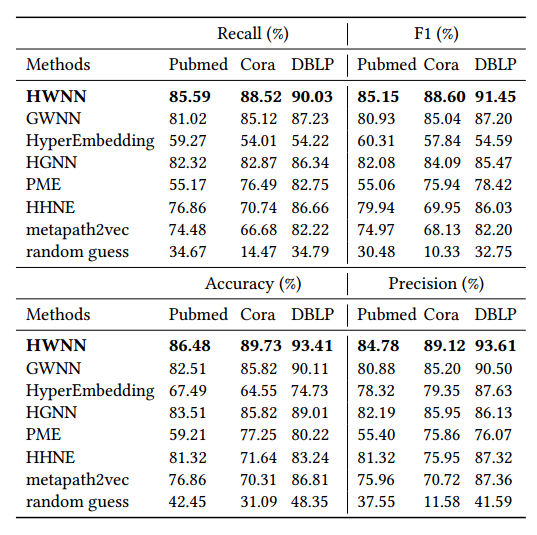
灵能传输

友情链接：灵能传输

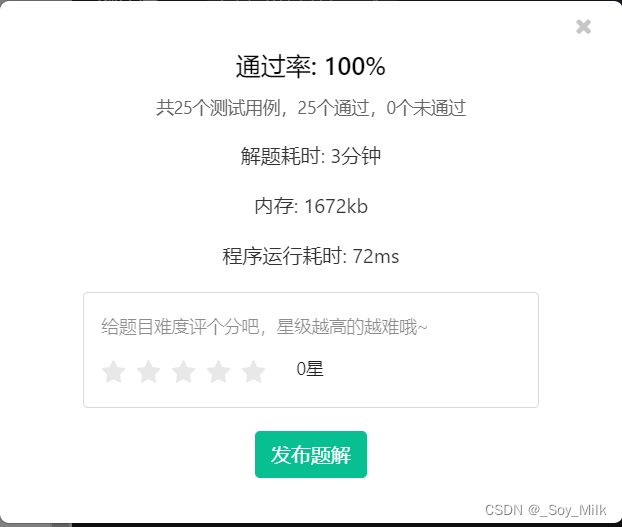
题目：

输入样例：

3
3
5 -2 3
4
0 0 0 0
3
1 2 3

输出样例：

3
0
3

思路：

题目大意：给出一个数组，每次选择数组中的一个数（要求不能是第一个数与最后一个数），如果这个数是一个正数，就将这个数减去自身两次，并且将相邻的两个数分别加上这个数一次，如果这个数是负数，就将这个数减去自身两次，并且将相邻的数加上这个负数两次，（本质上第二种情况与第一种情况一样，因为减去负数相当于加上这个负数的绝对值），使用公式表述为：$a_{i-1}+=a_i{a}_{i+1}+=a_i{a}_i-=2a_i$，并且记住选择的i不能是第一个数或最后一个数。

具体思路：

通过尝试可知，公式与每一个数的前缀和有极大的关系，举例：对于数组5 -2 3 4而言，其前缀和为5 3 6 10，如果选择的是-2，那么原数组的值会变为：3 2 1 4，变化后的数组前缀和为：3 5 6 10，相当于将原数组的前缀和中的第一个位置与第二个位置进行了交换，再看还是对于数组5 -2 3 4而言，如果选择的是3，那么原数组的值会变为5 1 -3 7，对应的前缀和为5 6 3 10，相当于对原数组的前缀和数组的第二个位置与第三个位置进行了交换。下图为更直观的理解：

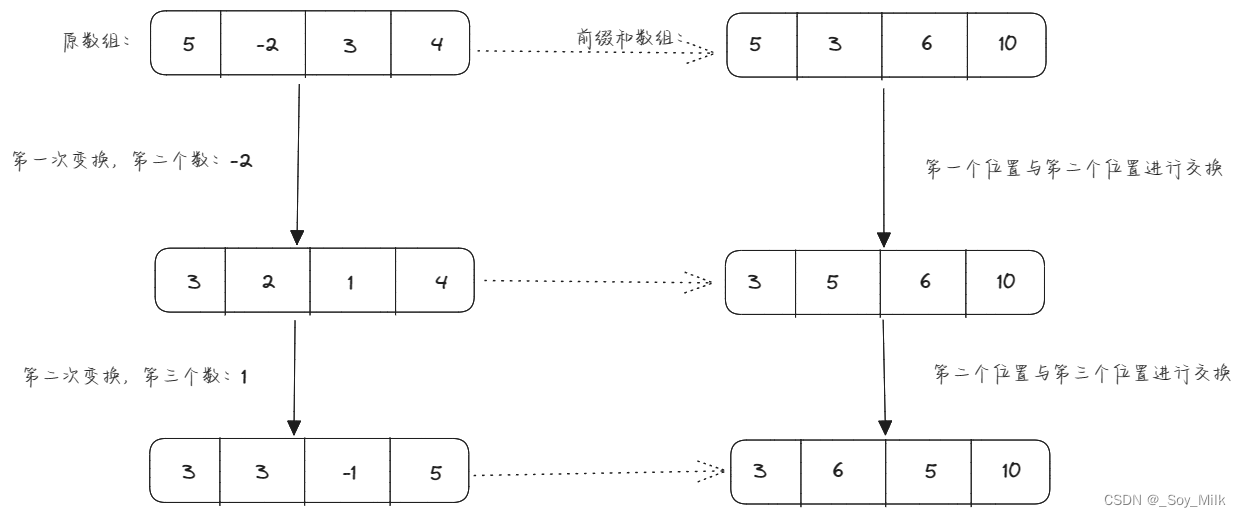
由此我们可以得出一个规律：如果对某一个位置i进行操作，相当于对前缀和数组中i与i - 1位置的值进行交换。其中：1 < i < n。

这样我们就可以得出一个简单的解决方案了，题目要求的是使原数组中数值的绝对值的最大值最小化，一个简单的思路是对前缀和数组进行排序，因为这样可以保证相邻两个前缀和数值的差值最小，这样就保证了原数组中的数值的最大值最小化。

但是题目还有一个条件，就是不能对第一个位置和最后一个位置进行操作，如果直接对前缀和数组（前缀和数组表示为：$S$）进行排序（包含了$S_0$和$S_n$），那么就违反了题目的要求。我们这样思考：如果对$a_1$（原数组用$a$表示）进行操作，那么对应的前缀和变化是交换$S_0$和$S_1$（其中$S_0=0$ ），如果对$a_n$进行操作，那么对应的前缀和数组的变化是交换$S_n$和$S_{n-1}$，为了不使$S_0$和$S_n$移动，我们这两个数进行移动，我们需要让起点仍然是因为$S_0$和$S_n$，但为了使相邻两个值之间的差值最小，我们需要使用一些策略：如从$S_0$的位置进行步长为2向前进行取值正序填充到一个新的数组中去并且进行标记，在$S_n$的位置也进行步长为2向后进行取值，逆序（即：从新数组的最后一个位置开始进行填充）填充到一个新的数组中去并且进行标记，最后从头开始遍历排序后的前缀和数组，将还未标记的值按顺序一次填充到新的数组的空余位置。

还有一个问题：$S_0$如果大于$S_n$该如何解决？

对于这种情况：我们只需要在查找$S_0$和$S_n$的位置的时候将$S_0$和$S_n$的位置进行交换即可，这样就变为了$S_n$向前进行步长为2的取值，$S_0$向后进行步长为2的移动。下图为一个直观的理解：

记得要使用long long数据类型，因为int类型的数据最大在$10^9$左右，而题目要求的$a_i$的值小于等于$10^9$，其前缀和数组的值可能会超过int的存储容量。

代码：

#include<bits/stdc++.h>
using namespace std;

typedef long long ll;
void solve(){
	int n; cin>>n;
	vector<ll> A(n + 1, 0);
	vector<ll> S(n + 1, 0);
	for(int i = 1;i <= n;i ++){
		cin>>A[i];
		S[i] += S[i - 1] + A[i];
	}
	
	// 记录S中的第一个位置与最后一个位置
	ll front = S[0];
	ll end = S[n];
	if(front > end) swap(front, end);
	// 对前缀和数组进行顺序排序
	sort(S.begin(), S.end());   // 排序的时候包含了第0个位置的数 
	
	// 找到原来S数组的第一个位置和最后一个位置的数在排序后的数组中的下标
	for(int i = 0;i <= n;i ++){
		if(S[i] == front){
			front = i;
			break;
		}
		
	}
	for(int i = n;i >= 0;i --){   // 这里遍历也可以从0开始到n结束
		if(S[i] == end){
			end = i;
			break;
		}
		
	}

	vector<ll> ans(n + 1, 0);
	// 设定标记数组
	vector<ll> cnt(n + 1, 0);
	ll frontidx = 0;
	ll endidx = n; 
	// 从idxf向前进行找
	for(int i = front;i >= 0;i -= 2){
		ans[frontidx++] = S[i];
		cnt[i] = 1;
	}
	// 从idxe向后进行找 
	for(int i = end;i <=n ;i += 2){
		ans[endidx --] = S[i];
		cnt[i] = 1;
	}
	// 将剩下的数进行填充 
	for(int i = 0;i <= n;i ++){
		if(!cnt[i]){
			ans[frontidx++] = S[i];
		}
	}
	
	// 从ans数组中找到相邻两个数之间的最小的值
	ll tans = 0;
	for(int i = 1;i <= n;i ++){
		tans = max(tans, abs(ans[i] - ans[i - 1]));
	}
	cout<<tans<<endl;
	return ;
} 

signed main(){
	ios::sync_with_stdio(0);
	cin.tie(0);
	int t = 1; cin>>t;  // t组询问 
	while(t--){
		solve();
	}
	return 0;
}