目录
简介
设置
卷积
演变
测试逆卷积层
图像分类
获取 CIFAR10 数据集
数据可视化
卷积神经网络
逆向传播神经网络
比较
损失图和准确率图
可视化卷积核
结论
政安晨的个人主页:政安晨
欢迎 👍点赞✍评论⭐收藏
收录专栏: TensorFlow与Keras机器学习实战
希望政安晨的博客能够对您有所裨益,如有不足之处,欢迎在评论区提出指正!
本文目标:深入研究特定位置和渠道无关的“内卷”核函数。
简介
卷积是大多数现代计算机视觉神经网络的基础。卷积核具有空间无关性和通道特定性。因此,它无法适应不同空间位置的不同视觉模式。除了与位置相关的问题,卷积的作用范围也给捕捉远距离空间相互作用带来了挑战。
为了解决上述问题,Li 等人在《卷积》一书中重新思考了卷积的特性:Inverting the Inherence of Convolution for VisualRecognition》一书中重新思考了卷积的特性。作者提出了 "卷积内核"(involution kernel),它具有位置特定性和通道无关性。由于这种操作具有特定位置的性质,作者认为自我注意属于内卷的设计范例。
本示例介绍了内卷核,比较了两种图像分类模型(一种是卷积模型,另一种是内卷模型),并尝试将其与自我注意层相提并论。
设置
import os
os.environ["KERAS_BACKEND"] = "tensorflow"
import tensorflow as tf
import keras
import matplotlib.pyplot as plt
# Set seed for reproducibility.
tf.random.set_seed(42)卷积
在计算机视觉中,卷积是一种重要的操作,用于图像处理和特征提取。卷积通过将一个滤波器或核与输入图像进行逐像素的计算,生成一个新的输出图像。
卷积操作与图像处理中常用的滤波操作类似,滤波器在图像上滑动并与图像的局部区域进行点乘,然后将乘积相加得到新的像素值。这个过程可以看作是将滤波器与图像进行卷积计算。
卷积操作的一个重要特性是它具有局部感知性。即卷积运算只计算滤波器与图像窗口内像素的乘积和,并将结果相加。这样的操作可以有效地提取图像的局部特征,例如边缘和纹理等。
卷积在计算机视觉中有广泛的应用。它可以用于图像增强、边缘检测、特征提取、目标检测和图像分类等任务。卷积神经网络(Convolutional Neural Network,CNN)是计算机视觉领域中最重要的算法之一,它借鉴了卷积操作的思想,并在深度学习中取得了很大的成功。
总之,卷积是计算机视觉中的一种重要操作,它能够提取图像的局部特征,并被广泛应用于图像处理和特征提取任务中。
卷积是计算机视觉深度神经网络的支柱。要理解卷积,就必须先谈谈卷积操作。

考虑一个维数为 H、W 和 C_in 的输入张量 X。我们取一组 C_out 卷积核,每个核的形状为 K、K、C_in。通过对输入张量和卷积核进行乘加运算,我们得到一个维数为 H、W、C_out 的输出张量 Y。
在上图中,C_out=3。这使得输出张量的形状为 H、W 和 3。我们可以注意到,卷积核并不依赖于输入张量的空间位置,因此它与位置无关。另一方面,输出张量中的每个通道都基于特定的卷积滤波器,这使得它具有特定通道的特性。
演变
我们的想法是让操作既能针对特定位置,又能与通道特定性无关。要实现这些特定属性是一项挑战。如果使用固定数量的卷积核(针对每个空间位置),我们将无法处理可变分辨率的输入张量。
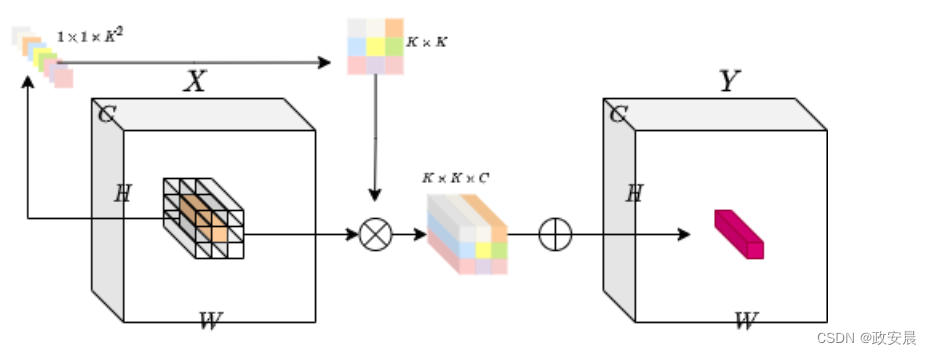
为了解决这个问题,咱们考虑根据特定的空间位置生成每个内核。通过这种方法,我们应该可以轻松处理变分辨率输入张量。下图提供了这种内核生成方法的直观图。
class Involution(keras.layers.Layer):
def __init__(
self, channel, group_number, kernel_size, stride, reduction_ratio, name
):
super().__init__(name=name)
# Initialize the parameters.
self.channel = channel
self.group_number = group_number
self.kernel_size = kernel_size
self.stride = stride
self.reduction_ratio = reduction_ratio
def build(self, input_shape):
# Get the shape of the input.
(_, height, width, num_channels) = input_shape
# Scale the height and width with respect to the strides.
height = height // self.stride
width = width // self.stride
# Define a layer that average pools the input tensor
# if stride is more than 1.
self.stride_layer = (
keras.layers.AveragePooling2D(
pool_size=self.stride, strides=self.stride, padding="same"
)
if self.stride > 1
else tf.identity
)
# Define the kernel generation layer.
self.kernel_gen = keras.Sequential(
[
keras.layers.Conv2D(
filters=self.channel // self.reduction_ratio, kernel_size=1
),
keras.layers.BatchNormalization(),
keras.layers.ReLU(),
keras.layers.Conv2D(
filters=self.kernel_size * self.kernel_size * self.group_number,
kernel_size=1,
),
]
)
# Define reshape layers
self.kernel_reshape = keras.layers.Reshape(
target_shape=(
height,
width,
self.kernel_size * self.kernel_size,
1,
self.group_number,
)
)
self.input_patches_reshape = keras.layers.Reshape(
target_shape=(
height,
width,
self.kernel_size * self.kernel_size,
num_channels // self.group_number,
self.group_number,
)
)
self.output_reshape = keras.layers.Reshape(
target_shape=(height, width, num_channels)
)
def call(self, x):
# Generate the kernel with respect to the input tensor.
# B, H, W, K*K*G
kernel_input = self.stride_layer(x)
kernel = self.kernel_gen(kernel_input)
# reshape the kerenl
# B, H, W, K*K, 1, G
kernel = self.kernel_reshape(kernel)
# Extract input patches.
# B, H, W, K*K*C
input_patches = tf.image.extract_patches(
images=x,
sizes=[1, self.kernel_size, self.kernel_size, 1],
strides=[1, self.stride, self.stride, 1],
rates=[1, 1, 1, 1],
padding="SAME",
)
# Reshape the input patches to align with later operations.
# B, H, W, K*K, C//G, G
input_patches = self.input_patches_reshape(input_patches)
# Compute the multiply-add operation of kernels and patches.
# B, H, W, K*K, C//G, G
output = tf.multiply(kernel, input_patches)
# B, H, W, C//G, G
output = tf.reduce_sum(output, axis=3)
# Reshape the output kernel.
# B, H, W, C
output = self.output_reshape(output)
# Return the output tensor and the kernel.
return output, kernel测试逆卷积层
# Define the input tensor.
input_tensor = tf.random.normal((32, 256, 256, 3))
# Compute involution with stride 1.
output_tensor, _ = Involution(
channel=3, group_number=1, kernel_size=5, stride=1, reduction_ratio=1, name="inv_1"
)(input_tensor)
print(f"with stride 1 ouput shape: {output_tensor.shape}")
# Compute involution with stride 2.
output_tensor, _ = Involution(
channel=3, group_number=1, kernel_size=5, stride=2, reduction_ratio=1, name="inv_2"
)(input_tensor)
print(f"with stride 2 ouput shape: {output_tensor.shape}")
# Compute involution with stride 1, channel 16 and reduction ratio 2.
output_tensor, _ = Involution(
channel=16, group_number=1, kernel_size=5, stride=1, reduction_ratio=2, name="inv_3"
)(input_tensor)
print(
"with channel 16 and reduction ratio 2 ouput shape: {}".format(output_tensor.shape)
)演绎展示:
with stride 1 ouput shape: (32, 256, 256, 3)
with stride 2 ouput shape: (32, 128, 128, 3)
with channel 16 and reduction ratio 2 ouput shape: (32, 256, 256, 3)图像分类
在本文中,我们将建立一个图像分类器模型。将有两个模型,一个是卷积模型,另一个是渐开线模型。
图像分类模型的灵感主要来自谷歌的卷积神经网络(CNN)教程。
获取 CIFAR10 数据集
# Load the CIFAR10 dataset.
print("loading the CIFAR10 dataset...")
(
(train_images, train_labels),
(
test_images,
test_labels,
),
) = keras.datasets.cifar10.load_data()
# Normalize pixel values to be between 0 and 1.
(train_images, test_images) = (train_images / 255.0, test_images / 255.0)
# Shuffle and batch the dataset.
train_ds = (
tf.data.Dataset.from_tensor_slices((train_images, train_labels))
.shuffle(256)
.batch(256)
)
test_ds = tf.data.Dataset.from_tensor_slices((test_images, test_labels)).batch(256)加载 CIFAR10 数据集...数据可视化
class_names = [
"airplane",
"automobile",
"bird",
"cat",
"deer",
"dog",
"frog",
"horse",
"ship",
"truck",
]
plt.figure(figsize=(10, 10))
for i in range(25):
plt.subplot(5, 5, i + 1)
plt.xticks([])
plt.yticks([])
plt.grid(False)
plt.imshow(train_images[i])
plt.xlabel(class_names[train_labels[i][0]])
plt.show()演绎展示:

卷积神经网络
# Build the conv model.
print("building the convolution model...")
conv_model = keras.Sequential(
[
keras.layers.Conv2D(32, (3, 3), input_shape=(32, 32, 3), padding="same"),
keras.layers.ReLU(name="relu1"),
keras.layers.MaxPooling2D((2, 2)),
keras.layers.Conv2D(64, (3, 3), padding="same"),
keras.layers.ReLU(name="relu2"),
keras.layers.MaxPooling2D((2, 2)),
keras.layers.Conv2D(64, (3, 3), padding="same"),
keras.layers.ReLU(name="relu3"),
keras.layers.Flatten(),
keras.layers.Dense(64, activation="relu"),
keras.layers.Dense(10),
]
)
# Compile the mode with the necessary loss function and optimizer.
print("compiling the convolution model...")
conv_model.compile(
optimizer="adam",
loss=keras.losses.SparseCategoricalCrossentropy(from_logits=True),
metrics=["accuracy"],
)
# Train the model.
print("conv model training...")
conv_hist = conv_model.fit(train_ds, epochs=20, validation_data=test_ds)演绎展示:
building the convolution model...
compiling the convolution model...
conv model training...
Epoch 1/20
196/196 ━━━━━━━━━━━━━━━━━━━━ 6s 15ms/step - accuracy: 0.3068 - loss: 1.9000 - val_accuracy: 0.4861 - val_loss: 1.4593
Epoch 2/20
196/196 ━━━━━━━━━━━━━━━━━━━━ 1s 4ms/step - accuracy: 0.5153 - loss: 1.3603 - val_accuracy: 0.5741 - val_loss: 1.1913
Epoch 3/20
196/196 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.5949 - loss: 1.1517 - val_accuracy: 0.6095 - val_loss: 1.0965
Epoch 4/20
196/196 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.6414 - loss: 1.0330 - val_accuracy: 0.6260 - val_loss: 1.0635
Epoch 5/20
196/196 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.6690 - loss: 0.9485 - val_accuracy: 0.6622 - val_loss: 0.9833
Epoch 6/20
196/196 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.6951 - loss: 0.8764 - val_accuracy: 0.6783 - val_loss: 0.9413
Epoch 7/20
196/196 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.7122 - loss: 0.8167 - val_accuracy: 0.6856 - val_loss: 0.9134
Epoch 8/20
196/196 ━━━━━━━━━━━━━━━━━━━━ 1s 4ms/step - accuracy: 0.7299 - loss: 0.7709 - val_accuracy: 0.7001 - val_loss: 0.8792
Epoch 9/20
196/196 ━━━━━━━━━━━━━━━━━━━━ 1s 4ms/step - accuracy: 0.7467 - loss: 0.7288 - val_accuracy: 0.6992 - val_loss: 0.8821
Epoch 10/20
196/196 ━━━━━━━━━━━━━━━━━━━━ 1s 4ms/step - accuracy: 0.7591 - loss: 0.6982 - val_accuracy: 0.7235 - val_loss: 0.8237
Epoch 11/20
196/196 ━━━━━━━━━━━━━━━━━━━━ 1s 4ms/step - accuracy: 0.7725 - loss: 0.6550 - val_accuracy: 0.7115 - val_loss: 0.8521
Epoch 12/20
196/196 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.7808 - loss: 0.6302 - val_accuracy: 0.7051 - val_loss: 0.8823
Epoch 13/20
196/196 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.7860 - loss: 0.6101 - val_accuracy: 0.7122 - val_loss: 0.8635
Epoch 14/20
196/196 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.7998 - loss: 0.5786 - val_accuracy: 0.7214 - val_loss: 0.8348
Epoch 15/20
196/196 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.8117 - loss: 0.5473 - val_accuracy: 0.7139 - val_loss: 0.8835
Epoch 16/20
196/196 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.8168 - loss: 0.5267 - val_accuracy: 0.7155 - val_loss: 0.8840
Epoch 17/20
196/196 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.8266 - loss: 0.5022 - val_accuracy: 0.7239 - val_loss: 0.8576
Epoch 18/20
196/196 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.8374 - loss: 0.4750 - val_accuracy: 0.7262 - val_loss: 0.8756
Epoch 19/20
196/196 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.8452 - loss: 0.4505 - val_accuracy: 0.7235 - val_loss: 0.9049
Epoch 20/20
196/196 ━━━━━━━━━━━━━━━━━━━━ 1s 4ms/step - accuracy: 0.8531 - loss: 0.4283 - val_accuracy: 0.7304 - val_loss: 0.8962逆向传播神经网络
# Build the involution model.
print("building the involution model...")
inputs = keras.Input(shape=(32, 32, 3))
x, _ = Involution(
channel=3, group_number=1, kernel_size=3, stride=1, reduction_ratio=2, name="inv_1"
)(inputs)
x = keras.layers.ReLU()(x)
x = keras.layers.MaxPooling2D((2, 2))(x)
x, _ = Involution(
channel=3, group_number=1, kernel_size=3, stride=1, reduction_ratio=2, name="inv_2"
)(x)
x = keras.layers.ReLU()(x)
x = keras.layers.MaxPooling2D((2, 2))(x)
x, _ = Involution(
channel=3, group_number=1, kernel_size=3, stride=1, reduction_ratio=2, name="inv_3"
)(x)
x = keras.layers.ReLU()(x)
x = keras.layers.Flatten()(x)
x = keras.layers.Dense(64, activation="relu")(x)
outputs = keras.layers.Dense(10)(x)
inv_model = keras.Model(inputs=[inputs], outputs=[outputs], name="inv_model")
# Compile the mode with the necessary loss function and optimizer.
print("compiling the involution model...")
inv_model.compile(
optimizer="adam",
loss=keras.losses.SparseCategoricalCrossentropy(from_logits=True),
metrics=["accuracy"],
)
# train the model
print("inv model training...")
inv_hist = inv_model.fit(train_ds, epochs=20, validation_data=test_ds)building the involution model...
compiling the involution model...
inv model training...
Epoch 1/20
196/196 ━━━━━━━━━━━━━━━━━━━━ 9s 25ms/step - accuracy: 0.1369 - loss: 2.2728 - val_accuracy: 0.2716 - val_loss: 2.1041
Epoch 2/20
196/196 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.2922 - loss: 1.9489 - val_accuracy: 0.3478 - val_loss: 1.8275
Epoch 3/20
196/196 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.3477 - loss: 1.8098 - val_accuracy: 0.3782 - val_loss: 1.7435
Epoch 4/20
196/196 ━━━━━━━━━━━━━━━━━━━━ 1s 6ms/step - accuracy: 0.3741 - loss: 1.7420 - val_accuracy: 0.3901 - val_loss: 1.6943
Epoch 5/20
196/196 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.3931 - loss: 1.6942 - val_accuracy: 0.4007 - val_loss: 1.6639
Epoch 6/20
196/196 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.4057 - loss: 1.6622 - val_accuracy: 0.4108 - val_loss: 1.6494
Epoch 7/20
196/196 ━━━━━━━━━━━━━━━━━━━━ 1s 6ms/step - accuracy: 0.4134 - loss: 1.6374 - val_accuracy: 0.4202 - val_loss: 1.6363
Epoch 8/20
196/196 ━━━━━━━━━━━━━━━━━━━━ 1s 6ms/step - accuracy: 0.4200 - loss: 1.6166 - val_accuracy: 0.4312 - val_loss: 1.6062
Epoch 9/20
196/196 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.4286 - loss: 1.5949 - val_accuracy: 0.4316 - val_loss: 1.6018
Epoch 10/20
196/196 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.4346 - loss: 1.5794 - val_accuracy: 0.4346 - val_loss: 1.5963
Epoch 11/20
196/196 ━━━━━━━━━━━━━━━━━━━━ 1s 6ms/step - accuracy: 0.4395 - loss: 1.5641 - val_accuracy: 0.4388 - val_loss: 1.5831
Epoch 12/20
196/196 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.4445 - loss: 1.5502 - val_accuracy: 0.4443 - val_loss: 1.5826
Epoch 13/20
196/196 ━━━━━━━━━━━━━━━━━━━━ 1s 6ms/step - accuracy: 0.4493 - loss: 1.5391 - val_accuracy: 0.4497 - val_loss: 1.5574
Epoch 14/20
196/196 ━━━━━━━━━━━━━━━━━━━━ 1s 6ms/step - accuracy: 0.4528 - loss: 1.5255 - val_accuracy: 0.4547 - val_loss: 1.5433
Epoch 15/20
196/196 ━━━━━━━━━━━━━━━━━━━━ 1s 4ms/step - accuracy: 0.4575 - loss: 1.5148 - val_accuracy: 0.4548 - val_loss: 1.5438
Epoch 16/20
196/196 ━━━━━━━━━━━━━━━━━━━━ 1s 6ms/step - accuracy: 0.4599 - loss: 1.5072 - val_accuracy: 0.4581 - val_loss: 1.5323
Epoch 17/20
196/196 ━━━━━━━━━━━━━━━━━━━━ 1s 6ms/step - accuracy: 0.4664 - loss: 1.4957 - val_accuracy: 0.4598 - val_loss: 1.5321
Epoch 18/20
196/196 ━━━━━━━━━━━━━━━━━━━━ 1s 6ms/step - accuracy: 0.4701 - loss: 1.4863 - val_accuracy: 0.4575 - val_loss: 1.5302
Epoch 19/20
196/196 ━━━━━━━━━━━━━━━━━━━━ 1s 6ms/step - accuracy: 0.4737 - loss: 1.4790 - val_accuracy: 0.4676 - val_loss: 1.5233
Epoch 20/20
196/196 ━━━━━━━━━━━━━━━━━━━━ 1s 6ms/step - accuracy: 0.4771 - loss: 1.4740 - val_accuracy: 0.4719 - val_loss: 1.5096比较
在本文中,我们将研究这两种模式,并比较一些要点。
参数
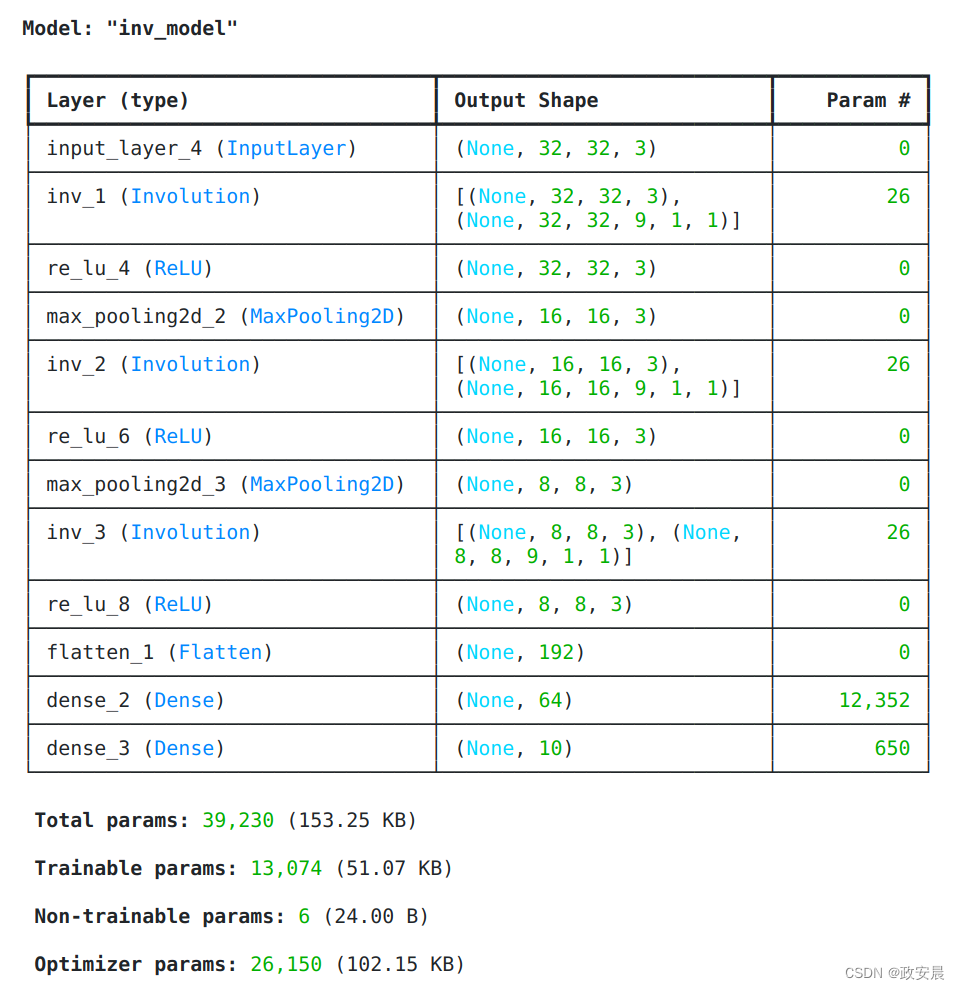
我们可以看到,在类似的架构下,CNN 的参数要比 INN(卷积神经网络)的参数大得多。
conv_model.summary()
inv_model.summary()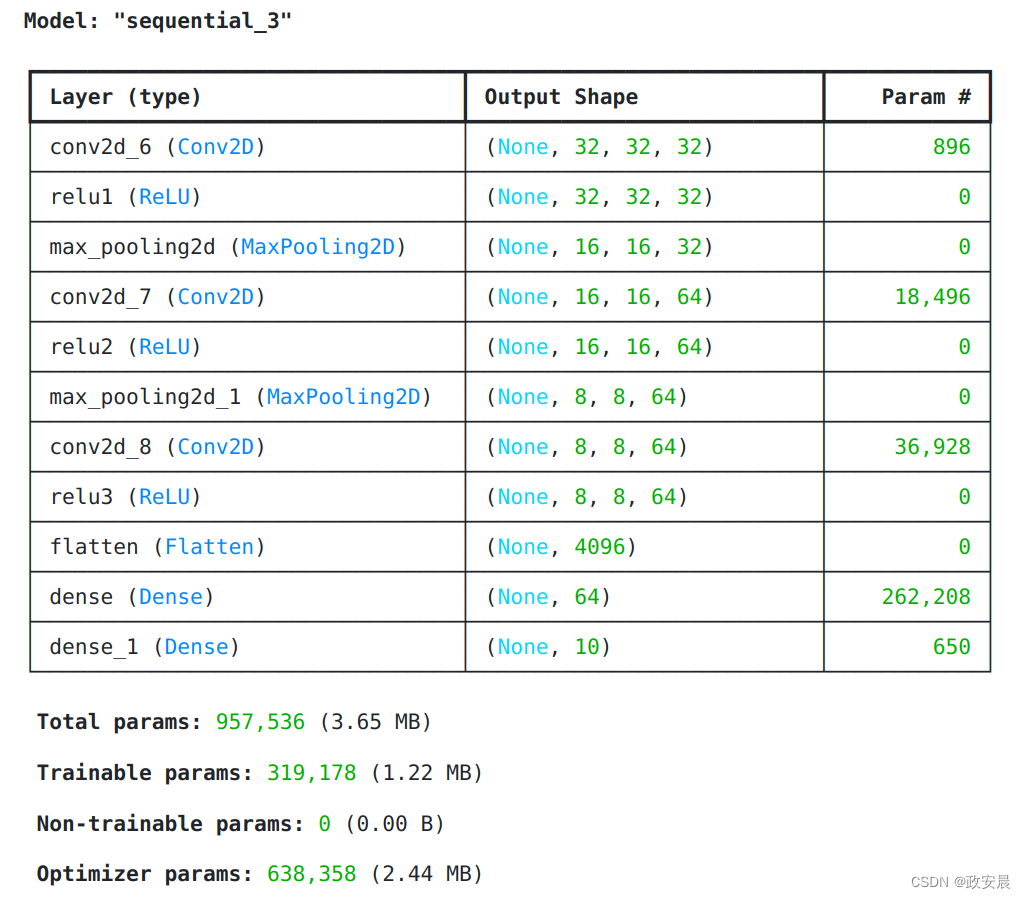
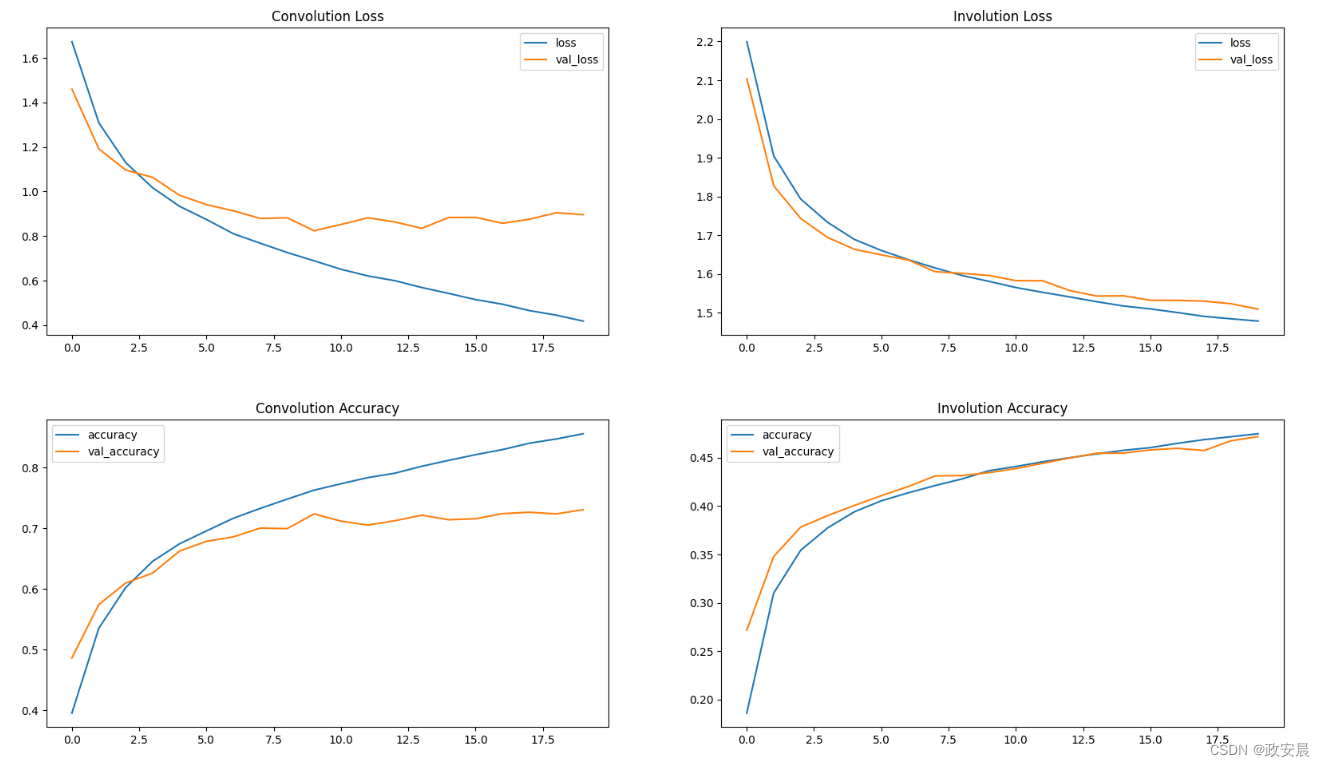
损失图和准确率图
这里的损失图和准确率图表明,INNs 是一种学习速度较慢的学习器(参数较低)。
plt.figure(figsize=(20, 5))
plt.subplot(1, 2, 1)
plt.title("Convolution Loss")
plt.plot(conv_hist.history["loss"], label="loss")
plt.plot(conv_hist.history["val_loss"], label="val_loss")
plt.legend()
plt.subplot(1, 2, 2)
plt.title("Involution Loss")
plt.plot(inv_hist.history["loss"], label="loss")
plt.plot(inv_hist.history["val_loss"], label="val_loss")
plt.legend()
plt.show()
plt.figure(figsize=(20, 5))
plt.subplot(1, 2, 1)
plt.title("Convolution Accuracy")
plt.plot(conv_hist.history["accuracy"], label="accuracy")
plt.plot(conv_hist.history["val_accuracy"], label="val_accuracy")
plt.legend()
plt.subplot(1, 2, 2)
plt.title("Involution Accuracy")
plt.plot(inv_hist.history["accuracy"], label="accuracy")
plt.plot(inv_hist.history["val_accuracy"], label="val_accuracy")
plt.legend()
plt.show()演绎展示:
可视化卷积核
为了使内核可视化,我们取每个内卷内核的 K×K 值之和。不同空间位置上的所有代表都构成了相应的热图。
有人说,"我们提出的内卷让人联想到自我注意,本质上可以成为自我注意的通用版本"。
通过核的可视化,我们确实可以获得图像的注意力图谱。学习到的内卷化内核为输入张量的各个空间位置提供了注意力。
这种针对特定位置的特性使得内卷成为自我注意模型的通用空间。
layer_names = ["inv_1", "inv_2", "inv_3"]
outputs = [inv_model.get_layer(name).output[1] for name in layer_names]
vis_model = keras.Model(inv_model.input, outputs)
fig, axes = plt.subplots(nrows=10, ncols=4, figsize=(10, 30))
for ax, test_image in zip(axes, test_images[:10]):
(inv1_kernel, inv2_kernel, inv3_kernel) = vis_model.predict(test_image[None, ...])
inv1_kernel = tf.reduce_sum(inv1_kernel, axis=[-1, -2, -3])
inv2_kernel = tf.reduce_sum(inv2_kernel, axis=[-1, -2, -3])
inv3_kernel = tf.reduce_sum(inv3_kernel, axis=[-1, -2, -3])
ax[0].imshow(keras.utils.array_to_img(test_image))
ax[0].set_title("Input Image")
ax[1].imshow(keras.utils.array_to_img(inv1_kernel[0, ..., None]))
ax[1].set_title("Involution Kernel 1")
ax[2].imshow(keras.utils.array_to_img(inv2_kernel[0, ..., None]))
ax[2].set_title("Involution Kernel 2")
ax[3].imshow(keras.utils.array_to_img(inv3_kernel[0, ..., None]))
ax[3].set_title("Involution Kernel 3")1/1 ━━━━━━━━━━━━━━━━━━━━ 1s 503ms/step 1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 11ms/step 1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 11ms/step 1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 9ms/step 1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 11ms/step 1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 9ms/step 1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 9ms/step 1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 9ms/step 1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 10ms/step 1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 9ms/step
演绎展示: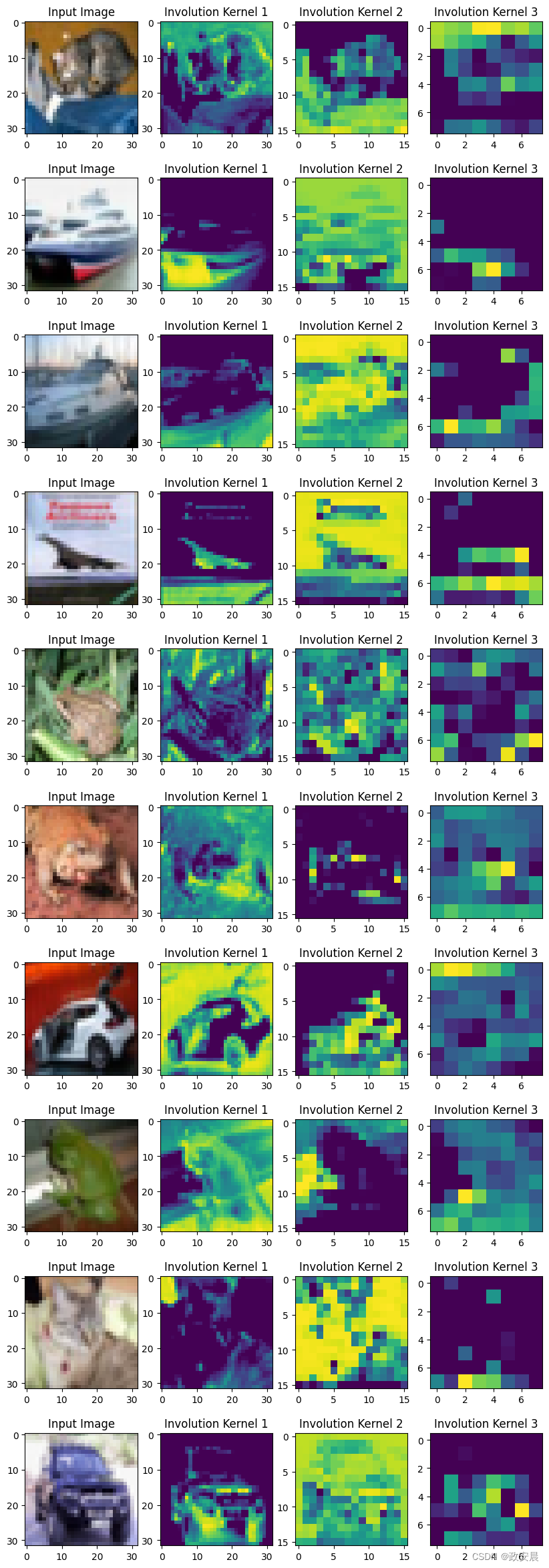
结论
在本示例中,主要重点是构建一个可以轻松重复使用的卷积层。虽然我们的比较是基于一项特定的任务,但您也可以在不同的任务中使用该层,并报告您的结果。
我认为,内卷化的主要启示在于它与自我关注的关系。在很多任务中,特定位置和特定通道处理背后的直觉都是有道理的。







![.[[backup@waifu.club]].svh勒索病毒数据怎么处理|数据解密恢复](https://img-blog.csdnimg.cn/direct/56dbf0e2329a4369b7eb086e4830160e.png)