1 Title
Heterogeneous Hypergraph Embedding for Graph Classification(Xiangguo Sun , PictureHongzhi Yin , PictureBo Liu , PictureHongxu Chen , PictureJiuxin Cao , PictureYingxia Shao , PictureNguyen Quoc Viet Hung)【WSDM 2021】
2 Conclusion
This paper proposes a graph neural network-based representation learning framework for heterogeneous hypergraphs, an extension of conventional graphs, which can well characterize multiple non-pairwise relations. Our framework first projects the heterogeneous hypergraph into a series of snapshots and then we take the Wavelet basis to perform localized hypergraph convolution. Since the Wavelet basis is usually much sparser than the Fourier basis, this study develops an efficient polynomial approximation to the basis to replace the time-consuming Laplacian decomposition. Extensive evaluations have been conducted and the experimental results show the superiority of this method.
3 Good Sentences
1、Most of these methods focus on the pairwise relationships between objects in the constructed graphs.In many real-world scenarios, however, relationships among objects are not dyadic (pairwise) but rather triadic, tetradic, or higher. Squeezing the high-order relations into pairwise ones leads to information loss and impedes expressiveness.(The necessary of hypergraph for model building)
2、But there are key differences between heterogeneous simple graphs and heterogeneous hypergraphs. Even for those homogeneous simple graphs like Figure 2, the same type nodes may also be connected according to different semantics that are represented by different types of hyperedges, making the hypergraph heterogeneous(The challenge of hypergraph meets)
3、However, the above operation has the following two major issues. First, it is not localized in the vertex domain, which cannot fully empower the convolutional operation. Secondly, eigenvectors are explicitly used in convolutions, requiring the eigen-decomposition of the Laplacian matrix for each snapshot in 𝐺.(The disadvantages of the method that used the Fourier transform to learn hypergraph embedding)
在许多现实世界的场景中,对象之间的关系不是二元的(成对的),而是三元的、四元的或更高级的。将高阶关系压缩成成对关系会导致信息损失并妨碍表达能力,为了解决这个问题,引入了超图。
 在线社交论坛上的异构超图示例。有几种类型的超边缘,包括特定用户创建的所有帖子和评论(紫色圆圈)、同一组中的所有帖子和评论(橙色圆圈)以及包含所有评论的帖子(蓝色圆圈)。
在线社交论坛上的异构超图示例。有几种类型的超边缘,包括特定用户创建的所有帖子和评论(紫色圆圈)、同一组中的所有帖子和评论(橙色圆圈)以及包含所有评论的帖子(蓝色圆圈)。
超图挑战1:相同类型的节点也可能根据由不同类型的超边表示的不同语义进行连接,从而使超图异构
超图挑战2:消息可以直接从简单图中的一跳邻居聚合。然而,超图上的消息传播更加复杂。它应该首先在同一个超边内聚合,然后在连接到目标节点的所有超边上聚合。这种差异使得传统的基于GNN的方法不适用于超图
为了解决挑战1,本文首先提取具有不同元路径的简单图快照,然后根据超边类型在这些简单图上构造几个超图快照。分解后,每个快照都是同质的,它们也可以很容易地并行计算,使模型可扩展到大型数据集。
为了解决挑战2,本文通过用小波基代替傅立叶基来设计超图卷积。与顶点域中的方法相比,这种谱方法不需要考虑超图中复杂的消息传递模式,并且还可以执行局部卷积,小波基比傅立叶基稀疏得多,它可以通过多项式有效地近似而无需拉普拉斯分解
一些定义:
Simple Graph Snapshots:.
 根据选择的元路径,可以从原始异构简单图中提取相应的子图。以图a为例,用用户(U)和部门(D)作为节点来表示社交网络,其中边表示友谊(U-U)和从属关系(U-D)。根据元路径U-U和元路径U-D提取路径,然后我们可以生成两个子图作为简单图的两个快照。
根据选择的元路径,可以从原始异构简单图中提取相应的子图。以图a为例,用用户(U)和部门(D)作为节点来表示社交网络,其中边表示友谊(U-U)和从属关系(U-D)。根据元路径U-U和元路径U-D提取路径,然后我们可以生成两个子图作为简单图的两个快照。
Heterogeneous Hypergraph:一个异构超图可以定义为G = {V,,T𝑣,T𝑒,W},其中,V是顶点集,T𝑣是顶点类型集。
是一组超边,T𝑒是超边类型的集合。当|T𝑣|+|T𝑒|>2时,超图是异构的。W是超边权重的对角矩阵,节点和超边之间的关系可以由关联矩阵H 表示

让D𝑣 ∈ 和D𝑒 ∈
分别表示包含顶点度和超边度的对角矩阵,其中
,
。让
,然后拉普拉斯算子就可以表示为
。
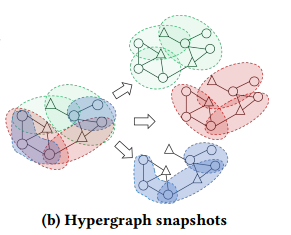
Hypergraph Snapshots:超图G = {V,E}的Snapshot可以被定义为G𝑒 = {V𝑒,E𝑒 }的子图。这里V𝑒和E𝑒分别是V和E的子集,超图快照是根据超边类型生成的,这意味着中的所有超边都应属于同一超边类型。如图所示,三种超图snapshot各包含一种超边类型。
异构超图嵌入:
异构超图嵌入框架的概述如图所示。输入是一个简单的图形。如果简单图是异构的,则先提取具有不同元路径的简单图快照。之后在这些简单图上构造超图,然后将它们分解成多个超图快照,再然后使用开发的超图小波神经网络(HWNN)来学习每个快照中的节点嵌入,然后将这些快照聚合为用于下游分类的综合表示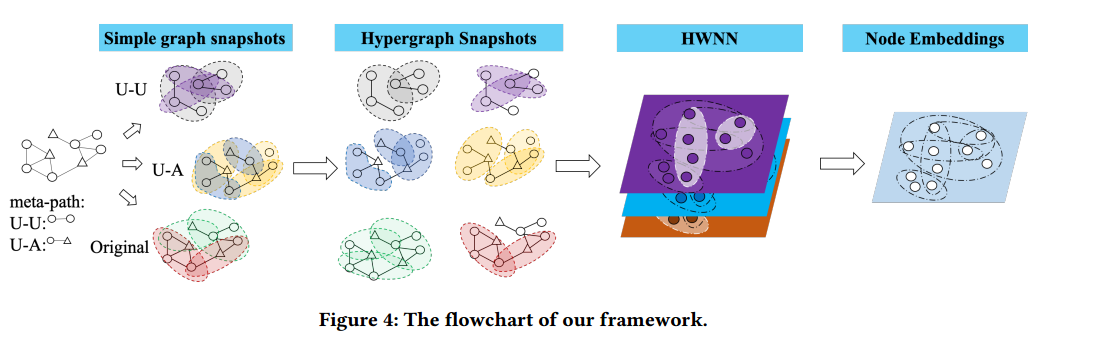
HWNN: Hypergraph Wavelet Neural Networks:
对于每个顶点𝑣𝑖 ∈ V,首先通过全局嵌入矩阵查找其初始向量表示v𝑖 ∈ ,然后将其投影到不同类型超边的子空间中,具有超边类型𝑡𝑒 ∈ T𝑒的超边特定空间中的顶点𝑣𝑖的表示计算如下:
![]() 其中M𝑡𝑒 ∈
其中M𝑡𝑒 ∈是𝑡𝑒的超边特定投影矩阵。
Hypergraph convolution via Fourier basis:
对于从原始异构超图中提取的每个快照G𝑒 = {V𝑒,E𝑒,W},其拉普拉斯矩阵:,其中,
![]() 。
。
令,其中𝑡是
中元素的索引,𝑡 = 1,.......,𝐶,则
![]() ,超图拉普拉斯
,超图拉普拉斯是一个|V | × |V |正半定矩阵,它可以对角化为:
![]() ,其中U是傅立叶基,它包含由其非负特征值排序的标准正交特征向量的完整集合
,其中U是傅立叶基,它包含由其非负特征值排序的标准正交特征向量的完整集合![]() ,根据卷积定理,
,根据卷积定理,和滤波器y的卷积运算
可以写成它们的傅里叶变换的逐元Hadamard之后的傅里叶反变换:

其中![]() 是滤波器的傅里叶变换,
是滤波器的傅里叶变换,![]()
但是,上述操作存在以下两大问题。
首先,它没有定位在顶点域,这不能充分授权卷积操作。其次,特征向量显式地用于卷积,需要对𝐺中的每个快照的拉普拉斯矩阵进行特征分解。为了解决这些问题,本文建议用小波基代替傅立叶基。
选择小波基代替原来的傅立叶基的基本原理如下。首先,小波基比傅里叶基稀疏得多,最适合现代GPU架构进行高效训练。此外,利用小波基的性质,可以更容易地实现有效的多项式近似。
基于这一特征,可以进一步提出图小波的多项式近似,从而不再需要拉普拉斯矩阵的特征分解。最后但并非最不重要的是,小波表示信息扩散过程,非常适合在顶点域实现局部卷积。.
Hypergraph convolution based on wavelets:
![]() 为带有缩放参数s的小波基,
为带有缩放参数s的小波基,
其中![]() ,
,![]() 是超图拉普拉斯算子
是超图拉普拉斯算子的特征值,接着用小波基替换傅里叶基,可得:

在上式中,![]() 是滤波器的谱变换,
是滤波器的谱变换,![]()
![]() 。
。
另外,本文采用StoneWeierstrass定理[10]来逼近图小波,而不需要拉普拉斯矩阵的特征分解,使该方法更加高效。
Stone-Weierstrass定理与多项式近似:
Stone-Weierstrass定理指出热核矩阵![]() restricted to
restricted to![]() ,可以近似为
,可以近似为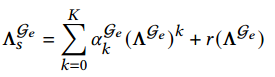 ,其中其中𝐾是多项式阶。
,其中其中𝐾是多项式阶。![]() 包含超图拉普拉斯
包含超图拉普拉斯![]() 的特征值
的特征值
![]() 是每个项都有上界的残差:
是每个项都有上界的残差: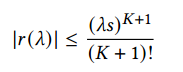
综上,图小波基就可以近似为: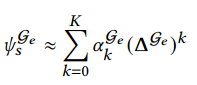 ,而
,而可以看作是
的一阶多项式,该式就可以改写为
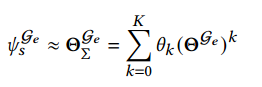 。
。
再之后,可以用s替换-s,使用一组平行的参数来近似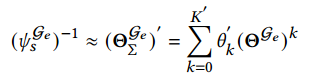 ,
,
于是,有公式![]()
那么,超边卷积神经网络可以表示为: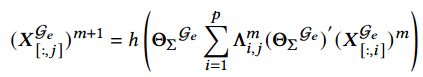 .
.
可以通过将特征变换从卷积中分离出来进一步减少滤波器的数量![]() ,其中,W为特征项目矩阵,设
,其中,W为特征项目矩阵,设式最后一层
的输出,那么对于所有
![]() 的快照,其graph representations为:
的快照,其graph representations为:![]() ,⊕为级联操作,Z为
,⊕为级联操作,Z为,
的级联操作,最后,异构超图G的表示可以通过对其所有快照求和来计算:
![]()
其中𝑓是多层感知器。
在节点分类任务中,待分类类别为。损失函数可以与所有标记样本上的交叉熵误差和投影矩阵上的正则化器相结合
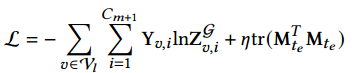 ,其中
,其中是标记节点的集合,
是节点𝑣在类别上的标签值i。如果节点𝑣属于类别i,
![]() 否则为0。𝜂是正则化器的权衡参数。
否则为0。𝜂是正则化器的权衡参数。![]() 被作为正则项,也可以用L-2范式替代。
被作为正则项,也可以用L-2范式替代。
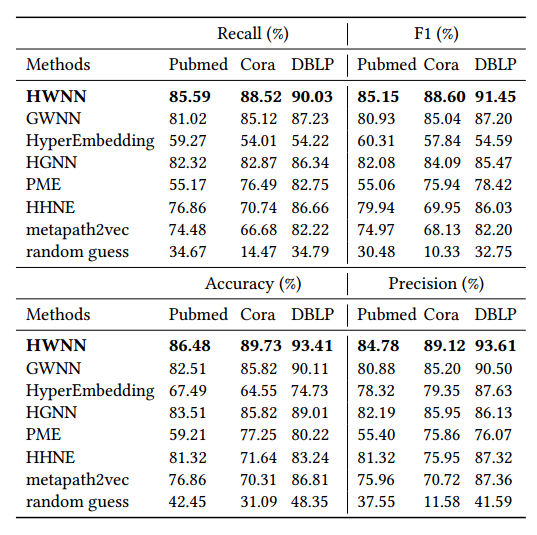
以上是用在节点分类任务上的结果,