文章目录
- 啥也别说了直接进入正题:
- 不连续子序列问题
- 300. 最长递增子序列
- 1143. 最长公共子序列
- 1035. 不相交的线
- 连续子序列问题
- 674. 最长连续递增序列
- 718. 最长重复子数组
- 53. 最大子数组和
- 编辑距离问题
- 392. 判断子序列
- 困难题:115. 不同的子序列
- 583. 两个字符串的删除操作
- 72.编辑距离
- 647. 回文子串
- 516. 最长回文子序列
- 在这里插入图片描述

双非刷leetcode备战2023年蓝桥杯,qwq加油吧,无论结果如何总会有收获!一起加油,我是跟着英雄哥的那个思维导图刷leetcode的,大家也可以看看所有涉及到的题目用leetcode搜索就可以哦,因为避让添加外链,一起加油!!!
动态规划将分为五个板块来讲,本篇为子序列问题
啥也别说了直接进入正题:
本小节将分为以下几个板块来开展:
1. 不连续子序列问题
2.连续子序列问题
3.编辑距离问题
4.回文问题
不连续子序列问题
300. 最长递增子序列
思路:这啥啊,咋规划啊,没思路啊,没做过啊,啥玩意啊。那必不可能没有思路;
其实之前应该遇到过连续的子序列问题,但还真没遇到过这种不连续子序列问题。
没思路,没关系,直接五步走。
把前面的那些动态规划题做完了就很容易有思路,这不就是一个动态规划的题吗??
直接五步走
-
- dp[i]表示什么先要确定下来,我就决定dp[i] 表示的时候在i位置时的最大递增子序列的长度
-
- 初始化,i的最大长度最少就是它本身对不,也就是1;所以全初始化为1就ok了
那接下来就要想如何求i位置上的最大递增子序列的长度。
因为dp[i]表示的是在当前位置的递增的最大长度,怎么求?i之前位置的那些数(之后我们称这些数为j位置上的数)只要有比i位置上的数小的是不是就可以把i位置上的数添加到后面。然后i位置上的最大子序列长度+1;就是dp[i]=dp[j]+1.
这时候我们要考虑到一个问题,就是i前面的j中比i位置上的数小的可能不止一个,那我们求最长子序列就是,求这些之中最大的。也就是dp[i]=max(dp[j]+1,dp[i])
-
- 递推公式
if(nums[i]>nums[j]) { dp[i]=max(dp[i],dp[j]+1); }
okok.现在基本上的问题都解决了dp[i]表示的是什么,表示的是当前位置上的最大递增子序列长度。
- 递推公式
那i前面的位置是不是还有可能比i位置上的数大。太有可能了比如1 5 5 6 4在第五个位置上的dp[i]是2{1,4}
而在第四个位置上的的dp[i]是4{1 5 5 6}
怎门板???
直接用一个res来记录一下不就好了
-
- 遍历顺序:遍历各个位置(i),遍历各个位置之前的位置(j)
for(int i=1;i<N;i++) { for(int j=0;j<i;j++) {}}
- 遍历顺序:遍历各个位置(i),遍历各个位置之前的位置(j)
-
- 结果 return res;
上代马:
class Solution {
public:
int lengthOfLIS(vector<int>& nums) {
int N =nums.size();
vector<int> dp(N,1);
if(N<=1)
{
return N;
}
int res=0;
for(int i=1;i<N;i++)
{
for(int j=0;j<i;j++)
{
if(nums[i]>nums[j])
{
dp[i]=max(dp[i],dp[j]+1);
}
if(res<dp[i])
{
res=dp[i];
}
}
}
return res;
}
};
1143. 最长公共子序列
这个题,太经典了。我都不想说思路了。
核心就是把二维数组的横向当做text1上的各个字符。
然后把二维数组的纵向当做text2上的各个字符。
然后比较在这个位置之前的字符是不是相等的。如果是相等的就把上一个位置上也就是 [ i-1 ] [ j-1 ] 位置上的数加一就完事了
如果不相等就从这个点的上面和左面选一个最大的数赋值过去。
举个例子吧,就举那个实例1的例子:算法进行起来就是这样的
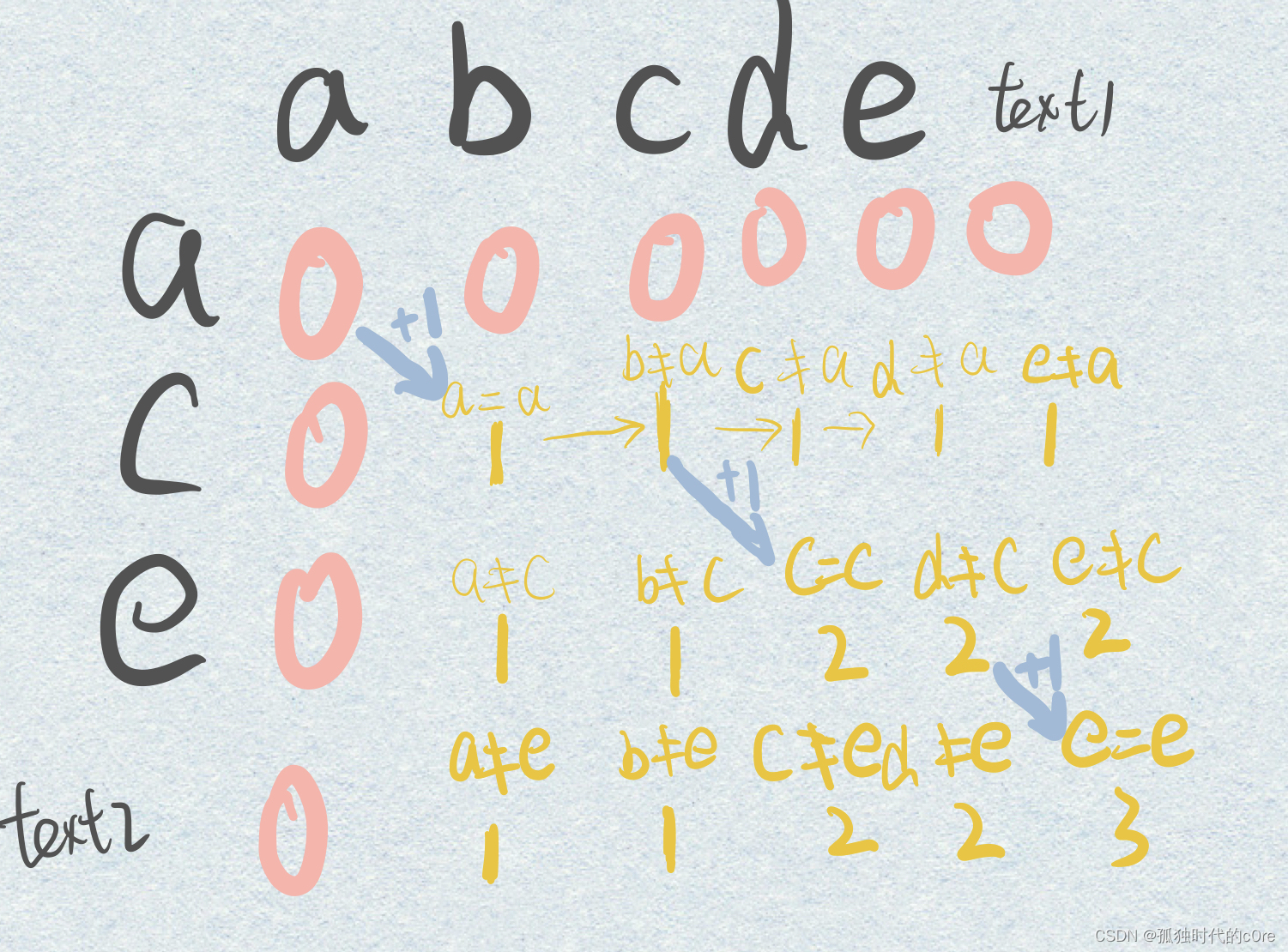
这个的核心就是把这两个串分别表示为数组的纵向和横向来进行动态规划。
上代码:
class Solution {
public:
int longestCommonSubsequence(string text1, string text2) {
int m = text1.length(), n = text2.length();
vector<vector<int>>dp(m+1,vector<int>(n+1));//定义一个二维数组,纵向表示text1,横向表示text2,代表i,j,位置上之前的最长公共子序列
for(int i=1;i<=m;i++)//循环text1
{
for(int j=1;j<=n;j++)//循环text2
{
if(text1[i-1]==text2[j-1])//如果上一个位置上的字符是一样的,就是公共的,所以可以+1
{
dp[i][j]=dp[i-1][j-1]+1;
}
else
{
dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
}
}
}
return dp[m][n];
}
};
1035. 不相交的线
思路:咋能不想交,你想想1 4 2和 1 2 4.的最长公共子序列是多少,是1 4.;这个时候2就处于中间,虽然相等但是他,在中间必然和后面的公共字串相交,所以这个题的本质就是求最大公共子序列
class Solution {
public:
int maxUncrossedLines(vector<int>& nums1, vector<int>& nums2) {
vector<vector<int>>dp(nums1.size()+1,vector<int>(nums2.size()+1));//代表最大连线数量
for(int i=1;i<=nums1.size();i++)
{
for(int j=1;j<=nums2.size();j++)
{
if(nums1[i-1]==nums2[j-1])
{
dp[i][j]=dp[i-1][j-1]+1;
}
else
{
dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
}
}
}
return dp[nums1.size()][nums2.size()];
}
};
连续子序列问题
674. 最长连续递增序列
思路:前一个小于这个,这个的dp就是前一个dp+1;
直接五步走
-
- dp[i]表示在i位置时的最大递增子序列的长度
-
- 初始化,i的最大长度最少就是它本身对不,也就是1;所以全初始化为1就ok了
-
- 递推公式
if(nums[i]>nums[i-1]) { dp[i]=dp[i-1]+1; }用个maxX来记录一下最大值if(maxX<dp[i]) { maxX=dp[i]; }
- 递推公式
-
-
遍历顺序:遍历各个位置(i)` for(int i=1;i<N;i++)
{}`
-
-
- 结果 return maxX;
代码:
- 结果 return maxX;
class Solution {
public:
int findLengthOfLCIS(vector<int>& nums) {
int N=nums.size();
if(N<=1)
{
return N;
}
vector<int> dp(N,1);
int maxX=0;
for(int i=1;i<N;i++)
{
if(nums[i]>nums[i-1])
{
dp[i]=dp[i-1]+1;
}
if(maxX<dp[i])
{
maxX=dp[i];
}
}
return maxX;
}
};
718. 最长重复子数组
记住,子序列默认不连续,子数组默认连续
这个题要和上面那个子序列的题做对比;
这个题就是上题的二维版
直接五步走
-
- dp[i] [j]表示在i,j位置时之前的最大递增子序列的长度
-
- 初始化,相等才能是1,所以全都搞成0;
-
-
递推公式:就是找这个位置的前一位是不是相等白,要是相等,前面就又多了一个就直接加一,用个maxX来记录一下最大值就完事了 ` if(nums1[i-1]==nums2[j-1])
{
dp[i][j]=dp[i-1][j-1]+1;
}if(dp[i][j]>maxX) { maxX=dp[i][j]; }`
-
-
-
遍历顺序:遍历各个位置(i)` for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{}
}`
-
-
- 结果 return maxX;
class Solution {
public:
int findLength(vector<int>& nums1, vector<int>& nums2) {
int n = nums1.size(), m = nums2.size();
vector<vector<int>> dp(n + 1, vector<int>(m + 1, 0));
int maxX=0;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
if(nums1[i-1]==nums2[j-1])
{
dp[i][j]=dp[i-1][j-1]+1;
}
if(dp[i][j]>maxX)
{
maxX=dp[i][j];
}
}
}
return maxX;
}
};
53. 最大子数组和
这个题啊,我做过哈哈哈哈
你想哈,这个玩意有两种情况,一种是如果太小了,都小于0了,我们就可以不要他了,可以重新开始了对不,因为前面的向下都小于0了,那么对于后面的数来说前面这个串就是累赘,累赘还要他干嘛,直接扔掉就好了。
要是相加还大于0的话,那么一切都有希望,要是后面的有个贼大的数就能这个串贼大,所以这个时候不用抛弃,直接搞个maxsum来记录一下结果就完事了。
代码
class Solution {
public:
int maxSubArray(vector<int>& nums) {
int maxsum=INT_MIN;
int sum=0;
for(int i=0;i<nums.size();i++)
{
if(sum>0)
{
sum+=nums[i];
}
else
{
sum=nums[i];
}
if(maxsum<sum)
{
maxsum=sum;
}
}
return maxsum;
}
};
编辑距离问题
392. 判断子序列
不用dp时间复杂度n2的解法应该没有人不会吧,不会把不会吧,你连n2的解法都不会,你行不行啊,**。
暴力n2解法:
class Solution {
public:
bool isSubsequence(string s, string t) {
int k=0,l=0;
while(k<s.size())
{
while(l<t.size())
{
if(s[k]==t[l])
{
k++;
l++;
}
else
{
l++;
}
}
if(l==t.size())
{
break;
}
}
if(k==s.size())
{
return true;
}
else
{
return false;
}
}
};
好了好了,我们讲的是动态规划所以用dp来解一遍;
思路:
直接五步走
-
- dp[i] [j]表示在i,j位置时之前的公共子序列的长度
-
- 初始化,相等才能是1,所以全都搞成0;
-
- 递推公式:就是找这个位置的前一位是不是相等白,要是相等,前面就又多了一个就直接加一不相等就继承下来就完事了
if(s[i-1]==t[j-1]) { dp[i][j]=dp[i-1][j-1]+1; } else { dp[i][j]=dp[i][j-1]; }
- 递推公式:就是找这个位置的前一位是不是相等白,要是相等,前面就又多了一个就直接加一不相等就继承下来就完事了
-
- 遍历顺序:遍历各个位置(i)
for(int i=1;i<=s.size();i++) { for(int j=1;j<=t.size();j++) {}}
- 遍历顺序:遍历各个位置(i)
-
- 结果 要是等于要匹配的串的长度,就存在return true else return false;
class Solution {
public:
bool isSubsequence(string s, string t) {
vector<vector<int>>dp(s.size()+1,vector<int>(t.size()+1,0));
for(int i=1;i<=s.size();i++)
{
for(int j=1;j<=t.size();j++)
{
if(s[i-1]==t[j-1])
{
dp[i][j]=dp[i-1][j-1]+1;
}
else
{
dp[i][j]=dp[i][j-1];
}
}
}
if(dp[s.size()][t.size()]==s.size())
{
return true;
}
else
{
return false;
}
}
};
困难题:115. 不同的子序列
困难题~ 不要怕~
这道题目如果不是子序列,而是要求连续序列的,那就可以考虑用KMP。那不连续怎么办,动态规划啊
科普一下
unsigned int 0~4294967295
int -2147483648~2147483647
unsigned long 0~4294967295
long -2147483648~2147483647
long long的最大值:9223372036854775807
long long的最小值:-9223372036854775808
unsigned long long的最大值:18446744073709551615
__int64的最大值:9223372036854775807
__int64的最小值:-9223372036854775808
unsigned __int64的最大值:18446744073709551615
笑死我了,我定义int 超了。定义long long超了,一看题解只能定义unsigned long long
他那个测试用例中的dp数组相加以后等于9,98 9,690 ,752,1 82,27 7,136。直接把我克制了。
代码:
class Solution {
public:
int numDistinct(string s, string t) {
vector<vector<unsigned long long>> dp(s.size() + 1, vector<unsigned long long>(t.size() + 1));//dp表示s串的前i-1个位置上和t串的前i-1个位置上的子序列的匹配的次数;
for (int i = 0; i < s.size(); i++) dp[i][0] = 1;
//如果t串是空串的话那么s串肯定是包含一个t串的
for (int j = 1; j < t.size(); j++) dp[0][j] = 0;
//如果s串是空串的话那么s串是肯定不包含除0以外的t串的
for (int i = 1; i <= s.size(); i++) {
for (int j = 1; j <= t.size(); j++) {//遍历
//前一位都相同的话。分为两种情况 一种是要前一位一种是不要前一位要这一位,结果就是要前一位和要这一位之和
if (s[i - 1] == t[j - 1]) {
dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];//这个位置上的加上s串前一个位置上的
}
//如果前一位不相同只能要这一位。
else {
dp[i][j] = dp[i - 1][j];//如果不相同就延续s串的上一位继续搞
}
}
}
return dp[s.size()][t.size()];
}
};
583. 两个字符串的删除操作
这叫啥,这叫原题,什么原题,1143求最大公共子序列的原题!!
思路:原题、
代码:
class Solution {
public:
int minDistance(string word1, string word2) {
int len1 = word1.length();
int len2 = word2.length();
vector<vector<int>>dp(len1+1,vector<int>(len2+1));
for(int i=1;i<=len1;i++)
{
for(int j=1;j<=len2;j++)
{
if(word1[i-1]==word2[j-1])
{
dp[i][j]=dp[i-1][j-1]+1;
}
else
{
dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
}
}
}
return len1+len2-(dp[len1][len2]*2);
}
};
72.编辑距离
思路:
这种题肯定是动态规划。
如果一串word1前i-2位是已经经过最短操作完成操作的一个字符串
如果一串word2前j-2位是已经经过最短操作完成操作的一个字符串
操作的最少次数次数记为dp[i-1][j-1]
面对第i-1位和第j-1位 我们应该怎么操作来记录这个位置的操作次数呢?
1:word[i-1]=word[j-1]: 直接继承dp[i-1][j-1]
2: word[i-1]!=word[j-1]: 我们需要通过操作来把他们变成一样的 :这时看似操作有三种添加删除和修改其实添加和删除是一样的比如你让1串删除就相当于让2串添加,最终的效果是一样的,我们可以吧添加的操作看到删除里面去
删除:
1串删除:dp[i][j]=dp[i-1][j]+1(去我们记录的里面找铲除一个后需要的步数再加一个)
2串删除:dp[i][j]=dp[i][j-1]+1
修改:dp[i][j]=dp[i-1][j-1]+1
这样递推公式就推到完了这个题就基本做完了
初始化:
for(int i=0;i<=len1;i++)
{
dp[i][0]=i;//如果word2为0位的话我们的操作就是全删掉
}
for(int j=0;j<=len2;j++)
{
dp[0][j]=j;//如果word2为0位的话我们的操作就是全删掉
}
全部代码:
class Solution {
public:
int minDistance(string word1, string word2) {
int len1=word1.length();
int len2=word2.length();
vector<vector<int>>dp(len1+1,vector<int>(len2+1)); //定义dp数组 为要使word1的前i位变为word2的前j位需要的最小次数;
for(int i=0;i<=len1;i++)
{
dp[i][0]=i;//如果word2为0位的话我们的操作就是全删掉
}
for(int j=0;j<=len2;j++)
{
dp[0][j]=j;//如果word2为0位的话我们的操作就是全删掉
}
for(int i=1;i<=len1;i++)
{
for(int j=1;j<=len2;j++)
{
if(word1[i-1]==word2[j-1])
{
dp[i][j]=dp[i-1][j-1];//如果相等 不必修改 直接继承
}
else
{
dp[i][j]=minx(dp[i-1][j-1],dp[i-1][j],dp[i][j-1])+1;//分别为修改 ,删除word1当前位置,删除word2当前位置所需要的最小次数
}
}
}
return dp[len1][len2];
}
int minx(int a,int b,int c)
{
int minn=min(a,b);
minn = min(minn,c);
return minn;
}
};
647. 回文子串
思路:动态规划
创新点:dp是从i到j位置上是不是一个回文串。注意遍历顺序,和特殊的一些情况,就比较好写
全部代码:
class Solution {
public:
int countSubstrings(string s) {
int len = s.length();
vector<vector<bool>>dp(len+1,vector<bool>(len,false));//dp数组含义是这个s的i到j上的字符串是不是一个回文串
int result = 0;
for(int i=len-1;i>=0;i--)// dp[i+1][j-1]决定了遍历的顺序!一定是一个从下到上从左到右的顺序因为是i+1 j-1位置上的东西要确定是先遍历过的,这点要注意。不能下遍历
{
for(int j=i;j<len;j++)
{
if(j-i==0)//单个字符串
{
dp[i][j]=true;
result++;
}
else if(j-i==1&&s[i]==s[j])//两个字符串
{
dp[i][j]=true;
result++;
}
else if(s[i]==s[j]&&dp[i+1][j-1])//对于其他的字符串判断他的下一位是不是回文就是行了dp[i+1][j-1]是不是回文
{
dp[i][j]=true;
result++;
}
}
}
return result;
}
};
516. 最长回文子序列
思路;这个题和上个题一样啊。dp记录当前串的长度。然后我是用一个res值来记录一下最大值最后返回最大值就行了。回文的题都是这个套路~
class Solution {
public:
int longestPalindromeSubseq(string s) {
int len = s.length();
vector<vector<int>>dp(len+1,vector<int>(len+1));//代表从i到j最长的回文子序列长度
int res = 0;
for(int i=len-1;i>=0;i--)
{
for(int j=i;j<len;j++)
{
if(s[i]==s[j])//要是相等就是回文就+2
{
if(j-i==0)
{
dp[i][j]=1;
if(res<dp[i][j])
{
res=dp[i][j];
}
}
else if(j-i==1)
{
dp[i][j]=2;
if(res<dp[i][j])
{
res=dp[i][j];
}
}
else
{
dp[i][j]=dp[i+1][j-1]+2;
if(res<dp[i][j])
{
res=dp[i][j];
}
}
}
else
{
dp[i][j]=max(dp[i+1][j],dp[i][j-1]);
if(res<dp[i][j])
{
res=dp[i][j];
}
}
}
}
return res;
}
};
Love is worth years.❤
热爱可抵岁月漫长。
本文部分思路来源于网络(做力扣看题解!)如有侵权联系删除~