主要讲和TransE代码的区别，TransE文章的链接

Java版本TransE代码的学习

关于范数的概念

什么是0范数、1范数、2范数？区别又是什么

 初始化向量

初始化关系平面的向量Wr，初始化向量relation_vec,初始化节点向量entity_vec

        Wr_vec = new double[relation_num][vector_dimension];
        for (int i = 0; i < relation_num; i++) {
            for (int j = 0; j < vector_dimension; j++) {
                Wr_vec[i][j] = uniform(-1, 1);
            }
            norm2one(Wr_vec[i]);
        }

        relation_vec = new double[relation_num][vector_dimension];
        for (int i = 0; i < relation_num; i++) {
            for (int j = 0; j < vector_dimension; j++) {
                relation_vec[i][j] = uniform(-1, 1);
            }
        }

        entity_vec = new double[entity_num][vector_dimension];
        for (int i = 0; i < entity_num; i++) {
            for (int j = 0; j < vector_dimension; j++) {
                entity_vec[i][j] = uniform(-1, 1);
            }
        }

负采样方法

对于 1-N 的关系，赋予更高的概率替换头实体，而对于 N-1 的关系，赋予更高的概率替换尾实体。具体地，对每个关系计算其 tph （每个头实体平均对应几个尾实体）和 hpt （每个尾实体平均对应几个头实体）。对于 tph/tph+hpt 越大的，说明是一对多的关系，在负采样时替换头实体，更容易获得 true negative。

tph：每个头实体平均对应几个尾实体

hpt：每个尾实体平均对应几个头实体

left_num.put(i, sum / count); // tph
right_num.put(i, sum / count);

double pr = 1000 * right_num.get(relation_id) / (right_num.get(relation_id) + left_num.get(relation_id));
if (method == 0) {
    pr = 500;
}
if (rand() % 1000 < pr) {//替换头实体}
   else{//替换尾实体}

计算向量的分数

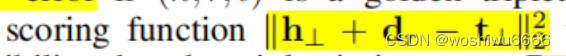
转换

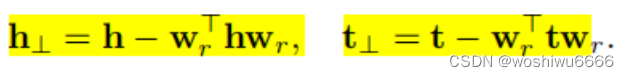
通过转换，得到

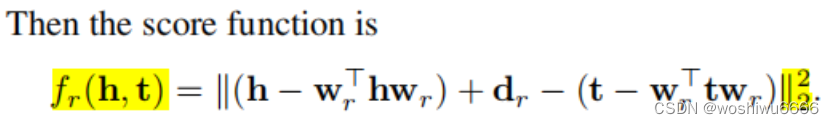
第一个for循环，计算

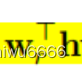和

第二个for循环，计算L2范数的平方，开方以后平方，因为这个向量只有一个值，也就相当于是取绝对值

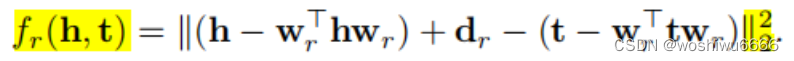
    static double calc_sum(int head, int tail, int relation) {
        double Wrh = 0;
        double Wrt = 0;
        for (int i = 0; i < vector_dimension; i++) {
            Wrh += Wr_vec[relation][i] * entity_vec[head][i];
            Wrt += Wr_vec[relation][i] * entity_vec[tail][i];
        }

        double sum = 0, tmp;
        for (int i = 0; i < vector_dimension; i++) {
            tmp = (entity_vec[tail][i] - Wrt * Wr_vec[relation][i])
                    - relation_vec[relation][i]
                    - (entity_vec[head][i] - Wrh * Wr_vec[relation][i]);
            sum += abs(tmp);
        }
        return sum;
    }

梯度下降

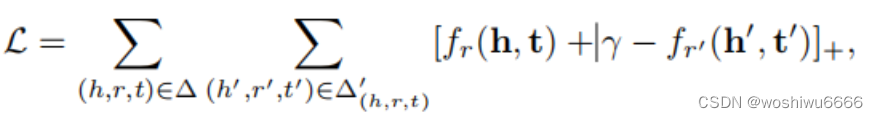
        if (sum1 + margin > sum2) {
            res = margin + sum1 - sum2;
            gradient(head_a, tail_a, relation_a, -1);
            gradient(head_b, tail_b, relation_b, 1);
        }

    private static void gradient(int head, int tail, int relation, double beta) {
        double Wrh = 0;
        double Wrt = 0;
        for (int i = 0; i < vector_dimension; i++) {
            Wrh += Wr_vec[relation][i] * entity_vec[head][i];
            Wrt += Wr_vec[relation][i] * entity_vec[tail][i];
        }

        double sum = 0;
        for (int i = 0; i < vector_dimension; i++) {
            double delta = (entity_vec[tail][i] - Wrt * Wr_vec[relation][i])
                    - relation_vec[relation][i]
                    - (entity_vec[head][i] - Wrh * Wr_vec[relation][i]);
            double x = (delta > 0) ? 1 : -1;
            sum += x * Wr_vec[relation][i];
            relation_vec[relation][i] -= beta * learning_rate * x;
            entity_vec[head][i] -= beta * learning_rate * x;
            entity_vec[tail][i] += beta * learning_rate * x;
            Wr_vec[relation][i] += beta * x * learning_rate  * (Wrh - Wrt);
        }
        for (int i = 0; i < vector_dimension; i++) {
            Wr_vec[relation][i] += beta * learning_rate * sum * (entity_vec[head][i] - entity_vec[tail][i]);
        }
        norm(relation_vec[relation]);
        norm(entity_vec[head]);
        norm(entity_vec[tail]);

        norm2one(Wr_vec[relation]);
        norm(relation_vec[relation], Wr_vec[relation]);
    }

使用L2范数归一化，先求平方和，再开方

norm(relation_vec[relation]);

       static double vec_len(double[] a) {
        // calculate the length of the vector
        double res = 0;
        for (int i = 0; i < vector_dimension; i++) {
            res += sqr(a[i]);
        }
        return sqrt(res);
    }

        static void norm(double[] a) {
        // limit the element a under 1
        double x = vec_len(a);
        if (x > 1) {
            for (int i = 0; i < vector_dimension; i++) {
                a[i] /= x;
            }
        }
    }

dr与Wr的关系限制，dr就是relation，Wr是relation的映射平面

        norm(relation_vec[relation], Wr_vec[relation]);

    static void norm(double[] a, double[] Wr) {
        double sum = 0;
        while (true) {
            for (int i = 0; i < vector_dimension; i++) {
                sum += sqr(Wr[i]);
            }
            sum = sqrt(sum);
            for (int i = 0; i < vector_dimension; i++) {
                Wr[i] /= sum;
            }

            double x = 0;
            for (int i = 0; i < vector_dimension; i++) {
                x += Wr[i] * a[i];
            }
            if (x > 0.1) {
                for (int i = 0; i < vector_dimension; i++) {
                    double tmp = a[i];
                    a[i] -= learning_rate * Wr[i];
                    Wr[i] -= learning_rate * tmp;
                }
            } else {
                break;
            }
        }
        norm2one(Wr);
    }

✖