数学建模----图与网络模型

news2025/1/17 21:32:36

一.图的基本概念与数据结构

1.基本概念

2.图与网络的数据结构

1.邻接矩阵表示法

2.关联矩阵

3.Matlab工具箱简介

1.图的生成

4.问题讨论

1.最短路问题

2.最小生成树问题

一.图的基本概念与数据结构

1.基本概念

点对应于研究对象，根据关系将一些点对应相连，不考虑点的位置与连线的曲直长短，这样形成的一个关系结构就是一个图。记为G=(V,E)，V为顶点集，E是以上述连线为元素的边集。

如果个边都加上方向，则称为有向图，否则称为无向图。如果有的边有方向，有的边无方向，则称为混合图。

点的度：

（1）定义(1)在无向图中，与顶点v关联的边的数目(环算两次)称为v的度，记为d(v)。

（2）在有向图中，从顶点v引出的弧的数目称为v的出度，记为 $d^{+}(v)$

从顶点v引入的弧的数目称为v的入度，记为 $d^{-}(v)$ , $d(v)=d^{+}(v)+d^{-}(v)$ 称为v的度

2.图与网络的数据结构

计算机中描述图与网络有两种方法：邻接矩阵表示法和关联矩阵表示法。

下列讨论中，首先假设 $G=(V,E)$ 是一个简单无向图，顶点集合 $V = \left \{ v_{1},L,v_{n} \right \}$ ,边集 $E=\left \{ e_{1},L,e_{m} \right \}$ ,记 $\left | V \right | =n,\left | E \right | =m$

1.邻接矩阵表示法

邻接矩阵是表示顶点之间相邻关系的矩阵，邻接矩阵记作 $W = (w_{ij})_{n'n}$ ,

当G为赋权图时：

当G为非赋权图时：

2.关联矩阵

对于无向图G，其关联矩阵 $M=(m_{ij})$ 其中，若顶点 $v_{i}$ 与边 $e_{j}$ 关联 $m_{ij}=1$ ;反之 $m_{ij}=0$

3.Matlab工具箱简介

1.图的生成

Graph:无向图
Digraph:有向图
G = graph ----创建空的无向图对象
G = graph(A)----使用邻接矩阵A创建赋权无向图。
G = graph(A,nodes) ----- 试用邻接矩阵A和节点名称nodes创建赋权无向图。
G = graph(s,t)---使用节点对组s，t创建无向图。
G = graph(s,t,weights)---使用节点对组s,t和权重向量weights创建赋权无向图。
G = graph(s,t,weights,nodes)---使用字符向量元胞数组nodes指定节点名称
G = graph(A,[nodes],type) ----- 仅使用邻接矩阵A的上或下三角形阵构造赋权图，type可以是'upper'或'lower'。

2.小tip

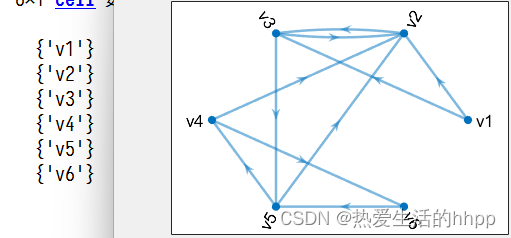
nodes = cellstr(strcat('v',int2str([1:6]')))%%创建节点符号

.

4.问题讨论

1.最短路问题

(1)两个指定顶点之间的最短路径

问题如下，给出了一个连接若干个城镇的铁路网络，在这个网络的两个指定城镇间，找一条最短铁路线。

构造赋权图 $G =(V,E,W)$ ，其中顶点集 $V =\left \{ v_{1},L,v_{n} \right \}$ ，这里 $v_{1},L,v_{n}$ 表示各个小城镇，E为边的集合，邻接矩阵 $W = (w_{ij})_{n'n}$ ，这里 $w_{ij}$ 表示顶点 $v_{i}$ 和 $v_{j}$ 之间直通铁路的距离，若顶点 $v_{i}$ 和 $v_{j}$ 之间无铁路，则 $w_{ij}= ?\propto$ 。问题就是赋权图G中指定的两个顶点 $u_{0},v_{0}$ ，间的具有最小权的路。这条路叫做 $u_{0},v_{0}$ 间的最短路，它的权叫做 $u_{0},v_{0}$ 的距离，亦记作 $d(u_{0},v_{0})$

求解最短路的问题，常用算法为狄克斯特拉(Dijkstra)算法

Dijkstra算法的基本思想是：

采用二维数组邻接矩阵的形式储存图并将图初始化；
选择其中一个顶点作为计算最短路径的起点。
构造一个d一维数组dis[n]，其中n是顶点个数，dis用来记录最短路径距离。初始化dis，其值为图中各点到起点的直接距离（即邻接顶点记为其权值，不相邻的顶点记为∞）；
每次中dis数组中找出最小值，该值就是起点到该点的最短路径距离，（可以将该点加一个标志位已记录该点路径已确定）；
在加入了一个新的确定了点之后就需要更新dis数组，看其余点能否通过这个确定的点到达起始点且距离能够更短。
重复4、5步，直到所有点都找到了最短路径

例（有向图） 已知某人要从出发去旅行，目的地及其交通路线见图4.6所示，线侧数字为所需费用。求该旅行者到目的地的费用最小的旅行路线。

clc, clear, close all
E = [1,2,6; 1,3,3; 1,4,1; 2,5,1; 3,2,2; 3,4,2; 4,6,10; 5,4,6
    5,6,4; 5,7,3; 5,8,6; 6,5,10; 6,7,2; 7,8,4; 9,5,2; 9,8,3];
G = digraph(E(:,1), E(:,2), E(:,3));
[path, d] = shortestpath(G, 1, 8, 'method','positive')
p = plot(G,'EdgeLabel',G.Edges.Weight,'Layout', 'circle');
highlight(p,path,'EdgeColor','r','LineWidth',1.5)

利用MATLAB程序求得 $v_{1}$ 到 $v_{8}$ 的费用最小路径为 $v_{1}\rightarrow v_{3}\rightarrow v_{2}\rightarrow v_{5}\rightarrow v_{8}$ ，对应的最小费用为12。

Dijkstra算法能否求任意两个顶点对之间的最短路？

具体方法——每次以不同的顶点作为起点，用Dijkstra算法求出从该起点到其余顶点的最短路径，反复执行n-1（n为顶点个数）次这样的操作，就可得到每对顶点之间的最短路。

由于这种方法太过麻烦，引入另一算法

（二）所有顶点对之间最短路的---Floyd算法

Floyd算法允许赋权图中包含负权的边或弧，但是，对于赋权图中的每个圈C，要求圈C上所有弧的权总和为非负。

Floyd算法包含三个关键算法：求距离矩阵、求路径矩阵、最短路查找算法。

1.求距离矩阵的算法

1,2,3,,,,,,,,k,k+1,,,,,,,n每增加一个单位相当于多加入一个点

例如A1(中间不经历节点):v0->v1;A2(中间经历过的节点小于等于1):v0->v1 ,v0->v1->v2

2.最小生成树问题

2.1基本概念

连通的五圈图叫做树，记为T；其度为1的顶点称为叶子顶点；显然有边的树至少有两个叶子顶点。

若图G=(V(G),E(G))和树T = (V(T),E(T))满足V(G) = V(T),E(T)属于E(G)，则称T是G的生成树。图G连通的充分必要条件为G有生成树，一个连通的生成树很多。