代码上有注释!!!!!!
本篇主要包括三大部分:
第一部分:导入数据集+导入第三方库+数据集简单介绍与可视化+数据集简单预处理
第二部分:手写神经网络代码实现气温预测(手写)
第三部分:调包搭建神经网络实现气温预测(调包)+找到最优网络模型及其参数
目录
第一部分 准备数据
(一)导入第三方库
(二) 导入数据集
(三)数据可视化
编辑
(四)独热编码处理
(五)数据标准化
第二部分 人工手写神经网络
(一)将数据转换成tensor形式
(二)权重、偏置初始化
(三)设置学习率
(四) 训练网络
第三部分 调包实现神经网络预测气温
(一)设置参数
(二)调用torch.nn中的Sequential序列模块
(三)损失函数
(四)优化器
(五)训练网络
(六)预测结果
(七)预测结果和真实标签进行可视化对比
(八)找到最优模型及其参数
第一部分 准备数据
(一)导入第三方库
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import torch
import torch.optim as optim
import warnings
warnings.filterwarnings("ignore")
%matplotlib inline①import warnings 和 warnings.filterwarnings("ignore"):
导入Python的warnings模块,用于处理警告信息。设置忽略警告信息,这样在后续运行代码时不会显示警告。主要是排除版本不同时的警告。
②%matplotlib inline:
这是Jupyter Notebook的魔术命令,用于在Notebook中显示matplotlib绘制的图形,而不是弹出新窗口显示图形。
(二) 导入数据集
features = pd.read_csv('temps.csv')
#看看数据长什么样子
features.head()前五行数据如下:
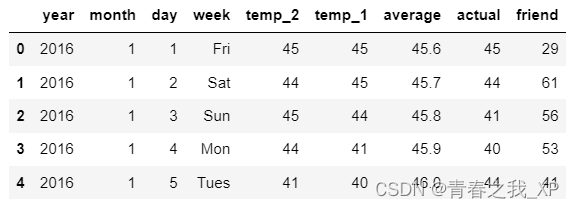
数据表中
- year,moth,day,week分别表示的具体的时间
- temp_2:前天的最高温度值
- temp_1:昨天的最高温度值
- average:在历史中,每年这一天的平均最高温度值
- actual:这就是我们的标签值了,当天的真实最高温度
- friend:这一列是凑热闹的,猜测的可能值,不用管这一列
print('数据维度:', features.shape)![]()
说明数据中一共有348个样本,9个特征。
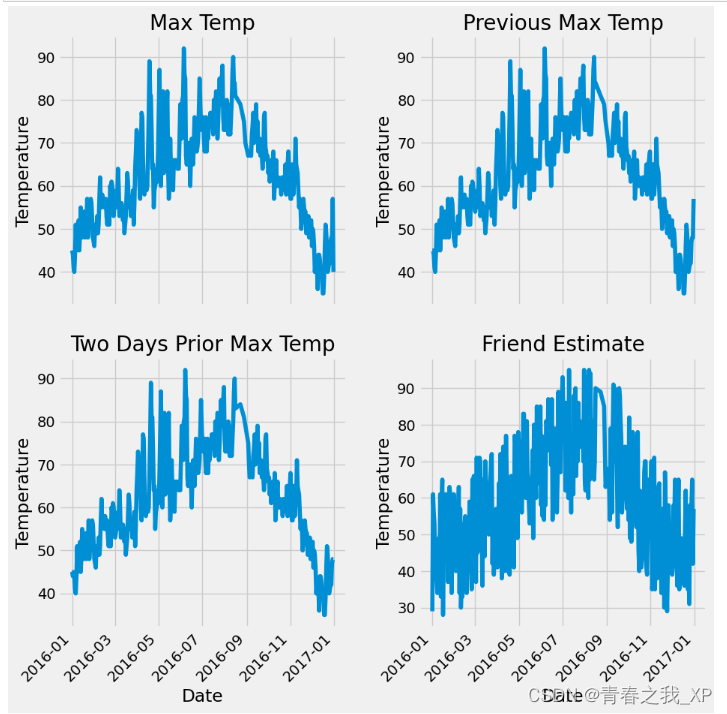
(三)数据可视化
# 处理时间数据
import datetime
# 分别得到年,月,日
years = features['year']
months = features['month']
days = features['day']
# datetime格式
dates = [str(int(year)) + '-' + str(int(month)) + '-' + str(int(day)) for year, month, day in zip(years, months, days)]
dates = [datetime.datetime.strptime(date, '%Y-%m-%d') for date in dates]dates[:5]打印一下dates[:5],查看前五行数据,结果如下:
两个零分别代表小时和分钟

# 准备画图
# 指定默认风格
plt.style.use('fivethirtyeight')
# 设置布局
fig, ((ax1, ax2), (ax3, ax4)) = plt.subplots(nrows=2, ncols=2, figsize = (10,10))
#subplots就是画子图2*2,((ax1, ax2), (ax3, ax4))分别是四个子图
fig.autofmt_xdate(rotation = 45)#x轴标签旋转度
# 标签值
ax1.plot(dates, features['actual'])#表示第一个子图里边x轴和y轴分别是什么
ax1.set_xlabel(''); ax1.set_ylabel('Temperature'); ax1.set_title('Max Temp')
#在这x轴没画值,因为和子图3是一样的y轴,y轴的名称是Temperature,图的名字是Max Temp
# 昨天
ax2.plot(dates, features['temp_1'])
ax2.set_xlabel(''); ax2.set_ylabel('Temperature'); ax2.set_title('Previous Max Temp')
# 前天
ax3.plot(dates, features['temp_2'])
ax3.set_xlabel('Date'); ax3.set_ylabel('Temperature'); ax3.set_title('Two Days Prior Max Temp')
#猜测的数值
ax4.plot(dates, features['friend'])
ax4.set_xlabel('Date'); ax4.set_ylabel('Temperature'); ax4.set_title('Friend Estimate')
plt.tight_layout(pad=2)#每个子图之间的间隔结果如下:
(四)独热编码处理
# 独热编码 one-hot
# features = pd.get_dummies(features)#帮你判断哪一列是字符串,自动地帮你把字符串直接展开
features = pd.get_dummies(features).astype(int)#输出打印体会一下加不加.astype(int)的区别
features.head(5)前五行数据如下:

# 标签
labels = np.array(features['actual'])
# 在特征中去掉标签
features= features.drop('actual', axis = 1)#把标签这一列踢出去
# 名字单独保存一下,以备后患
feature_list = list(features.columns)
# 转换成合适的格式
features = np.array(features)
features.shape 
(五)数据标准化
#标准化
from sklearn import preprocessing
#preprocessing预处理模块
input_features = preprocessing.StandardScaler().fit_transform(features)结果如下:

如上: 现在所有的值都是数组的结构,但torch要tensor的格式结构,所以下面要将数组形式转换成tensor的形式。
第二部分 人工手写神经网络
(一)将数据转换成tensor形式
#把要用的数据转换成tensor的格式
x = torch.tensor(input_features, dtype = float)
y = torch.tensor(labels, dtype = float)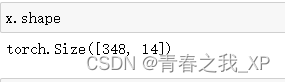
x就作为输入数据,是348*14的维度
(二)权重、偏置初始化
# 权重参数初始化
#w,b都是随机初始化
weights = torch.randn((14, 128), dtype = float, requires_grad = True)
biases = torch.randn(128, dtype = float, requires_grad = True)
weights2 = torch.randn((128, 1), dtype = float, requires_grad = True)
biases2 = torch.randn(1, dtype = float, requires_grad = True) requires_grad = True:进行计算梯度
在这里构建了两个隐藏层,权重w和偏置b都是进行的随机初始化
由于输入数据的维度是384*14
故第一个隐藏层的权重weights是14*128的矩阵,偏置biases长度为128
第二个隐藏层的权重weights2是128*1的行向量,偏置biases2长度为1
因为这里是做回归,也就是预测某一时刻的温度,最终输出的是一个值,故最终的权重weights的维度是128*1

这里补充一点:
输入数据x的维度是348*14,第一个隐藏层的权重weights维度为14*128,那么x*weights做矩阵运算后的结果维度是348*128,但是偏置biases的维度是torch.Size([128]),相当于可以看作是有128个元素的行向量,那么一个348*128的矩阵,怎么和一个1*128的行向量进行加法运算呢?
在这种情况下,PyTorch会自动将大小为 [128] 的张量 biases扩展为大小为 [348, 128] 的张量,使得两个张量的形状相匹配,然后再进行逐元素的加法运算。具体来说,PyTorch会将大小为 [128] 的行向量biases 在第二维上进行复制,扩展为大小为 [348, 128] 的矩阵,然后再与x*weights的结果进行逐元素相加。
(三)设置学习率
learning_rate = 0.001 学习率是可以自己设置的
更新参数的话,我们要沿着一个方向进行参数更新,这个学习率就是告诉我们要沿着这个方向走多大的距离
一般来说,学习率要相对小一点,如果太大了,模型可能做的就相对没有那么好了
(四) 训练网络
losses = []#损失
#迭代更新1000次
for i in range(1000):
# 计算隐层
hidden = x.mm(weights) + biases
#x.mm就是一个矩阵乘法 x*w+b
#一般计算好隐藏层后,都要进行一个非线性映射
#非线性映射里边也有很多函数,比如这里就用到了rule,小于0的时候都等于0,大于0的时候都等于x,y=x
# 加入激活函数
hidden = torch.relu(hidden)#得到实际隐藏层结果
# 预测结果
predictions = hidden.mm(weights2) + biases2
#计算损失
loss = torch.mean((predictions - y) ** 2) #计算的是均方误差
#现在loss是tensor的格式,如果要画图的话,需要的是数组的格式
losses.append(loss.data.numpy())
# 打印损失值
#每隔一百次打印一次损失
if i % 100 == 0:
print('loss:', loss)
#返向传播计算
loss.backward()
#更新参数w,b
#在这里这么理解一下,一会其实可以调包的
weights.data.add_(- learning_rate * weights.grad.data) #weights.grad.data取这一次反向传播的梯度值
#沿着梯度的反方向进行更新,所以有这个-负号
biases.data.add_(- learning_rate * biases.grad.data)
weights2.data.add_(- learning_rate * weights2.grad.data)
biases2.data.add_(- learning_rate * biases2.grad.data)
# 每次迭代都得记得清空
#每一次迭代都应该是独立的,和上一次没关系
#torch如果没有清零,它会累加
weights.grad.data.zero_()
biases.grad.data.zero_()
weights2.grad.data.zero_()
biases2.grad.data.zero_()
通过下边的结果,可以发现它的losse是随着迭代次数的增加不断降低的,最终趋于平稳。
结果如下:
下边是迭代结束后第一个隐藏层权重和偏置的参数,明显和初始随机初始化的参数不同,说明参数进行了梯度更新。
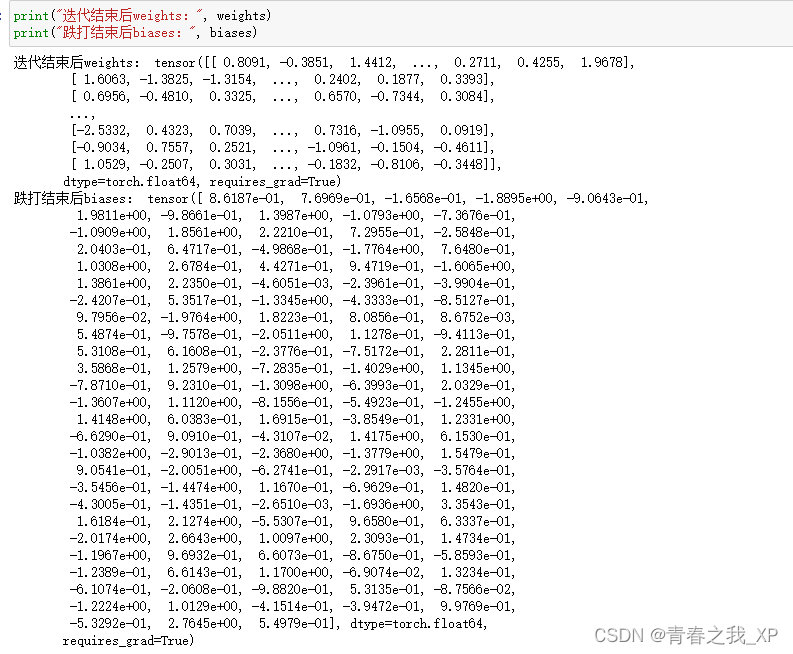
注意:
循环结束后打印的参数值是最后一次迭代后的参数值,但不一定是最优参数值。要获取最优参数值,需要在训练过程中记录并比较每次迭代的性能,从而找到最佳的参数。
第三部分 调包实现神经网络预测气温
(一)设置参数
input_size = input_features.shape[1]#输入特征的个数 14个
hidden_size = 128#隐藏层 可以自己改
output_size = 1#输出值 一个
batch_size = 16input_size表示输入特征的个数,这里是14个
hidden_size = 128:隐藏层有128个隐藏单元。
output_size = 1:这行代码定义了输出值的大小,即模型输出一个标量值。
batch_size:表示每个批次包含16个样本
(二)调用torch.nn中的Sequential序列模块
在调包环节中,和我们第二部分手写神经网络代码不同,权重参数、偏置参数是自动帮我们初始化的
#下边就是调包环节了
#torch.nn中的一个Sequential序列模块,就是按顺序,先执行第一个,再执行第二个,以此类推
#我定义的序列叫做my_nn
my_nn = torch.nn.Sequential(
torch.nn.Linear(input_size, hidden_size),
#全连接层,权重参数是自动帮我们初始化的
torch.nn.Sigmoid(),#nn.ReLu()
#激活函数
torch.nn.Linear(hidden_size, output_size),
)(三)损失函数
cost = torch.nn.MSELoss(reduction='mean')#损失函数 torch.nn.MSELoss:这是 PyTorch 中用于计算均方误差的类。
reduction='mean':这是 torch.nn.MSELoss 类的一个参数,用于指定损失的计算方式。
在这里,设置为 'mean' 表示计算所有样本的均方误差后再取平均值作为最终损失值
(四)优化器
optimizer = torch.optim.Adam(my_nn.parameters(), lr = 0.001)Adam优化器效率高 效果好
my_nn.parameters()表示将神经网络模型my_nn的所有参数传递给优化器,以便优化这些参数。lr=0.001表示学习率为0.001,即Adam优化器在更新参数时所采用的学习率。
(五)训练网络
# 训练网络
losses = []
for i in range(1000):
batch_loss = []
# MINI-Batch方法来进行训练
for start in range(0, len(input_features), batch_size):
end = start + batch_size if start + batch_size < len(input_features) else len(input_features)
# 如果 start + batch_size 的结果小于 input_features 的长度(即 len(input_features)),则将 end 的值设为 start + batch_size。
# 否则,如果 start + batch_size 的结果大于或等于 input_features 的长度,那么 end 的值将设为 len(input_features)
xx = torch.tensor(input_features[start:end], dtype = torch.float, requires_grad = True)
yy = torch.tensor(labels[start:end], dtype = torch.float, requires_grad = True)
prediction = my_nn(xx)
loss = cost(prediction, yy)
optimizer.zero_grad()#梯度清零
loss.backward(retain_graph=True)#反向传播
optimizer.step()#反向传播之后再进行参数更新
batch_loss.append(loss.data.numpy())
#print(len(batch_loss))#结果是22 len(input_features)=348 batch_size=16,21*16+12=348
# 打印损失,每更新迭代一百次打印一次损失
if i % 100==0:
losses.append(np.mean(batch_loss))
# print(losses)
print(i, np.mean(batch_loss))结果如下:

在这段代码中,通过迭代训练神经网络来降低损失函数值,使得神经网络的预测结果更接近真实标签。在每次迭代过程中,会计算一个 mini-batch 的损失值,并根据这个 mini-batch 更新神经网络的参数。
最终目的是通过不断迭代训练,使得损失函数值逐渐减小,达到一个较好的模型效果。
# 在代码中,损失值逐渐减小的原因可能有以下几点:
梯度下降优化算法:通过调用 optimizer.step() 方法,使用梯度下降算法来更新神经网络的参数,使得损失值逐渐减小。
学习率调整:在梯度下降算法中,学习率的设置对模型训练的效果有很大影响。合适的学习率能够使得模型更快地收敛到最优解。
迭代次数:在迭代次数足够多的情况下,模型有更多的机会逐渐优化参数,从而使得损失值逐渐减小。
Mini-batch 训练:使用 mini-batch 训练方法,可以更有效地利用计算资源,同时也有助于模型的收敛。
综合以上因素,随着迭代次数的增加,损失值逐渐减小是一个正常的训练过程。当损失值趋于稳定时,可以认为模型已经收敛到一个较好的状态。
(六)预测结果
x = torch.tensor(input_features, dtype = torch.float)
predict = my_nn(x).data.numpy() #每一个样本,也就是每一天的预测值预测结果如下:
(七)预测结果和真实标签进行可视化对比
# 转换日期格式
dates = [str(int(year)) + '-' + str(int(month)) + '-' + str(int(day)) for year, month, day in zip(years, months, days)]
dates = [datetime.datetime.strptime(date, '%Y-%m-%d') for date in dates]
# 创建一个表格来存日期和其对应的标签数值
true_data = pd.DataFrame(data = {'date': dates, 'actual': labels})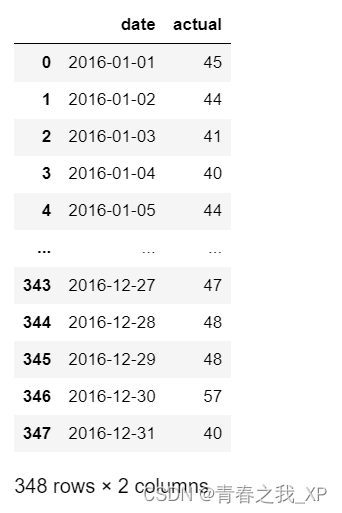
# 同理,再创建一个来存日期和其对应的模型预测值
months = features[:, feature_list.index('month')]
days = features[:, feature_list.index('day')]
years = features[:, feature_list.index('year')]
test_dates = [str(int(year)) + '-' + str(int(month)) + '-' + str(int(day)) for year, month, day in zip(years, months, days)]
test_dates = [datetime.datetime.strptime(date, '%Y-%m-%d') for date in test_dates]
predictions_data = pd.DataFrame(data = {'date': test_dates, 'prediction': predict.reshape(-1)}) 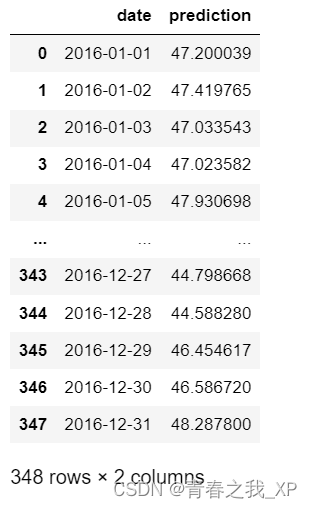
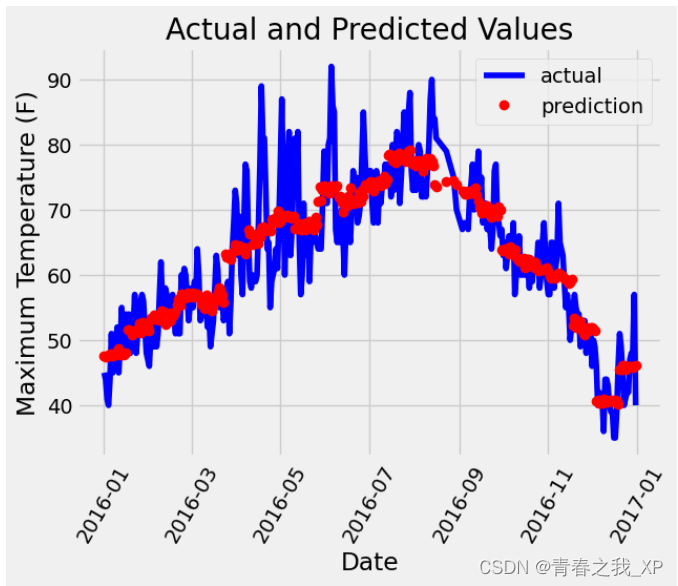
# 真实值
plt.plot(true_data['date'], true_data['actual'], 'b-', label = 'actual')
# 预测值
plt.plot(predictions_data['date'], predictions_data['prediction'], 'ro', label = 'prediction')
plt.xticks(rotation = 60)
plt.legend()#添加图例
# 图名
plt.xlabel('Date'); plt.ylabel('Maximum Temperature (F)'); plt.title('Actual and Predicted Values');
结果如下:
(八)找到最优模型及其参数
我们试想,上边预测出来的结果,是在最优参数模型情况下吗?其实并不是的,是在最后一次迭代结束后的参数基础上进行的预测。
下边我们一起学习一下寻找最优模型及其参数的过程。
# 训练网络
losses = []
# 初始化 best_loss 为一个很大的值,确保第一次比较不会出错
best_loss = float('inf')
import copy
for i in range(1000):
batch_loss = []
# MINI-Batch方法来进行训练
for start in range(0, len(input_features), batch_size):
end = start + batch_size if start + batch_size < len(input_features) else len(input_features)
# 如果 start + batch_size 的结果小于 input_features 的长度(即 len(input_features)),则将 end 的值设为 start + batch_size。
# 否则,如果 start + batch_size 的结果大于或等于 input_features 的长度,那么 end 的值将设为 len(input_features)
xx = torch.tensor(input_features[start:end], dtype = torch.float, requires_grad = True)
yy = torch.tensor(labels[start:end], dtype = torch.float, requires_grad = True)
prediction = my_nn(xx)
#print(prediction)
loss = cost(prediction, yy)
optimizer.zero_grad()#梯度清零
loss.backward(retain_graph=True)#反向传播
optimizer.step()#反向传播之后再进行参数更新
batch_loss.append(loss.data.numpy())
#print(len(batch_loss))#结果是22 len(input_features)=348 batch_size=16,21*16+12=348
# 计算整体损失
xx_val = torch.tensor(input_features, dtype=torch.float)
yy_val = torch.tensor(labels, dtype=torch.float)
prediction_val = my_nn(xx_val)
loss_val = cost(prediction_val, yy_val)
val_loss = loss_val.data.numpy()
# 如果当前epoch的验证损失更低,则保存当前模型的权重
if val_loss < best_loss:
best_loss = val_loss
best_model_weights = copy.deepcopy(my_nn.state_dict())
# # 打印损失
# if i % 100==0:
# losses.append(np.mean(batch_loss))
# # print(losses)
# print(i, np.mean(batch_loss))这里,我们在原先的代码上,做了一点小改动。
best_loss = float('inf'):表示最优损失,初始化 best_loss 为一个很大的值,确保第一次比较不会出错。
要得到最优情况下的模型,需要在训练过程中保存性能最好的模型权重。这可以通过在每次迭代结束时计算损失,并将其与之前的最佳损失进行比较来实现。如果当前迭代的损失更低,则保存当前模型的权重。
best_model_weights = copy.deepcopy(my_nn.state_dict()):执行这行代码,你可以保存当前神经网络模型的参数状态,以便在后续的训练过程中使用或恢复模型的状态。
最优参数如下:

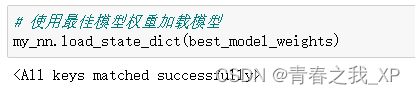
<All keys matched successfully>的运行结果表示成功地将最佳模型的权重加载到了神经网络模型中。这意味着load_state_dict()方法成功地将最佳模型的权重参数与当前神经网络模型的相应参数进行匹配,并将最佳模型的权重参数加载到了当前模型中。
因此,<All keys matched successfully>的输出表明加载权重的过程顺利完成,当前模型已经成功地更新为最佳模型的状态,可以继续使用这个模型进行预测或其他任务。