给你一个n*n矩阵,按照顺序填入1到n*n的数,例如n=5,该矩阵如下
(这是一个题目,但是我这个写法在牛客刷题中是不能正确的得分的,但是我找到了各个关系,然后分享给大家)
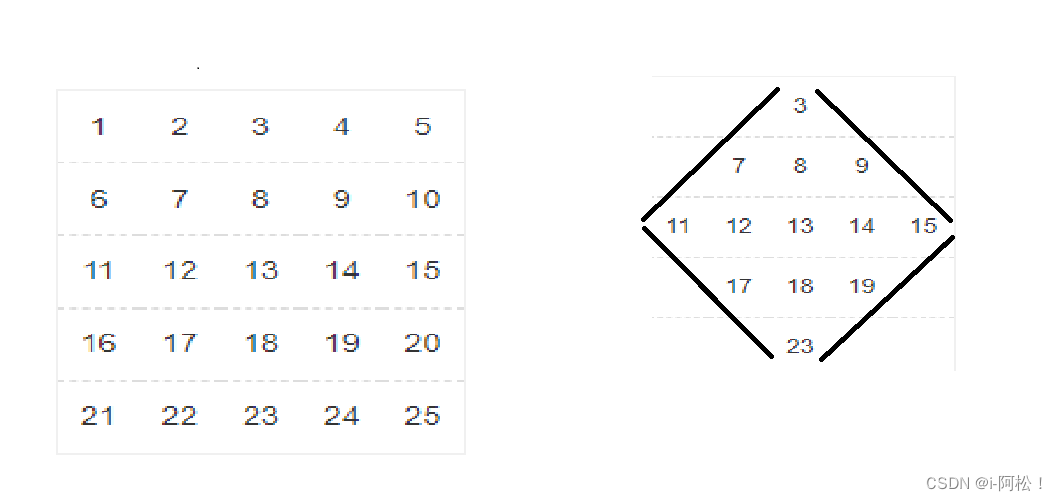
然后再对其进行求和处理,是对右侧图的所有的和进行处理
那么我们解决问题要有以下几步
- 在二维数组中将数字1-----n存到二维数组中
- 找到他们之前的关系,也就是三角形的输入
- 然后在去求和
首先是来进行数据存到数组中,二维数组,行*列=总数 那么就提前定义一个数字,然后在自增,将其存到二维数组中吧那就是这个样子的
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
arr[i][j] = num++;
}
} //前提给num的初始值是1,然后可以执行
那么其实说到底就是第二步是最重要的需要找到四个关系
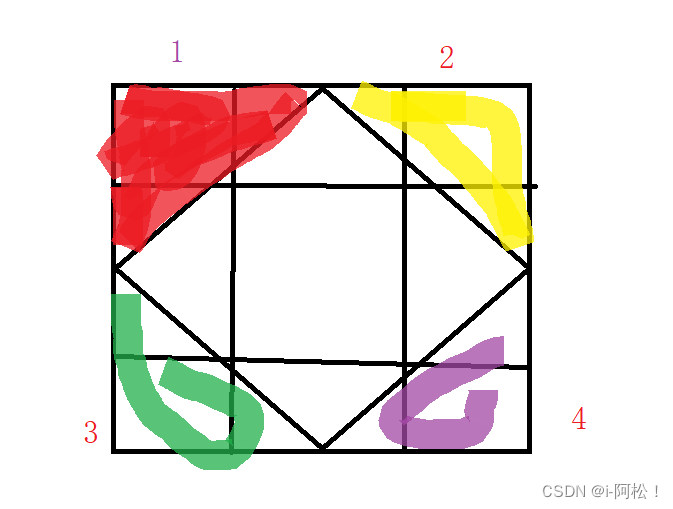
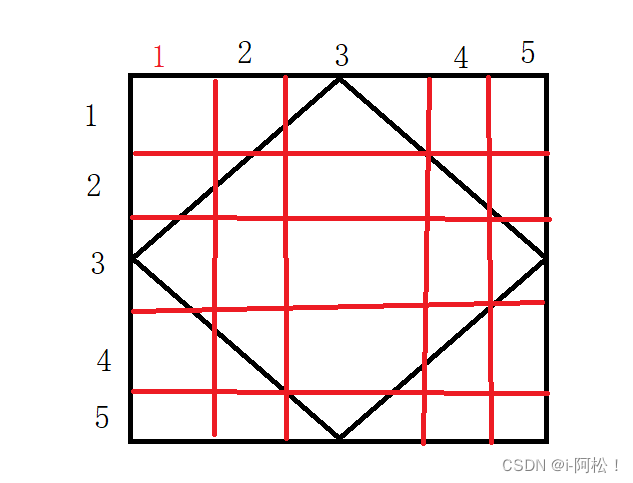
其实应该是5*5的这里(这里数组都是从0开始)
for (int i = 0; i < n / 2; i++) {
for (int j = 0; j < n / 2 - i; j++) {
arr[i][j] = 0;
} //左上角
}
规律是:首先第一个是就在前两行所以小于n/2 也就是2 那么行就是 0 1
看 列了先输出是两个,然后变成了一个,那么想想这样要和谁有关呢,当然是行,所以在你的可变范围内就变成了n/2-i 变化范围是 2-0 =2 2-1=1 所以就是刚好满足 2 1 是不是很妙
for (int i = 0; i < n / 2; i++) { //3 4 列
for (int j = n / 2 + 1 + i; j < n; j++) {
arr[i][j] = 0;
} //右上角
}
第二个部分 :
行还是不变的就是 1 -2 行,但是列缺变成了3-4 这时候还是要找关系的,第一行的时候是先是2
然后第二行的时候是1 然后行是1 然后行是2 那么这个关系就是n / 2 + 1 + i;开始,因为第一行的时候他的数值是 3 4 然后第二行的时候,i为1 了然后就是4 所以只能输出一个
for (int i = n / 2 + 1; i < n; i++) { //3-- 4 行
for (int j = 0; j < i - n / 2; j++) { // 1--2
arr[i][j] = 0; //左下角
}
}
第三部分:
这时候看到了那个行数已经改变了,变成了3 4 ,但是你的列的输出是在1 2,而且需要归零的是i30 和i 40 i41 开始输出的是一个然后输出的是两个这个关系怎么找呢很明显方然是和行有关,毕竟他从三变成了四,而你的输入是三行是1 四行是2 中间差了n/2所有这就是 i - n/2,然后进行输出
for (int i = n / 2 + 1; i < n; i++) { //3-- 4 行
for (int j = n / 2 + (n - i); j < n; j++) { // 1--2
arr[i][j] = 0; //刚开始是1 ---2
}
} //
第四部分也就是最后一个格格的输出
自然和前边一样时从行不变是在 3 4 但是输是在右下侧,输出的顺序是1 2个那么怎么开始呢
其实这个时候你不能去限制上限,只能去改变下限 自然开始是改变上限,也就是你的输入模式
那么怎么做呢,开始的时候是输入第三行是一个数字,第四行是2 个那么和3 4 行有关系吗,当然是有关系的那么关系就是在 2+(5-3) <4 然后是2+(5-4) <4 这个就有俩了所以关系就是--------:n / 2 + (n - i)
说明:我说的行和列是 0---4
输出样例:
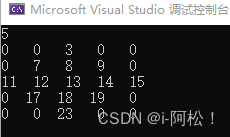
这是那段代码,课自行参考
#include <iostream>
#include<iomanip>
int func(int x);
using namespace std;
int main()
{
int arr[50][50] = { 0 };
int con, n, num = 1, sum = 0, m, s = 0;
cin >> con; //组
while (con > 0) {
cin >> n; //数组
m = func(n);
cout << m<<endl;
con--;
}
return 0;
}
int func(int x)
{
int arr[50][50] = { 0 };
int n, num = 1, sum = 0;
//cin >> n;
n = x;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
arr[i][j] = num++;
}
} //输入了n行n列的数组
for (int i = 0; i < n / 2; i++) {
for (int j = 0; j < n / 2 - i; j++) {
arr[i][j] = 0;
} //左上角
}
for (int i = 0; i < n / 2; i++) { //3 4 列
for (int j = n / 2 + 1 + i; j < n; j++) {
arr[i][j] = 0;
} //右上角
}
for (int i = n / 2 + 1; i < n; i++) { //3-- 4 行
for (int j = 0; j < i - n / 2; j++) { // 1--2
arr[i][j] = 0; //左下角
}
}
for (int i = n / 2 + 1; i < n; i++) { //3-- 4 行
for (int j = n / 2 + (n - i); j < n; j++) { // 1--2
arr[i][j] = 0; //刚开始是1 ---2
}
} // 3
//输出
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
sum += arr[i][j];
}
}
return sum;
}