树状数组+例题

news2024/11/22 10:32:13

一、树状数组的定义

树状数组 或 二元索引树（Binary Indexed Tree），现多用于高效计算数列的前缀和，区间和。它可以以 $l o g (n)$ 的时间得到任意前缀和，也支持在 $l o g (n)$ 时间内支持动态单点值的修改。空间复杂度 $O (n)$ 。

二、树状数组的作用

树状数组最核心的两个操作分别是;

int sum(int idx):以 $l o g (n)$ 的时间返回，从 (1 ~ idx) 的前缀和。
void add(int idx,int k):以 $l o g (n)$ 的时间，进行单点修改。

其他的一些操作都是在这两个函数基础上的拓展。

三、树状数组的结构

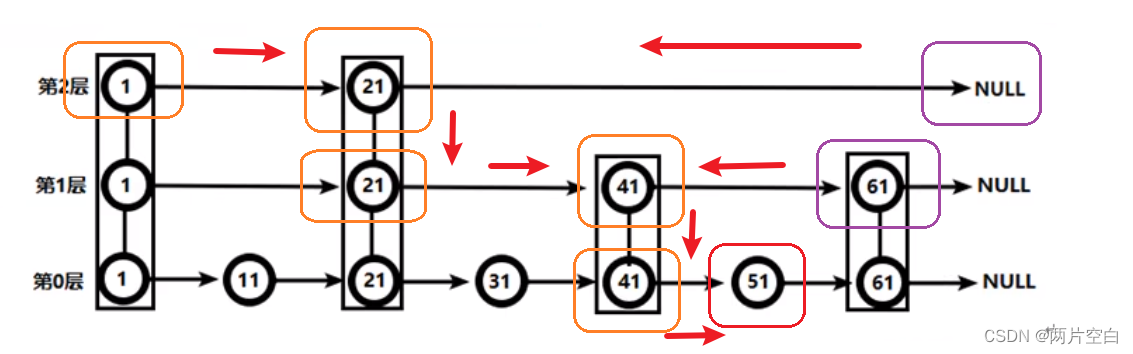
t 是前缀和数组，a 是原数组，建立如下的树状数组结构。

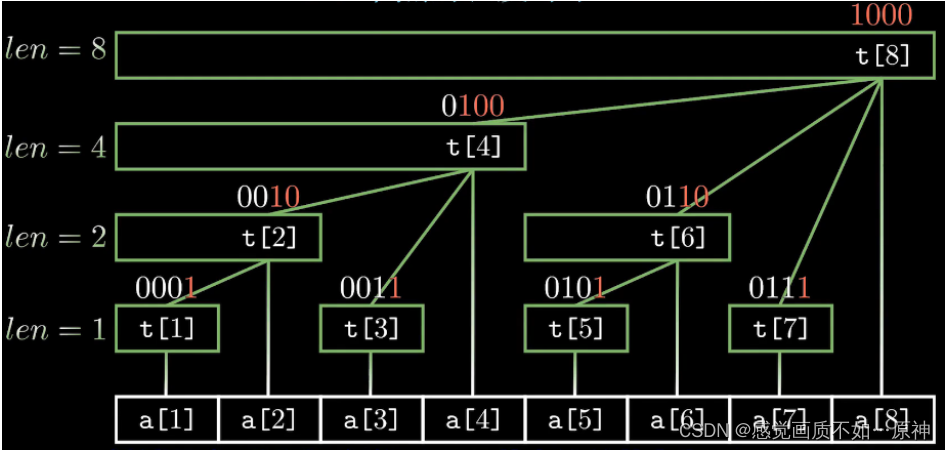
在这里插入图片描述
根据图我们可以发现：

$t [1] = a [1]$
$t [2] = t [1] + a [2]$
$t [3] = a [3]$
$t [4] = t [2] + t [3] + a [4]$
$t [5] = a [5]$
$t [6] = t [5] + a [6]$
$t [7] = a [7]$
$t [8] = t [4] + t [6] + t [7] + a [8]$

所以 t[8] 就是整个数组的前缀和。

此外还有：

每一个结点覆盖的长度都是 lowbit(x)（这个函数是求 x 二进制位的最后一位1，比如 x = 8，lowbit(x (1000) = 8,所以图中 t[8] 结点覆盖的长度是8；比如 x = 6,lowbit(6 (0110) ) = 2 ，所以图中 t[6] 结点覆盖的长度是2）。
t[x] 结点的父结点就是 t[x + lowbit(x)] (比如当 x = 1时，t[1] 的父结点为 t[1 + lowbit(0001) = 2 ]，t[2] 的父结点是 t[2 + lowbit(0010) = 4]；当 x = 5时，t[5] 的父结点为 t[5 + lowbit(0101) = 6]，t[6] 的父结点为 t[6 + lowbit(0110) = 8] )。

四、树状数组的操作

1. lowbit

根据其意思我们可以知道，这个函数就是求一个数的最低位的（这里的最低位指的是，最低位的1）。

那么我们要如何得到一个数 1 的最低位呢？

这里有一个数 x = 3，其二进制位是 0000 0011(只显示了低8位)
我们可以先将 x 取反，得到 ~x = 1111 1100
再将取反的 ~x + 1 = 1111 1101
最后将 x & (~x + 1) ，结果如下
0000 0011
1111 1101
0000 0001
我们发现如此一来就得到了 x 的最低位的1
实际上 (~x + 1) 就是 -x
所以 lowbit(x) 的操作相当于返回 x&(-x)

所以我们可以写出 lowbit 的代码：

int lowbit(int x){
    return x & (-x);
}

2. 单点修改

void add(int idx,int k)表示将数组中第 idx个数加上 k。

这里以 add(3,5)为例：

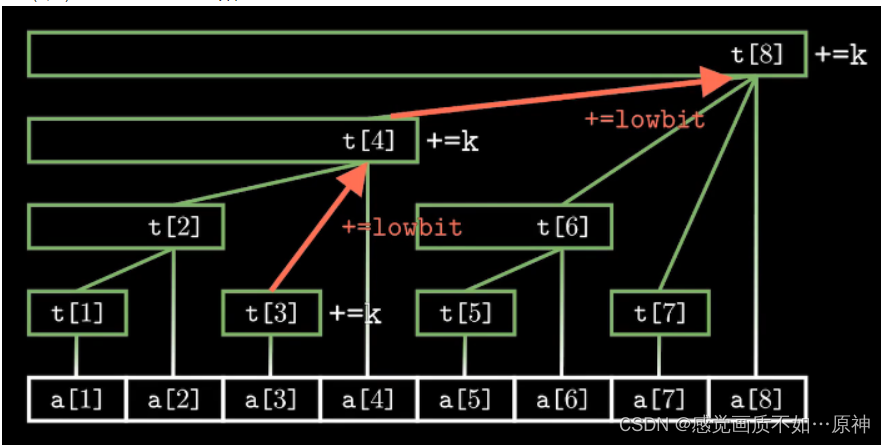
在这里插入图片描述
根据这张图可以发现：t[3] 影响了它的父结点 t[4],t[4] 又影响了它的父结点 t[8]。

所以如果我们要让 t[3] 加上 k，那么在这一条路径上的所有结点都要加上 k。之前我们已经知道了一个结点的父结点如何求，所以 add 的代码如下：

void add(int idx, int k)
{
    // i + lowbit(i)  就是结点 i 的父结点
    //我们要让这一条路径上的每一个点都加上 k
    for(int i = idx; i <= n; i += lowbit(i))
        t[i] += k;
}

3.求前缀和

int sum(int idx)求取前 idx个数的前缀和。

这里以 sum(7)为例：

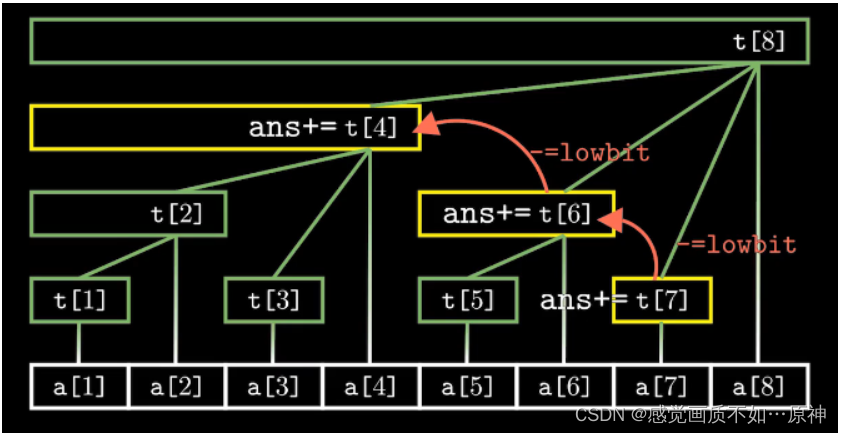
在这里插入图片描述
据图我们可以发现 $s u m (7) = t [7] + t [6] + t [4]$ ，我们观察 7(0111) , 6(0110) , 4(0100) 的二进制位可以发现，后面的一个数y 都等于前面的一个数 $x - l o w bi t (x)$ 。即 $7 - l o w bi t (7) = 6, 6 - l o w bi t (6) = 4, 4 - l o w bi t (4) = 0$ 。

我们可以写出如下的代码：

int sum(int idx)
{
    int ans = 0;
    for(int i = idx; i; i -= lowbit(i))
        ans += t[i];
    return ans;
}

五、例题

题目链接

P3374 【模板】树状数组 1

题目描述

如题，已知一个数列，你需要进行下面两种操作：

将某一个数加上 $x$
求出某区间每一个数的和

输入格式

第一行包含两个正整数 $n, m$ ，分别表示该数列数字的个数和操作的总个数。

第二行包含 $n$ 个用空格分隔的整数，其中第 $i$ 个数字表示数列第 $i$ 项的初始值。

接下来 $m$ 行每行包含 3 个整数，表示一个操作，具体如下：

1 x k 含义：将第 x 个数加上 k

2 x y 含义：输出区间 [x,y] 内每个数的和

输出格式

输出包含若干行整数，即为所有操作 2 的结果。

输入输出样例

输入

5 5
1 5 4 2 3
1 1 3
2 2 5
1 3 -1
1 4 2
2 1 4

输出

14
16

说明/提示

【数据范围】

$1≤n,m≤5×10^5$

直接套用模板即可，代码如下：

#include<iostream>
#include<algorithm>
#include<cmath>
using namespace std;

const int N = 5e5+10;
//c即前缀和数组 ，a 即原数组
int c[N],a[N],n,m;

int lowbit(int x){
    return x & -x;
}

void add(int x,int k){
    for(int i = x;i <= n;i += lowbit(i)) c[i] += k;
}

int sum(int x){
    int ans = 0;
    for(int i = x;i;i -= lowbit(i)) ans += c[i];
    return ans;
}

int main(){
    cin>>n>>m;
    for(int i = 1;i <= n;i++) scanf("%d",&a[i]);
    for(int i = 1;i <= n;i++) add(i,a[i]);
    
    while(m--){
        int op;
        scanf("%d",&op);
        if(op == 1){
            int x,k;
            scanf("%d%d",&x,&k);
            add(x,k);
        }
        else{
            int l,r;
            scanf("%d%d",&l,&r);
            //求具体某一区间和公式为 s(r) - s(l-1)
            cout<<sum(r) - sum(l-1)<<endl;
        }
    }
    return 0;
}