FSL训练过程一般都是最小化经验误差ERM。

    同时，由于现实任务的实际数据分布  是未知的，因此无法找到一个最优的参数组合 ，能最小化期望损失（最小值多少也是未知的），我们能做的实际上是尽可能的去找一个参数组合  逼近 。

    所以，必须设定一个假设空间（对应一个具体的模型，比如Vit，不同模型的假设空间不同），在这个假设空间里去寻找一个参数组合 ，它的期望损失能够逼近 ，当然，这个假设空间下的数据分布我们也是未知的，所以，我们做的只能是在这个假设空间下，使ERM损失 逼近 。

    根据误差分解的定义，总的误差可以分解为：

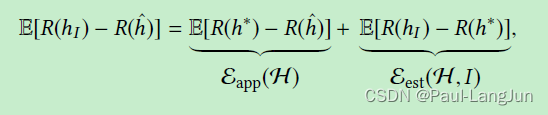
    可以看到，总误差受假设空间（模型）和训练集影响。因此，可以从模型、数据以及算法三个方面着手优化FSL。

     但是，FSL中的训练集一般很少。在有大量监督信息的情况下，第二项误差几乎可以忽略，但是FSL中这项误差是不可以忽略的，根源还是数据量太小，两种数据规模下误差的逼近情况如下图所示。

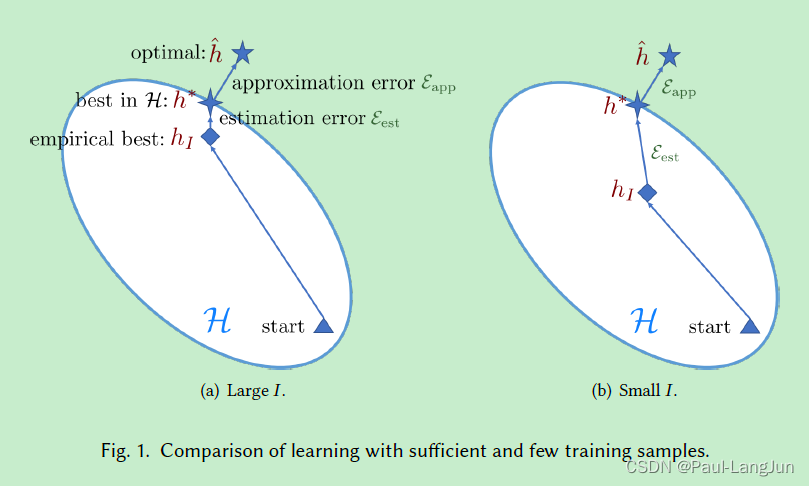
    可以看到，数据量充足情况下，误差逼近的会很好，但是在FSL这种情况下，误差逼近的就差强人意。