堆和优先级队列

一、堆

二、优先级队列

1、初识优先级队列

2、实现一个优先级队列

3、PriorityQueue

（1）实现了Comparable接口，重写了compareTo方法

（2）实现了Comparator接口，重写了compare方法

4、 PriorityQueue 的应用

Top-k问题：使用 PriorityQueue 来做

一、堆

堆是一种数据结构，是在完全二叉树的基础上进行了一些调整。
堆分为大根堆和小根堆，根结点比左右结点都大的堆叫做大根堆，根结点比左右结点都小的堆叫小根堆。
堆的存储结构（物理结构）：顺序存储，即会有一个数组，按照层序的方式顺序存储
若父结点下标为 i，则左孩子下标为 2*i+1，右孩子下标为2*i+2；若子结点下标为 i，则父结点下标为 (i-1)/2

二、优先级队列

1、初识优先级队列

优先级队列（PriorityQueue）底层是小根堆。

2、实现一个优先级队列

采用顺序存储的结构，使用数组来实现。

建堆的两种方法：建堆的时间复杂度是O(n)

1、先给elem数组赋值，创建一棵完全二叉树。然后从最后一棵子树的根结点开始调整，将每棵子树都调整成小根堆。调整的方案是向下调整（shiftDown）

shiftDown的时间复杂度：O(log n)

2、从无到有，不先创建完全二叉树，而是每放一个数据，都需要调整成小根堆。调整的方案是向上调整(shiftUp)

shiftUp的时间复杂度： O(log n)

对于优先级队列来说，入队和出队的时间复杂度 O(log n)

import java.util.Arrays;

//底层是小根堆
public class MyPriorityQueue {
    public int[] elem;
    public int size;//数组的有效长度
    public static final int DEFAULT_SIZE = 10;
    public MyPriorityQueue(){
        this.elem = new int[10];
    }
    /**
     * 2、建堆第二种方法：从无到有，不先创建完全二叉树，而是每放一个数据，都需要调整成小根堆。
     */
    public void createHeap2(int data){
        if(isEmpty()){
            elem[0] = data;
            size++;
            return;
        }
        if(isFull()){
            elem = Arrays.copyOf(elem,elem.length*2);
        }
        elem[size] = data;
        size++;
        shiftUp(size-1);
    }
    /**
     * 1、建堆第一种方法：先给elem数组赋值，创建一棵完全二叉树。然后从最后一棵子树的根结点开始调整，将每棵子树都调整成小根堆。
     */
    //给数组赋值，创建了一棵完全二叉树
    public void createTree(int[] arr){
        for (int i = 0; i < arr.length; i++) {
            this.elem[i] = arr[i];
            this.size++;
        }
    }
    //将完全二叉树调整成小根堆
    public void createHeap(){
        //从最后一个根结点开始往前调整
        int parent = ((size-1)-1)/2;
        for (int i = parent; i >= 0 ; i--) {
            shiftDown(i);
        }
    }
    //将根为parent的树调整为小根堆
    public void shiftDown(int parent){
        int child = 2*parent+1;
        while(child < size){
            //child+1 < size 保证有右树
            if(child+1 < size && elem[child+1] < elem[child]){
                child++;
            }
            //走到这，child 是左右子树最小值的下标
            if(elem[child] < elem[parent]){
                swap(child,parent);
                parent = child;
                child = 2*parent+1;
            }else{
                break;
            }
        }
    }
    public void swap(int x,int y){
        int tmp = elem[x];
        elem[x] = elem[y];
        elem[y] = tmp;
    }
    //入队：时间复杂度 O(log n)
    public void offer(int data){
        if(isFull()){
            elem = Arrays.copyOf(elem,elem.length*2);
        }
        elem[size] = data;
        size++;
        shiftUp(size-1);
    }
    public boolean isFull(){
        return size == this.elem.length;
    }
    public void shiftUp(int child){
        int parent = (child-1)/2;
        while(child > 0){
            if(elem[child] < elem[parent]){
                swap(child,parent);
                child = parent;
                parent = (child-1)/2;
            }else{
                break;
            }
        }
    }
    //出队：时间复杂度 O(log n)
    public int poll(){
        if(isEmpty()){
            return -1;
        }
        int delete = elem[0];
        swap(0,size-1);
        size--;
        //这样就只需要将parent=0的这棵树调整为小根堆就行了
        shiftDown(0);
        return delete;
    }
    public boolean isEmpty(){
        return size == 0;
    }
    //获取队顶元素但不删除
    public int peek(){
        if(isEmpty()){
            return -1;
        }
        return elem[0];
    }

}

3、PriorityQueue

PriorityQueue 底层是小根堆。
PriorityQueue 没有传数组容量时，默认的初始容量是11；如果传容量，不能<1，否则
会抛 IllegalArgumentException 异常

PriorityQueue 放入的数据必须得能比较大小，即插入的数据要么实现了Comparable<T>接口，要么实现了Comparator<T>接口，否则会抛出 ClassCastException异常
PriorityQueue 放入的数据如果实现了比较器，要把比较器传过去，优先使用比较器来比较
PriorityQueue 不能插入null对象，否则会抛出NullPointerException异常
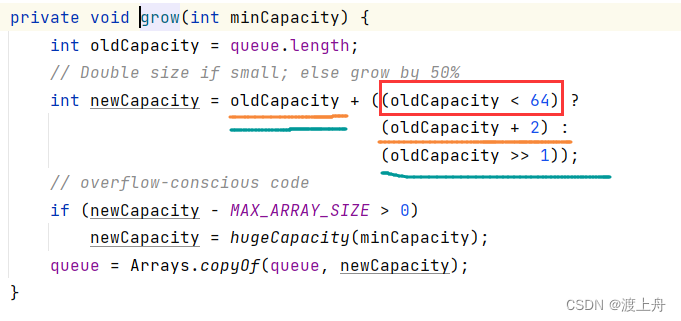
PriorityQueue 底层会自动扩容，容量<64时会2倍扩容，容量>=64时会1.5倍扩容

（1）实现了Comparable<T>接口，重写了compareTo方法

import java.util.PriorityQueue;
class Student implements Comparable<Student>{
    public int age;
    public Student(int age){
        this.age = age;
    }

    @Override
    public int compareTo(Student o) {
        return this.age - o.age;
    }
}
public class Test {
    public static void main(String[] args) {
        PriorityQueue<Student> priorityQueue = new PriorityQueue<>();
        priorityQueue.offer(new Student(20));
        priorityQueue.offer(new Student(10));
        priorityQueue.offer(new Student(30));
        System.out.println();
    }
}

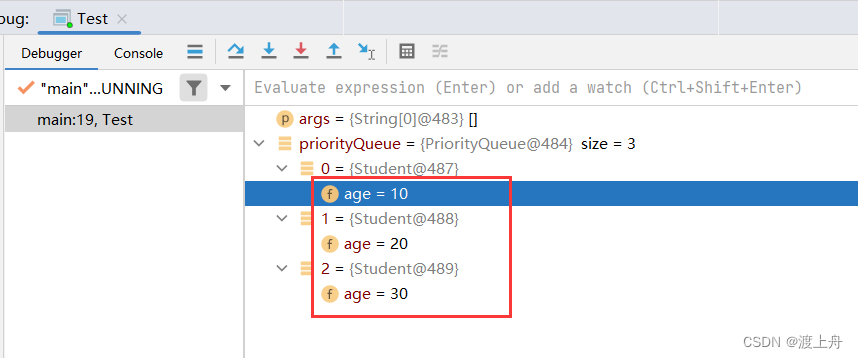
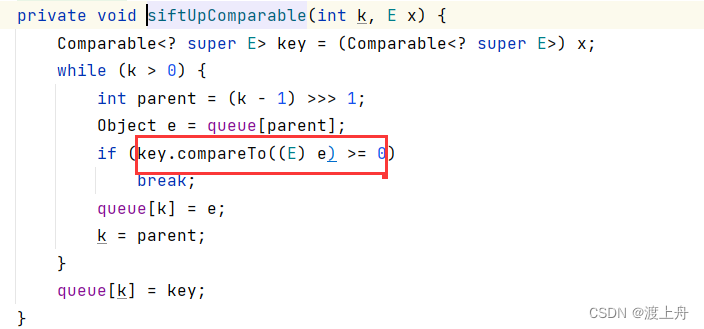
我们发现，数据确实有序了，而且是小根堆的形式。当然，我们也可以把它变成大根堆。

我们将 return this.age - o.age;改成 return o.age - this.age; 后，就变成了大根堆的形式。

（2）实现了Comparator<T>接口，重写了compare方法

那么，Integer怎么变成大根堆形式呢，Integer的compareTo方法是在源码里写好的，我们改不了源码。于是就用到了比较器，传个比较器过去，在比较器里重写compare方法，就可以改了。

class IntCmp implements Comparator<Integer>{
    @Override
    public int compare(Integer o1, Integer o2) {
        return o1.compareTo(o2);
    }
}
public class Test {
    public static void main(String[] args) {
        PriorityQueue<Integer> priorityQueue = new PriorityQueue<>(new IntCmp());
        priorityQueue.offer(20);
        priorityQueue.offer(10);
        priorityQueue.offer(30);
        System.out.println();
    }
}

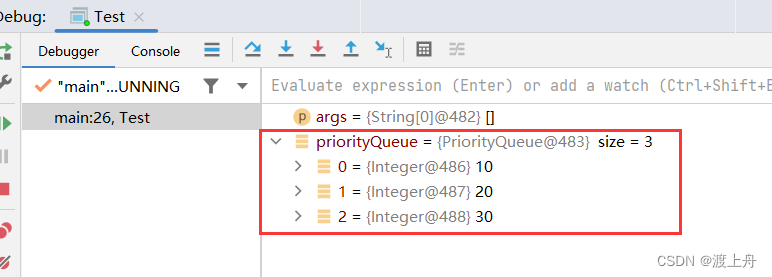
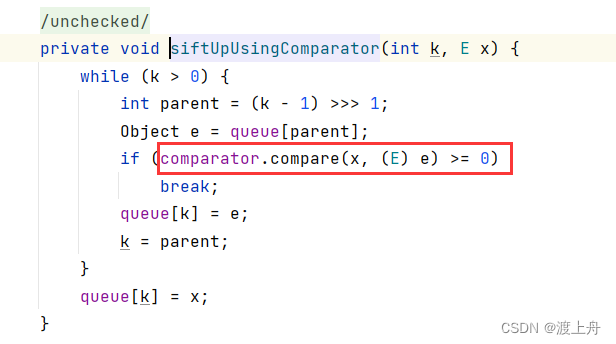
我们将 return o1.compareTo(o2);改成return o2.compareTo(o1);后，就变成了大根堆的形式。

4、 PriorityQueue 的应用

Top-k问题：使用 PriorityQueue 来做

求最大的前k个元素或第k大的元素，就将前 k 个数建立成小根堆；

求最小的前k个元素或第k小的元素，就将前 k 个数建立成大根堆。

时间复杂度：n*log k（堆的大小是k，数组中元素的个数是n）

（1）求数据集合中最大或最小的前k个元素（一般情况下，数据量都会非常大。）

如：找出数组中最小的k个数，以任意顺序返回这k个数均可。

解题思路：

将前 k 个数建立成大根堆
从第 k+1 个数据开始，每次都和堆顶元素比较，如果比堆顶元素小，就弹出堆顶元素，把这个元素放进堆
那么最后，堆中的这k个元素就是数组中最小的k个数

为什么找最小的k个数要建大根堆呢？

因为，大根堆的堆顶元素是最大的，

若后面的数据比它大，说明肯定不属于最小的k个数；若后面的数据比它小，说明它肯定不属于最小的k个数，那么就把它弹出，把这个数据放进去。以此类推。最后这个k大小的堆中就是最小的k个数了。

 //找出数组中最小的k个数
    public static int[] topK(int[] arr,int k){
        if(arr == null || k == 0) {
            return new int[0];
        }
        PriorityQueue<Integer> min = new PriorityQueue<>(new Comparator<Integer>() {
            @Override
            public int compare(Integer o1, Integer o2) {
                return o2.compareTo(o1);
            }
        });
        for (int i = 0; i < k; i++) {
            min.offer(arr[i]);
        }
        //到这里，建了一个大小为3的 大根堆
        for (int i = k; i < arr.length; i++) {
            int peek = min.peek();
            if(arr[i] < peek){
                min.poll();
                min.offer(arr[i]);
            }
        }
        //走到这，min 里就是数组中最小的k个数
        int[] tmp = new int[k];
        for (int i = 0; i < k; i++) {
            tmp[i] = min.poll();
        }
        return tmp;
}

（2）求第k小/第k大的元素

如：找出数组中第k小的元素

解题思路：

将前 k 个数建立成大根堆
从第 k+1 个数据开始，每次都和堆顶元素比较，如果比堆顶元素小，就弹出堆顶元素，把这个元素放进堆
那么最后，堆顶元素就是第k小的元素

//找出数组中第k小的数
    public static int least(int[] arr,int k){
        if(arr == null || k == 0) {
            return -1;
        }
        PriorityQueue<Integer> min = new PriorityQueue<>(new Comparator<Integer>() {
            @Override
            public int compare(Integer o1, Integer o2) {
                return o2.compareTo(o1);
            }
        });
        for (int i = 0; i < k; i++) {
            min.offer(arr[i]);
        }
        //到这里，建了一个大小为3的 大根堆
        for (int i = k; i < arr.length; i++) {
            int peek = min.peek();
            if(arr[i] < peek){
                min.poll();
                min.offer(arr[i]);
            }
        }
        //走到这，min 里就是数组中最小的k个数
        return min.peek();
}