什么是“DFS”

DFS 全称是 Depth First Search，中文名是深度优先搜索，是一种用于遍历或搜索树或图的算法。

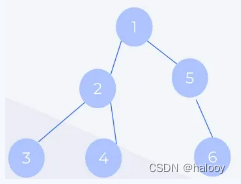
深度优先，就是每次都尝试向更深的节点走。

什么是“BFS”

BFS全称是 Breadth First Search，中文名是宽度优先搜索，也叫广度优先搜索。
其中的广度优先，就是每次都尝试访问同一层的节点， 如果同一层都访问完了，再访问下一层。

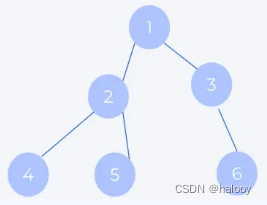
这样做的结果是，BFS 算法找到的路径是从起点开始的最短合法路径。换言之，这条路径所包含的边数最小。也就是说通过BFS算法只要找到目标节点，该路径就是最短路径。

为什么要用队列？

队列的原理是先进先出，而广度优先搜索类似于树的层次遍历，从离根节点最近的点开始向外扩散，因此用队列将最先遍历的点存入，后遍历的点后存入，符合bfs的逻辑。

首先我们先看BFS的节点处理顺序：
第一轮：处理根节点（第一层节点）
第二轮：处理根节点的所有子节点（第二层节点）
第三轮：处理距离根节点两步的所有节点（第三层节点）
…
然后我们对比队列的入队和出队顺序：
首先将根节点入队
第一轮：将根节点出队，对根节点进行处理，然后将所有的邻居（根节点的所有子节点）入队。但是新添加的节点不会立即遍历，而是在下一轮中处理。
结点的处理顺序与它们添加到队列的顺序是完全相同的顺序，即先进先出（FIFO）。这就是我们在 BFS 中使用队列的原因。

举例（走迷宫）：

主要思想就是需要定义一个队列，和一个标记数组，标记数组主要用来记录步数，并且判断是否走过（该节点是否已经处理过）。
首先将入口坐标入队，并且将入口坐标在标记数组的值改为0（表示当前0步）
其次进入循环，将入口坐标进行出队，然后上下左右遍历，当相邻节点符合条件时将该节点入队，并且更新该节点在标记数组的值+1（表明当前距离起点有1步）。再进行判断该节点是否等于出口。如果等于直接返回当前步数。
然后再进行循环，对相邻节点。因为队列的特性，优先处理的都是相邻节点。
因此当找到出口位置时，就是最优路径。

#include <iostream>
#include <bits/stdc++.h>
using namespace std;

typedef pair<int, int> PII;
// 定义地图
int ditu[110][110];
// 标记节点，没走过的初始化为-1，走过的标记为1
int label[110][110];
// 定义地图大小，N行M列 
int N, M;
// 定义坐标入口x_r,y_r，出口x_c,y_c
int x_r, y_r, x_c, y_c;
// 定义队列
queue<PII> q;

// 广度优先搜索
int bfs()
{
  // 初始化标记数组
  memset(label, -1, sizeof(label));
  label[x_r][y_r] = 0;
  // 将即将搜索的节点压入队列
  q.push({x_r, y_r});
  // 定义上下左右
  int x_move[4] = {-1, 0, 1, 0}, y_move[4] = {0, 1, 0, -1};
  // 当队列不为空时则路径没有全部遍历结束,为空说明地图全部走完
  while(q.size())
  {
    // 将节点取出
    auto head = q.front();
    q.pop();
    // 将该节点进行移动
    for(int i=0; i<4; i++)
    {
      // 更新移动后的位置
      int x = head.first + x_move[i];
      int y = head.second + y_move[i];
      // 对更新后的位置进行判断
      // 满足在边界内，该位置没有障碍物，该位置没有走过（没有被标记过）
      if(x>=1 && x <= N && y>=1 && y<=M && ditu[x][y]==1 && label[x][y]==-1)
      {
        // 记录步数，当前节点与入口的距离
        label[x][y] = label[head.first][head.second] + 1;
        // 给当前节点入队，在下次循环时以该节点为起始进行上下左右
        q.push({x,y});
        // 判断当前位置是否是出口，如果是则返回步数
        if(x==x_c && y==y_c)
        {
          return label[x][y];
        }
      }
    }
  }
  // 如果所有节点都遍历结束都没有出口，则返回-1
  return -1;
}
int main()
{
  // 输入地图大小
  cin >> N >> M;
  for(int i=1; i<=N; i++)
  {
    for(int j=1; j<=M; j++)
    {
      cin >> ditu[i][j];
    }
  }
  cin >> x_r >> y_r >> x_c >> y_c;
  cout << bfs();
  return 0;
}