如果还没有做过前面的题，建议先去尝试动态规划8

1218. 最长定差子序列

如果对之前的题比较熟悉的话，比较容易直接这样写，但是这样会超出时间限制：

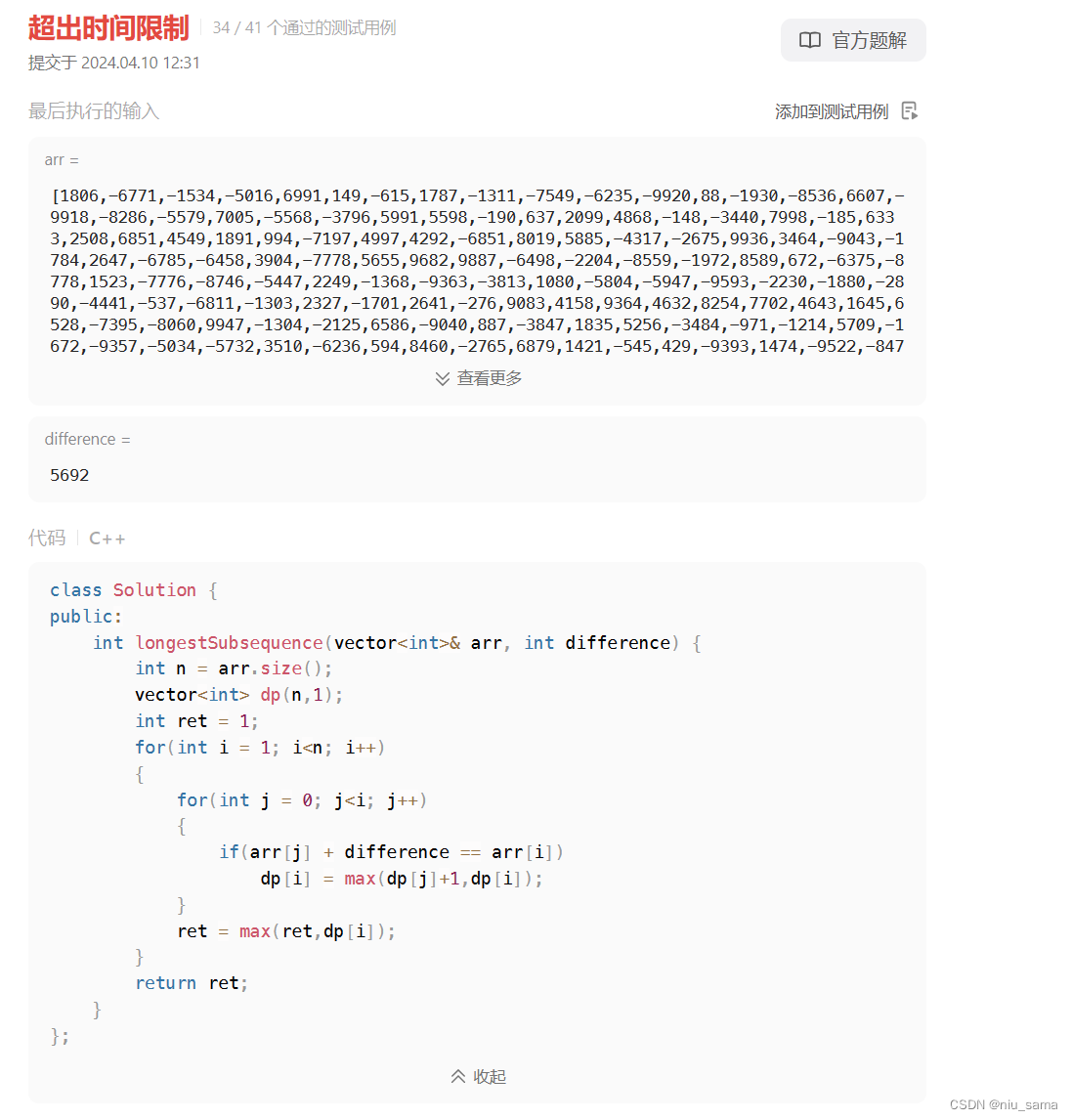
所以我们要变成一次遍历，就得倒着推，就像这样：

使dp[i] 表示以 i 为结尾的最长等差子序列的长度。
然后我们通过使用哈希表来进行优化：

1. unordered_map<int,int> hash; 对应的是 arr[i] 和 dp[i] ，相当于直接对哈希表进行动态规划
2. 根据状态转移可以得到：hash[arr[i]] = hash[arr[i] - difference] + 1;

class Solution {
public:
    int longestSubsequence(vector<int>& arr, int difference) {
        unordered_map<int,int> hash;  //arr[i] -- dp[i]

        int ret = 0;
        for(int i = 0; i<arr.size(); i++)
        {
            hash[arr[i]] = hash[arr[i] - difference] + 1;
            ret = max(ret,hash[arr[i]]);
        }
        return ret;
    }
};

873. 最长的斐波那契子序列的长度

思路：

1. 经验+题目要求
   dp[i]表示：以 i 位置为结尾的所有子序列中，最长的斐波那契子序列长度。error

这样只能固定最后一个数，这样是解决不了问题的。固定最后两个数可以知道前面所有数。

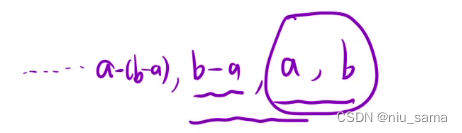
dp[i][j]表示：以 i 位置以及 j 位置为结尾的所有子序列中，最长的斐波那契子序列长度

2. 状态转移方程
   

3. 初始化
   表里面所有值都初始化为2。

4. 填表顺序
   从上往下

5. 返回值
   dp表最大值ret，ret < 3 ? 0 : ret;

class Solution {
public:
    int lenLongestFibSubseq(vector<int>& arr) {
        int n = arr.size();
        //优化
        unordered_map<int,int> hash;
        for(int i = 0; i<n; i++) hash[arr[i]] = i;
        
        int ret = 0;
        vector<vector<int>> dp(n,vector<int>(n,2));
        for(int j = 2; j<n; j++)//固定最后一个位置
        {
            for(int i = 1; i<j; i++)//固定倒数第二个位置
            {
                int a = arr[j] - arr[i];
                if(hash.count(a) && a < arr[i])
                    dp[i][j] = dp[hash[a]][i] + 1;

                ret = max(ret,dp[i][j]);
            }
        }
        return ret < 3 ? 0 : ret;
    }
};

1027. 最长等差数列

思路：

1. 经验+题目要求

dp[i][j]表示：以 i 位置以及 j 位置为结尾的所有子序列中，最长的斐波那契子序列长度

2. 状态转移方程

对于优化：
我们选择第二种优化，因为效率更高。

3. 初始化
   dp表里面所有值都初始化为2
4. 填表顺序
   先固定倒数第二个数，然后枚举最后一个数。

class Solution {
public:
    int longestArithSeqLength(vector<int>& nums) {
        int n = nums.size();
        //优化
        unordered_map<int,int> hash;
        hash[nums[0]] = 0;
        //for(int i = 0; i<n; i++) hash[nums[i]] = i;
        
        int ret = 2;
        vector<vector<int>> dp(n,vector<int>(n,2));
        for(int i = 1; i<n; i++)//固定倒数第二个位置
        {
            for(int j = i+1; j<n; j++)//固定倒数第一个位置
            {
                int a = 2*nums[i] - nums[j];
                if(hash.count(a))
                    dp[i][j] = dp[hash[a]][i] + 1;

                ret = max(ret,dp[i][j]);
            }
            hash[nums[i]] = i;
        }
        return ret;
    }
};