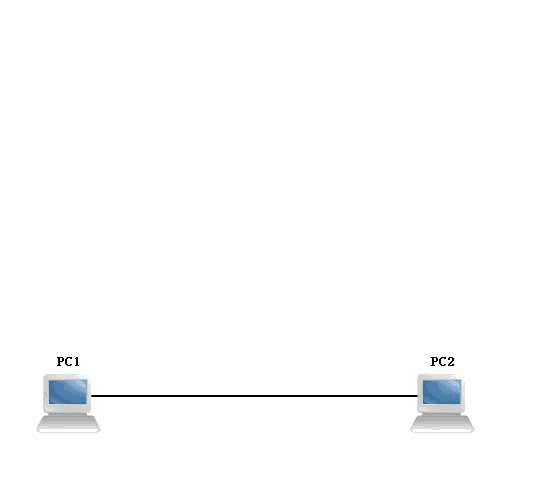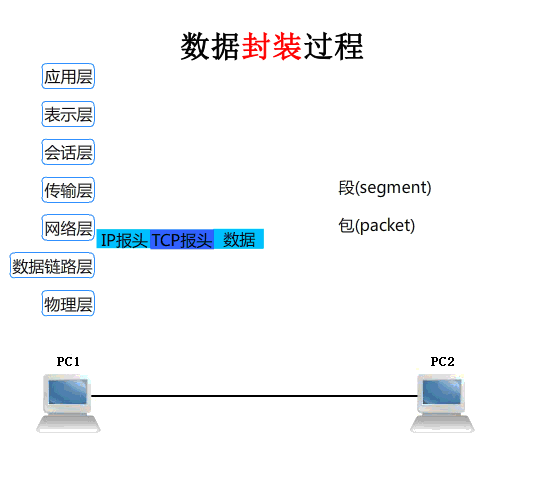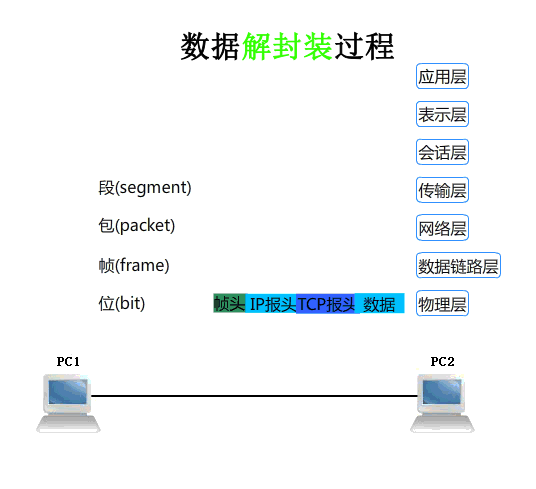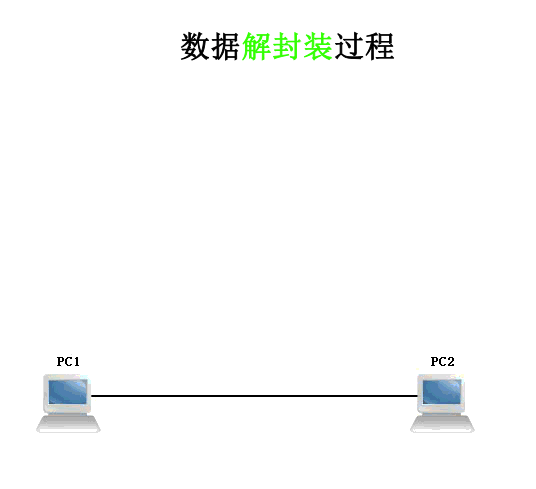
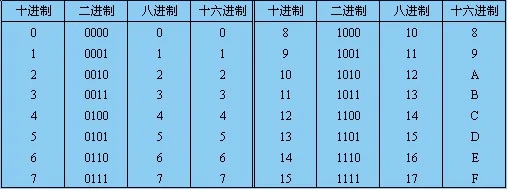
注： 本系列仅为个人学习笔记，学习内容为《算法小讲堂》（视频传送门），通俗易懂适合编程入门小白，需要具备python语言基础，本人小白，如内容有误感谢您的批评指正

梅森数（Mersenne Prime）指的是形如$2^n-1$的正整数，其中指数n是素数，如果结果是一个素数，则称其为梅森素数
例如$2^2-1=3$ ,$2^3-1=7$都是梅森素数，n 为 2，3，5，7 时，结果都是梅森素数，但是当 n 为 11 时，$2^{1}1-1=2047=23\times 89$，可以拆分就不是梅森素数,所以并不是所有指数为素数的情况都是梅森素数。

那么让我们用代码找出指数n<22的所有梅森素数该怎么实现呢？思路很简单！判断指数是不是素数然后在判断$2^n-1$是不是素数即可。

def prime(num):
    i = 2
    while i<= math.sqrt(num):
        if num%i==0:
            return 0
        i += 1
    return 1

print('指数n<22的梅森素数为：')
count = 0
for i in range(2,22):
    if prime(i):
        if prime(2**i-1):
            print(2**i-1)
            count += 1
print('22以内的梅森素数共有{}个'.format(count))

输出结果

指数n<22的梅森素数为：
3
7
31
127
8191
131071
524287
22以内的梅森素数共有7个

在前面学习完了一些内容之后，素数大家一定都已经掌握了，让我们升级一下来看看著名的歌德巴赫猜想！

哥德巴赫猜想（Goldbach’s conjecture）是数论中存在最久的未解问：用现代的数学语言，哥德巴赫猜想可以陈述为：任一大于 2 的偶数，都可表示成两个素数之和。

这个猜想与当时欧洲数论学家讨论的整数分拆问题有一定联系。整数分拆问题是一类讨论“是否能将整数分拆为某些拥有特定性质的数的和”的问题。比如能否将所有整数都分拆为若干个完全平方数之和，或者若干个完全立方数的和等。而将一个给定的偶数分拆成两个素数之和，则被称之为此数的哥德巴赫分拆。

例如：

4 = 2 + 2
6 = 3 + 3
8 = 3 + 5
10 = 3 + 7 = 5 + 5
12 = 5 + 7
14 = 3 + 11 = 7 + 7

那么让我们来验证验证歌德巴赫猜想对 2333 以内的正偶数都是成立的，即2333以内的不小于4的正偶数都能够分解为两个素数之和，实现思路当然也很简单啦就是将整数分解为两个正整数，再判断这两个正整数是否都为素数，输出最小的一组分解结果即可代码实现如下

def prime(num):
    i = 2
    while i <= math.sqrt(num):
        if num%i==0:
            return 0
        i += 1
    return 1

if __name__=='__main__':
    while True:
        num = int(input('请输入一个不小于4的正偶数，退出输入0：'))
        if num==0:
            print('已退出！')
            break
        elif num%2!=0 or num < 4:
            print('输入不合法请重新输入！')
            print()
            continue
        i = 2
        while i <= num//2:
            if prime(i)and prime(num-i):
                print('分解结果：{}\t{}'.format(i,num-i)) 
                print()
                break
            i += 1

输出结果：

请输入一个不小于4的正偶数，退出输入0：2
输入不合法请重新输入！

请输入一个不小于4的正偶数，退出输入0：9
输入不合法请重新输入！

请输入一个不小于4的正偶数，退出输入0：18
分解结果：5	13

请输入一个不小于4的正偶数，退出输入0：300
分解结果：7	293

请输入一个不小于4的正偶数，退出输入0：0
已退出！