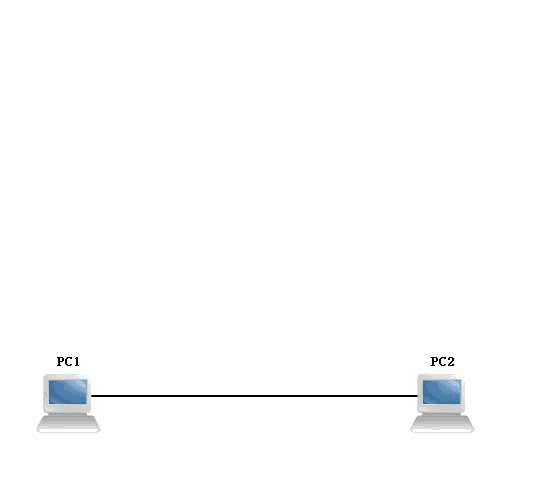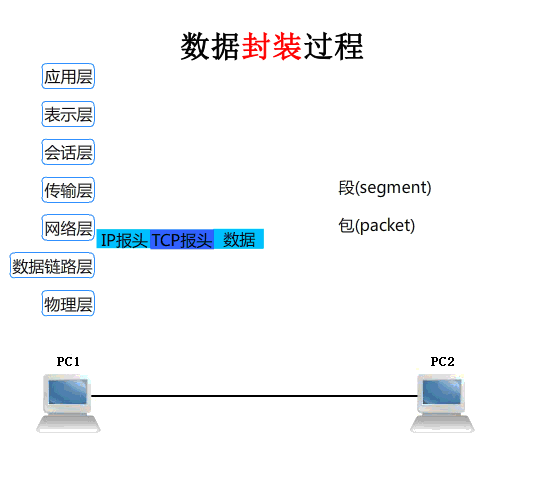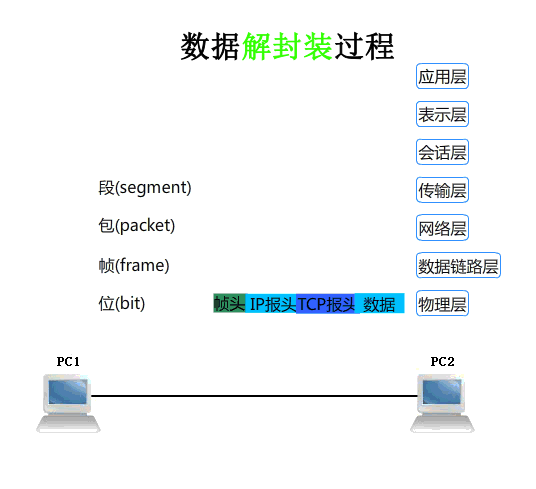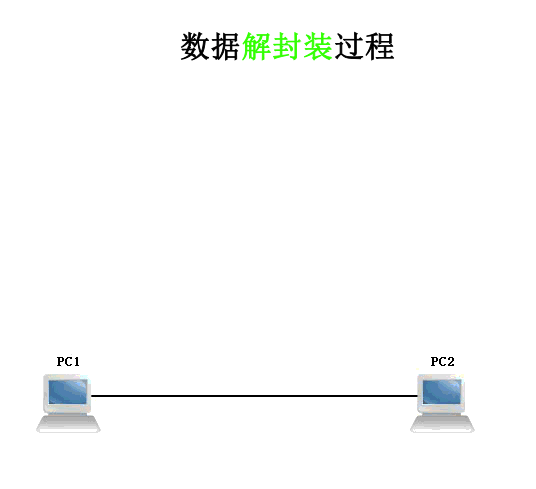
相机模型
文章目录
- 相机模型
- 四个坐标系
- 针孔相机模型
- 世界坐标系到相机坐标系
- 相机坐标系到图像坐标系
- 图像坐标到像素坐标
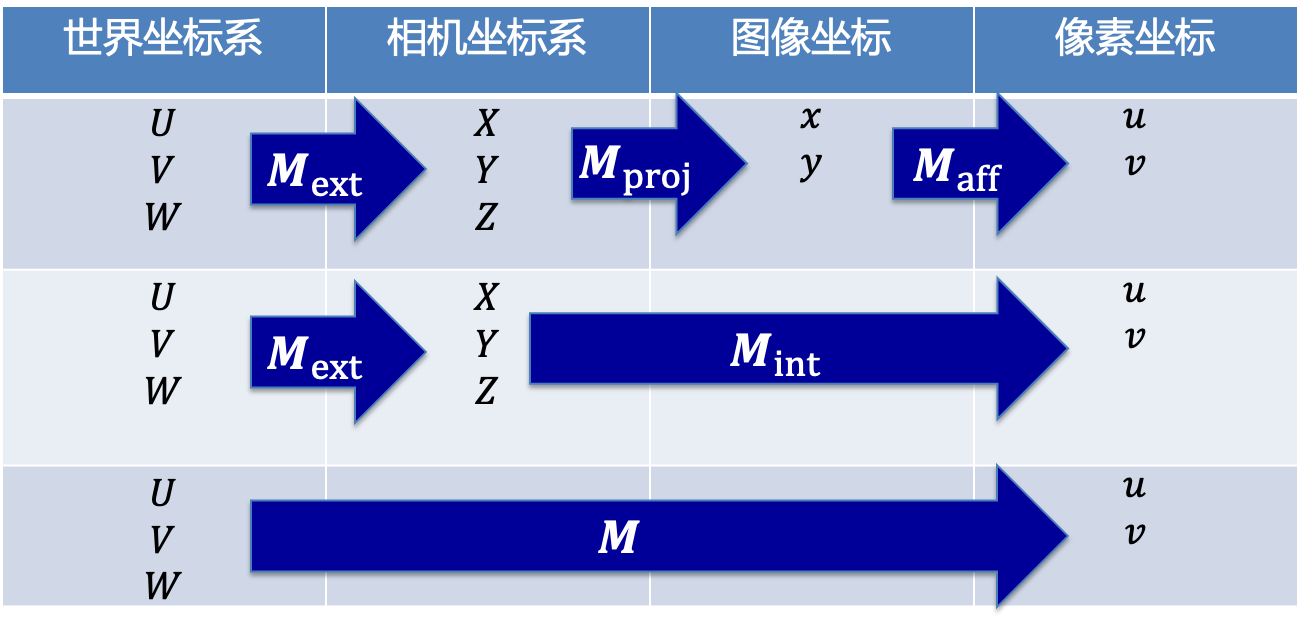
四个坐标系
①世界坐标系:是客观三维世界的绝对坐标系,也称客观坐标系。因为数码相机安放在三维空间中,我们需要世界坐标系这个基准坐标系来描述数码相机的位置,并且用它来描述安放在此三维环境中的其它任何物体的位置,用 ( X w , Y w , Z w ) (X_w, Y_w, Z_w) (Xw,Yw,Zw)表示其坐标值。
②相机坐标系(光心坐标系):以相机的光心为坐标原点,X 轴和Y 轴分别平行于图像坐标系的 X 轴和Y 轴,相机的光轴为Z 轴,用 ( X c , Y c , Z c ) (X_c, Y_c, Z_c) (Xc,Yc,Zc)表示其坐标值。
③图像坐标系:以CCD 图像平面的中心为坐标原点,X轴和Y 轴分别平行于图像平面的两条垂直边,用 ( x , y ) ( x , y ) (x,y)表示其坐标值。图像坐标系是用物理单位(例如毫米)表示像素在图像中的位置。
④像素坐标系:以 CCD 图像平面的左上角顶点为原点,X 轴和Y 轴分别平行于图像坐标系的 X 轴和Y 轴,用 ( u , v ) (u , v ) (u,v)表示其坐标值。
针孔相机模型
相机实质上就是完成一个3D空间到2D平面的投影的过程其中投影中心称为摄像机中心 ,也称为光心摄像机中心到图像平面的垂线称为摄像机的主轴或主射线 ,而主轴在图像平面的交点称为主点。过摄像机中心平行于图像平面的平面称为摄像机的主平面。

世界坐标系到相机坐标系

一般, 空间点采用不同的欧氏坐标系表示 ,称为世界坐标系。其中世界坐标系于相机坐标系通过旋转和平移相联系
因为可以将相机坐标系看作世界坐标系的一个欧式变换,设一个点
A
A
A在世界坐标系中的坐标为
[
X
w
,
Y
w
,
Z
w
,
1
]
T
[X_w,Y_w,Z_w,1]^T
[Xw,Yw,Zw,1]T,在相机坐标系中的坐标为
[
X
c
,
Y
c
,
Z
c
,
1
]
T
[X_c,Y_c,Z_c,1]^T
[Xc,Yc,Zc,1]T,则存在以下关系
[
X
c
Y
c
Z
c
1
]
=
[
R
t
0
T
1
]
[
X
w
Y
w
Z
w
1
]
\begin{bmatrix} X_c\\ Y_c\\ Z_c\\ 1 \end{bmatrix}= \begin{bmatrix} R&t\\ 0^T&1 \end{bmatrix} \begin{bmatrix} X_w\\ Y_w\\ Z_w\\ 1 \end{bmatrix}
XcYcZc1
=[R0Tt1]
XwYwZw1
其中
R
,
t
R,t
R,t称为相机的外部参数,并将
[
R
t
0
T
1
]
\begin{bmatrix} R&t\\ 0^T&1 \end{bmatrix}
[R0Tt1]即为
M
e
x
t
M_{ext}
Mext
相机坐标系到图像坐标系
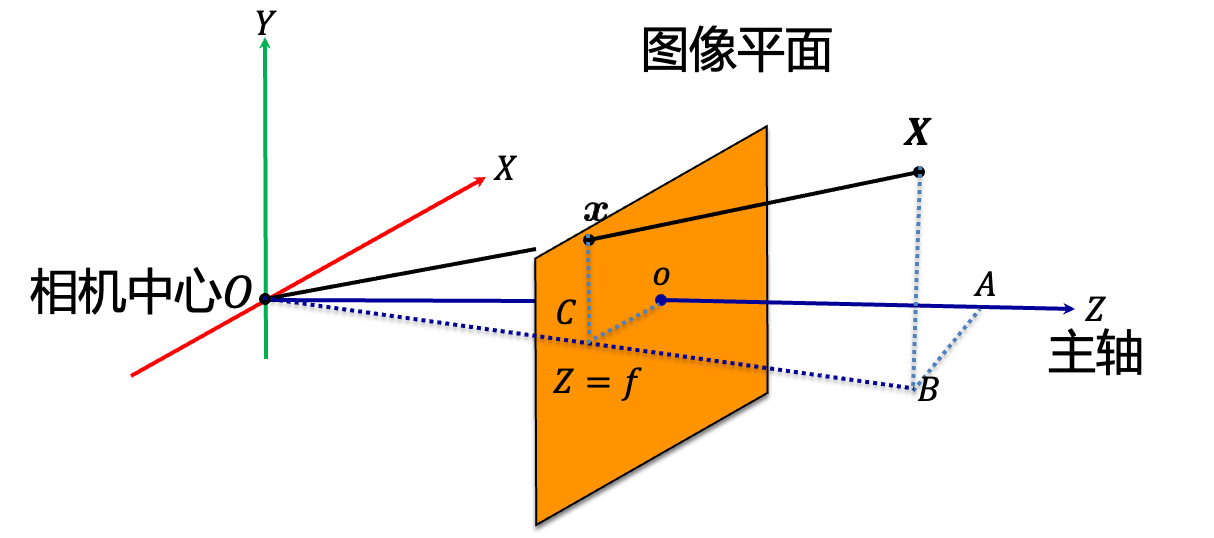
根据相似三角形可得 ∥ O C ∥ ∥ A B ∥ = ∥ O O ∥ ∥ O A ∥ = ∥ O C ∥ ∥ O B ∥ = ∥ x C ∥ ∥ X B ∥ \frac{\|OC\|}{\|AB\|}=\frac{\|OO\|}{\|OA\|}=\frac{\|OC\|}{\|OB\|}=\frac{\|xC\|}{\|XB\|} ∥AB∥∥OC∥=∥OA∥∥OO∥=∥OB∥∥OC∥=∥XB∥∥xC∥
可得在相机坐标系中的点 ( X c , Y c , Z c ) (X_c,Y_c,Z_c) (Xc,Yc,Zc)在图像平面上的投影为 ( f X c Z c , f Y c Z c ) (f\frac{X_c}{Z_c},f\frac{Y_c}{Z_c}) (fZcXc,fZcYc),其中在齐次坐标中表示为 ( f X c , f Y c , Z c ) (fX_c,fY_c,Z_c) (fXc,fYc,Zc)
可构造方程
[
f
X
c
f
Y
c
Z
c
]
=
[
f
0
f
0
1
0
]
[
X
c
Y
c
Z
c
1
]
\begin{bmatrix} fX_c\\ fY_c\\ Z_c \end{bmatrix} =\begin{bmatrix}f&&&0\\&f&&0\\&&1&0\end{bmatrix}\begin{bmatrix}X_c\\Y_c\\Z_c\\1\end{bmatrix}
fXcfYcZc
=
ff1000
XcYcZc1
其中矩阵
[
f
0
f
0
1
0
]
\begin{bmatrix} f&&&0\\ &f&&0\\ &&1&0 \end{bmatrix}
ff1000
记为
M
p
r
o
j
M_{proj}
Mproj
图像坐标到像素坐标
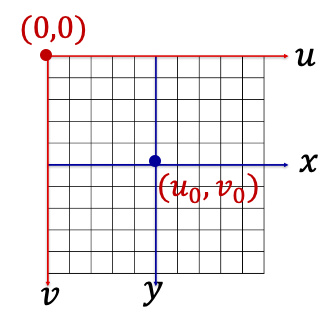
可得以下关系
[
u
v
1
]
=
[
k
u
0
l
v
0
1
]
[
x
y
1
]
\begin{bmatrix} u\\ v\\ 1 \end{bmatrix} =\begin{bmatrix} k&&u_0\\ &l&v_0\\ &&1 \end{bmatrix} \begin{bmatrix} x\\ y\\ 1 \end{bmatrix}
uv1
=
klu0v01
xy1
其中
k
k
k和
l
l
l分别是每个像素在图像平面x和 y方向上的物理尺寸。
其中将矩阵 [ k u 0 l v 0 1 ] \begin{bmatrix} k&&u_0\\ &l&v_0\\ &&1 \end{bmatrix} klu0v01 记为 M a f f M_{aff} Maff

若 u , v u,v u,v不垂直,其夹角为 θ \theta θ。则 M a f f = [ k − k cos θ u 0 l / sin θ v 0 1 ] M_{aff}=\begin{bmatrix} k&-k\cos\theta&u_0\\ &l/\sin\theta&v_0\\ &&1 \end{bmatrix} Maff= k−kcosθl/sinθu0v01