前言

和上一篇文章一样，这篇文章是介绍蓝桥杯中的第二种暴力算法就是DFS算法，在蓝桥杯中非常常用。

简单介绍

DFS算法中文名就是深度优先算法，在这里就不详细介绍这个算法了，可以自行搜索，网上有很多，或者可以看看我写的这篇文章：以题为例浅谈DFS算法-CSDN博客

话不多说直接上题

小朋友崇拜圈

题目链接：用户登录

题意

班里 NN 个小朋友，每个人都有自己最崇拜的一个小朋友（也可以是自己）。

在一个游戏中，需要小朋友坐一个圈，每个小朋友都有自己最崇拜的小朋友在他的右手边。

求满足条件的圈最大多少人？

小朋友编号为 1,2,3,⋯N1,2,3,⋯N。

输入描述

输入第一行，一个整数 N（3<N<105）N（3<N<105）。

接下来一行 NN 个整数，由空格分开。

输出描述

要求输出一个整数，表示满足条件的最大圈的人数。

输入

9
3 4 2 5 3 8 4 6 9

输出

4

 解释

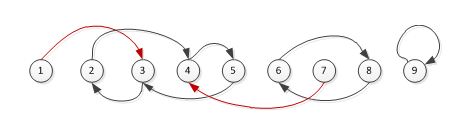
如下图所示，崇拜关系用箭头表示，红色表示不在圈中。

显然，最大圈是[2 4 5 3] 构成的圈。

先上代码

#include<stdio.h>
long long n;
long long a[100005];
long long t;
long long max=0;
long long v[100005]; 
void dfs(long long x,long long y)
{
	if(v[x])  //当v[x]为1的时候说明这个点已经遍历过了，说明是从一个未遍历过的一个点，又比遍历回来
	{
		if(a[x]==a[t])  //只有当这一个遍历回来的点等于初始值时才能说明它组成一个圈 
		{
			if(max<y)
			max=y;  //去动态的增长长度
		}
		return;
	}
	else
	{
		v[x]=1;  //就是如果这个点没有遍历过现在已经遍历过了
		dfs(a[x],y+1); 在以这个点为起点去继续遍历
		v[x]=0;  //如果不行的话全部回溯为0，为下一次遍历做好准备
	}
}
int main()
{
	scanf("%d",&n);
	for(long long i=1;i<=n;i++)
	{
		scanf("%d",&a[i]);
	}  //输入，就不解释了
	for(int i=1;i<=n;i++)
	{
		t=i;  //用t去记录初始值，也就是说以这个点为起步看看能不能组成一个圈；
		dfs(i,0); //i代表一个一个点去遍历，看看能不能组成一个圈，0代表这个圈的长度
	}
	printf("%d",max);
	
} 

在这里一定要注意一个点就是一个小朋友只能有一个崇拜者，所以它门最多只能形成一个圈，不会说会有圈中圈