2011年认证杯SPSSPRO杯数学建模
B题 生物多样性的评估
原题再现:
2010 年是联合国大会确定的国际生物多样性年。保护地球上的生物多样性已经越来越被人类社会所关注,相关的大规模科研和考察计划也层出不穷。为了更好地建立国际交流与专家间的合作,联合国还建立了生物多样性和生态系统服务政府间科学政策平台(IPBES)。但迄今为止,几乎所有的考察计划都面临着一个基本的困难:如何评价被考察区域的生物多样性。传统的方法是清点物种数量,但现在有许多科学家认为这种方法具有很大的局限性。譬如有人提出应当考虑物种的相似程度。有人则提出有一些物种的基因多样性程度远远超过另一些物种,所以应当考虑基因的多样性等。但现在还缺少一种能全面考虑不同因素的对生物多样性进行测定的方法。
第一阶段问题:
问题: 请你建立合理的数学模型,设计一个全面而有效的评价生物多样性的指标,以利于今后考察和科研工作的开展。
整体求解过程概述(摘要)
本文建立了人工神经网络和模糊综合评价两个指标模型。生物多样性包括 3 个主要因素及 13 个二级因素,量化这些因素来确定最终的生物多样性评价指标。
合理评价指标的确定关键在于各因素权重的确定,结合人工神经网络的自学习和自适应能力,我们首先建立了基于人工神经网络的评价指标,通过 BP 神经网络对样本进行训练,不断调整评价因素对评价指标的权重,以使各因素对目标的权重达到最优,进而得到理想的评价标准。
生物多样性评价中各因素是抽象、定性的,通过对某一地区的考察,无法给出某个因素具体的量化数据情况,只能模糊评价该因素的情况是恶劣还是良好。鉴于生物多样性评价模型的层次性,提出模糊综合评价指标。模糊综合评价的模型中,由于评价因素的抽象性和难以量化性,我们利用层次分析法得到各因素对目标的权重,将评测人员对各因素感性的认识转化为具体的权重数值,同时减少由于评价人员主观因素对结果造成的影响,为模糊综合评判指标的确定提供了权值基础。该模型还将对各因素的认识划分为 5 个等级 ,运用偏大柯西分布隶属函数对各等级进行量化,得到其评语的量化值。根据具体情况,对各项二级因素打分,结合由偏大柯西分布的隶属函数确定的单项评语的量化值确定模糊评判集,再根据模糊评判理论,由各因素权值和模糊评判集得到生物多样性的评估指数。
在少量数据基础上,基于专家打分趋向正态分布的事实,我们模拟了专家考察团的评判,检验了模糊综合评价指标的全面性和有效性。文章最后对两种模型进行了比较,并对实际生物多样性评价给出两点建议,以利于今后考察和科研工作的开展。
问题分析:
传统的生物多样性评价方法只是清点物种数量。但是,生物多样性包括遗传多样性、物种多样性和生态系统多样性三个层次和水平1。遗传多样性是指蕴藏在生物体基因中的遗传信息的综合,因此对其测度是比较复杂的,但总体上对于遗传基因的特征表现主要考虑种型情况、特有情况和古老残遗情况三个方面。
物种多样性是地球上现有生物有机体种的复杂多样性,包括群落种的物种数、总个体数、物种的多度和均匀度等。统计物种数是被最为广泛采用、也是最为简单的生物评价方法。但是,单纯以物种数作为评价标准具有较大片面性,考察某一地区的物种多样性还必须考虑到物种的相对丰度,即相对于这一地区的各个群落内,某种或某一类群生物的个体数量的估量。同时,随着生态环境遭到破坏,有很多物种处于濒危状态,这些物种的情况对于考察相应地区的生物多样性也有着举足轻重的作用,所以,生物多样性评价还不得不考虑某一地区的物种濒危程度。从宏观上,生物种群的稳定性对于考察某一地区的生物多样性也是至关重要的。最后,生物多样性日益受到人类生活的影响,全面的评价也必须把人类的威胁考虑进去。
生态系统多样性是指生物圈内生境、生物群落和生态学过程的多样化。是从宏观上考察生物多样性的必要手段,包括群落的组成、结构和动态。它是物种多样性的宏观与抽象。在认真领会其概念的基础上,列出以下指标对生态系统多样性进行评价,即生境类型多样性、生境稀有性、自然性、面积适宜性、生态系统稳定性。
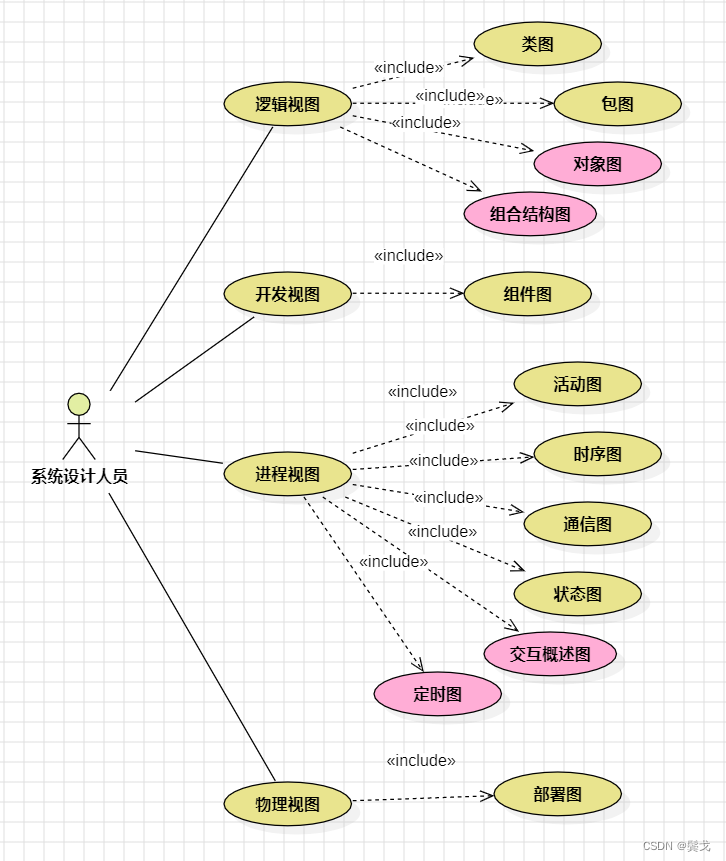
综上,将生物多样性的评价指标归纳于图 1(3 个主因素与 13 个子因素)。这三者相辅相成,相互包容且相互关联,因此,全面而有效地评价生物多样性离不开综合考虑这三个方面的内容。

论文缩略图:


全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可
部分程序代码:(代码和文档not free)
count=[1,2,3,4,5,6,7,8,9,10,11,12,13,14];
for i=1 : size(m_data,1)
for j=1 : 13
m_data(i,j)=((m_data(i,j)-min(m_data(:,j),[],1))/(max(m_data(:,j),[],
1)-min(m_data(:,j),[],1)));
end
end
Count=70;
%定义网络输入 p 和期望输出 t
p1=m_data(1:Count,1:13);
t1=m_data(1:Count,14);
p=p1';t=t1';
%设置网络隐单元的神经元数(5~30 验证后 10 个最好)
n=30;
%建立相应的 BP 网络
net=newff(minmax(p),[n,1],{'tansig','purelin'},'trainlm');
%对没有训练的网络仿真
y1=sim(net,p);
%绘制仿真得到的曲线
%figure
%plot(t);
%hold on
%plot(y1,'r:')
%legend('真实值','估计值');
%title('没有训练的 BP 网络模型输出拟合曲线');
%xlabel('输入样本点');
%ylabel('汽车保有量');
%hold off
%训练网络
net.trainParam.epochs=2000;
net.trainParam.lr=0.05;
net.trainParam.goal=0.005;
net=train(net,p,t);
%对训练后的网络进行仿真
y=sim(net,p);
%绘出训练后的仿真结果
%net.IW{1,1} % 输入层到隐层的权值
%net.b{1,1} % 输入层到隐层的阈值
%net.IW{2,1} % 隐层到输出层的权值
%net.b{2,1} % 隐层到输出层的阈值
%figure;
%plot(t);
%hold on;
%plot(y,'r:');
%legend('real','estimate');
%title('fitting curve');
%xlabel('sample points');
%ylabel('Passenger car ownership');
E=t-y;
ysse=sse(E);
ymse=mse(E);
hold off;
% figure
% plot(1:Count,E);
%polyfit(1:Count, E,3);
p1=m_data(Count+1:79,1:13);
t1=m_data(Count+1:79,14);
p=p1';t=t1';
%plot(t);
y=sim(net,p)
t
figure
plot(t);
hold on;
plot(y,'r:');
legend('real','estimate');
title('final fitting curve');
xlabel('sample points');
ylabel('Biodiversity');
%y*(4500.3924-81.62)+81.6
%E=t-y;
%ysse=sse(E);
%ymse=mse(E);