最短编辑问题也是一种非常经典的二维线性dp问题。

 

最短编辑问题也是一种非常经典的二维线性dp问题。

---

提示：以下是本篇文章正文内容，下面案例可供参考

一、最短编辑距离问题

给定两个字符串A和B，现将字符串A转换成字符串B至少进行多少次操作？

可进行的操作如下：

1. 删除–将字符串 A 中的某个字符删除。
2. 插入–在字符串 A 的某个位置插入某个字符。
3. 替换–将字符串 A 中的某个字符替换为另一个字符。

字符串中均只包含大小写字母 。

二、算法思路

1.dp[i][j]的情况

我们引入字符数组a来存储字符串A，字符数组b来存储字符串B。

引入二维dp数组，dp[i][j]表示字符串A的前i个字符变成字符串B的前j个字符所需要的最小操作数。

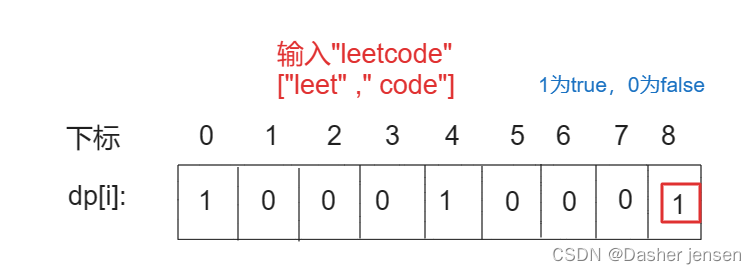
图1.1思路模拟

 由题意可知，我们如果想把字符串A变成字符串B，讨论字符串A的前i个和字符串B的前j个，即讨论dp[i][j]的值： 

• 增加一个字符：此时说明字符串A的前i个字符跟字符串B的前j-1个字符相等

 

• 删除一个字符：此时说明字符串A的前i-1个字符跟字符串B的前j个字符相等

 

•  替换一个字符：此时说明字符串A的前i-1个字符跟字符串B的前j-1相等

 

• 无操作，此时说明字符串A的第i个字符和字符串B的第j个字符是相等的，那么直接取dp[i-1][j-1]的值即可 

 

最后我们需要直到最少操作数，那么我们就需要在上述情况中找到最小值。

 2.边界问题初始化

我们需要考虑当dp[i][j]中i为0的情况或者j为0的情况：

• 当i为0的情况，此时说明字符串A为空，那么字符串A想要变成字符串B就只能通过增加操作。

 

 

• 当j为0的情况，此时说明字符串B为 空，那么字符串A想要变成字符串B只能进行删除操作

 

 

3.状态转移方程

删除和添加操作：

 

当a[i] != b[j]时，替换操作：

 

当a[i] = b[j]，不进行操作：

 

三、代码如下

1.代码如下

import java.io.*;
import java.util.Scanner;

public class 最短编辑距离 {
    static PrintWriter pw = new PrintWriter(new OutputStreamWriter(System.out));
    public static void main(String[] args) {
        Scanner sc = new Scanner(new BufferedReader(new InputStreamReader(System.in)));
        int n = sc.nextInt();
        String a = sc.next();
        int m = sc.nextInt();
        String b = sc.next();
        char[] Achar = new char[1010];
        char[] Bchar = new char[1010];
        for (int i = 1; i <= n; i++) {
            Achar[i] = a.charAt(i-1);
        }
        for (int i = 1; i <= m ; i++) {
            Bchar[i] = b.charAt(i-1);
        }
        int[][] dp = new int[1010][1010];
        //表示字符串B为空，那么字符串A的前i个字符变成字符串只进行删除操作
        //有多少个字符就进行多少次删除操作
        for(int i = 1; i <= n;i++){
            dp[i][0] = i;
        }
        //表示字符串A为空，字符串B的长度为i
        //那么把字符串A变成字符产B只能进行添加操作
        for(int i = 1;i <= m;i++){
            dp[0][i] = i;
        }
        for(int i = 1;i <= n;i++){
            for(int j = 1;j <= m;j++){
                dp[i][j] = Math.min(dp[i][j-1],dp[i-1][j])+1;
                if(Achar[i] != Bchar[j]){
                    dp[i][j] = Math.min(dp[i][j],dp[i-1][j-1]+1);
                }else {
                    dp[i][j] = Math.min(dp[i][j],dp[i-1][j-1]);
                }
            }
        }
        pw.println(dp[n][m]);
        pw.flush();
    }
}

2.读入数据

10 
AGTCTGACGC
11 
AGTAAGTAGGC

3.代码运行结果

4

 

---

总结

最短编辑问题我们需要知道dp[i][j]中i和j分别表示的含义，以及知道状态转移方程是如何推导出来的即可。